ブートストラップ法とは、取得できたサンプルデータが少ないときに、統計的な分析をするのに全然データが足りない場合に使用できる方法になる。
その少ないデータの中に外れ値と呼ばれるようなデータが含まれている場合は、そのデータがブートストラップ法によって算出される可能性が高くなるので、そうなる場合は処理を除くなどの必要性が高まる。
ここではそんなブートストラップ法について簡単に説明をしていこうと思います。
ブートストラップ法とは
取得したデータから、平均の分布を構築していくイメージになります。
真の分布(真の事象)からよく出るデータ(確率変数)は、
もちろん採れたデータにもよく含まれるはずなので、
その後そのデータに対してのブートストラップ処理をかましても、結局よく出るよねということになる。
簡単にブートストラップについて具体的なデータを用いて説明します。
例として取れたデータを、
1,1,2,2,2,3,3,3,3,3,3,4,4,4,5の15個とします。(あくまで例なのでめちゃ少ないですが、、)
このデータを分布にしてみると、3が多いので、3あたりが平均値としてはあり得そうなグラフができますね!
(ただ偶然15個とったらこういうデータが取れて、本当は20とかがめちゃくちゃ確率的には出るのかもですが、それは今回置いておきます。数増やせばいいだけなので。)
ここで真の平均を考えていきたいと思います。
そして上で取れたデータ15個からランダムでサンプリングをしていきます。
袋に上の15個の数字が入ったと見立てて、そこから値を取ると、当然ながら3が一番多いので、3が出やすいです。
それを同じように15回くらい復元でサンプリングしていくと、
1,1,1,2,2,2,3,3,3,3,4,4,4,5,5の15個取れたとします。
これがいわゆるブートストラップになります。
元々取れたデータに対してサンプリングをしていく手法になります。
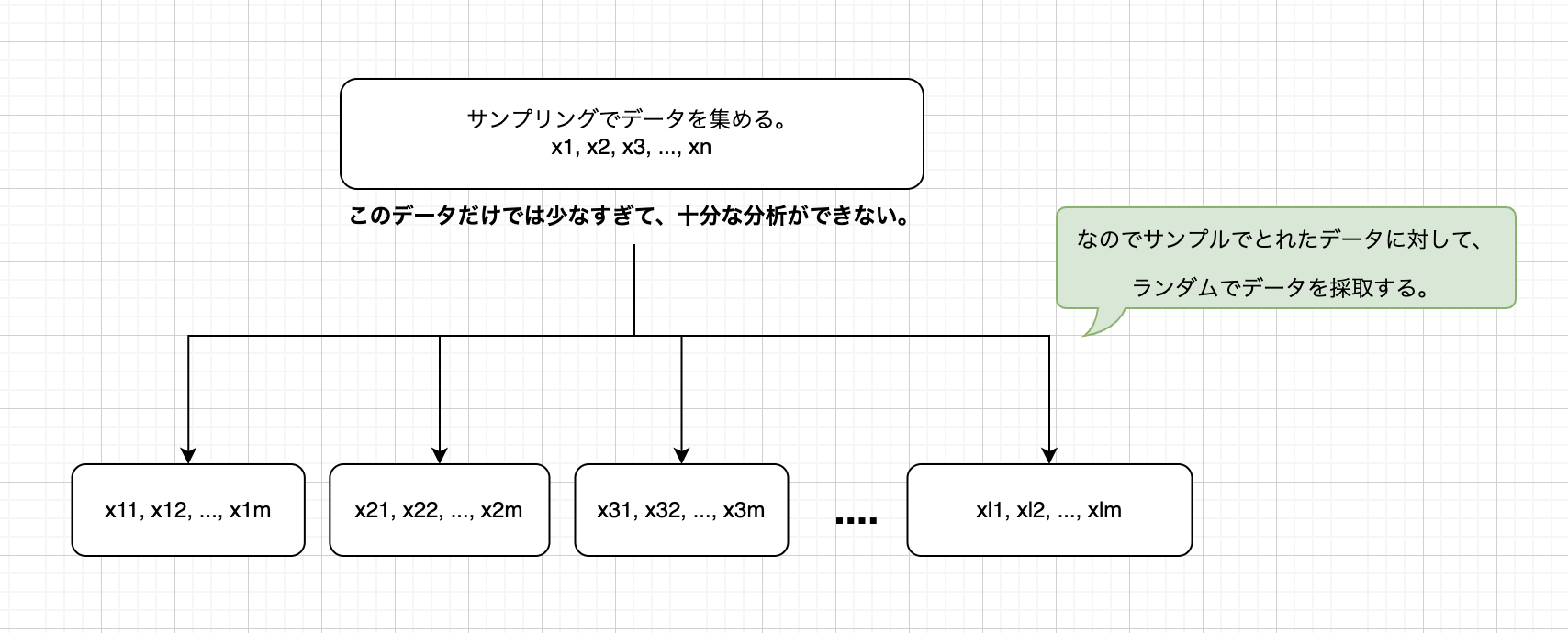
図にしてみると以下のような感じです。
取れたデータが15個でこれだけだと流石に予測や分析に使用できないので、ここからさらに復元サンプリングを行います。
同じ\(n\)=15でそれを何セットも繰り返しサンプリングをします。
ここで取れたデータをブートストラップ標本と言ったりします。
袋に入れたデータからサンプリングをするイメージになるので、最初に取れたデータで今回は2がすごい多いですが、袋から取り出す際ももちろん2が多く出るのは容易に想像できるかと思います。
出るべき値は、ブートストラップ標本でも出るってことですね!
今回のイメージでは説明上標本データは少ないですが、この数ですと実際2はあまり出ないのに偶然めちゃくちゃ取れてしまったり、逆に確率変数は1から8まで出るのに、取れたデータは1から5のみで、それ以外はもう取れないみたいなことにもなりますので、ブートストラップ法を使用する際は注意が必要になります。
イメージは分かりましたでしょうか?
これを実際に理論的に考えていきたいと思います。
ブートストラップ法を理論的に捉える
まず得られたデータを\( {\lbrace x_{i} \rbrace}_{i=1,2,...,n} \)とします。\(・・・①\)
ここから仮の真の平均(標本平均)を出すと、\(\theta = \displaystyle \frac{1}{n} \sum_{i=1}^{n} x_{i}\)となります。
そして次にブートストラップ処理を行います。
1回目で\(①\)から\(n\)回サンプリングを行い、取れたデータを\( {\lbrace x_{1i} \rbrace}_{i=1,2,...,n} \)とします。そしてこのデータからの平均値を\(\theta_{1}\)とします。
2回目で\(①\)から\(n\)回サンプリングを行い、取れたデータを\( {\lbrace x_{2i} \rbrace}_{i=1,2,...,n} \)とします。そしてこのデータからの平均値を\(\theta_{2}\)とします。
3回目で\(①\)から\(n\)回サンプリングを行い、取れたデータを\( {\lbrace x_{3i} \rbrace}_{i=1,2,...,n} \)とします。そしてこのデータからの平均値を\(\theta_{3}\)とします。
...
を繰り返し行っていき、
\(m\)回目で\(①\)から\(n\)回サンプリングを行い、取れたデータを\( {\lbrace x_{mi} \rbrace}_{i=1,2,...,n} \)とします。そしてこのデータからの平均値を\(\theta_{m}\)とします。
これを各上記のブートストラップ法によるリサンプリング結果のデータを用いて
\(\theta_{1}\), \(\theta_{2}\), \(\theta_{3}\), ..., \(\theta_{m}\)の\(m\)個のブートストラップ平均値が取得できました。
これで標本平均の分布図が書けそうですね!
ブートストラップ標本から得られた各種平均\( {\lbrace \theta_{i} \rbrace}_{i=1,2,...,m} \)を小さい順に並び替えます。
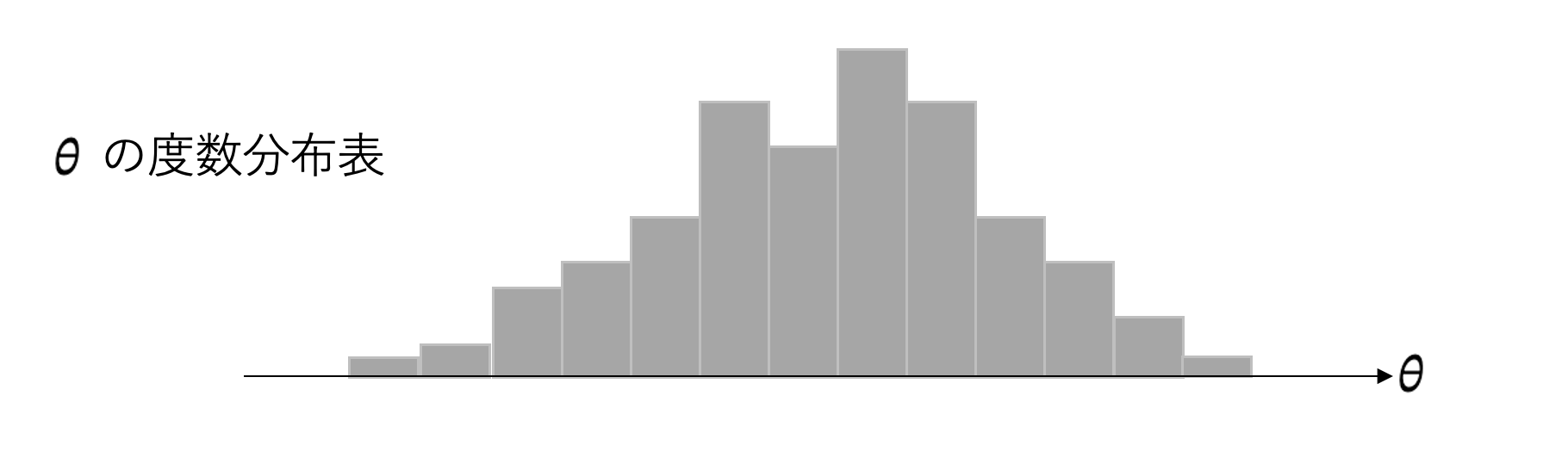
ブートストラップ標本の分布
上でとれた\(\theta_{m}\)の値を度数分布表に書いてみます。以下は例でイメージです。
\(\theta_{m}\)は様々な値を取りうるので確率変数になり、それ自体値ごとに確率が定義されます。
そのため、この分布表に曲線を通せば確率密度関数を出すことができますし、さらには分布関数も導くこともできます。
ここまで来れば、もうあとは普通の統計学の分野ですね!様々な処理をして分析したり、最尤法でパラメータを求めたり、、!
ブートストラップ標本の信頼区間
上で考えた標本平均のブートストラップ法で信頼区間の構築を考えてみます。
標本平均の分布を上で書いてみましたが、標本平均の分布は中心極限定理によって、正規分布に収束することが知られています。
そのため、普段僕らが考えている信頼区間のような考え方で信頼区間の構築が可能ということになります。
各種の平均{\(\theta_{i (i=1,2,3,...m}\)}は互いに独立な関係なので(それぞれの結果に影響を与えていない)、
標本平均の期待値E\([\bar{X}]\)は、
\begin{eqnarray}
E[\bar{X}]
&=& E \left[ \frac{1}{n}{\displaystyle \sum_{i=1}^{m} \theta_{i}} \right] \\
&=& \frac{1}{n} { E[\theta_{1}]+E[\theta_{2}]+E[\theta_{3}] + \cdot + \cdot + \cdot + E[\theta_{m}] } \\
\end{eqnarray}
ブートストラップ法
経験分布を作成して、小さい順にサンプリングされたデータを並び替えます。
そして有意水準5%として、上側限界区間とした時、
並び替えたデータでの上から5%分のデータを除いた範囲を構築することで、
信頼区間の構築を行うことが可能となります。
標本データで取得できたデータが\(n\)個だったとする。
ブートストラップ法では例えデータがかぶってたとしても、それらは固有もの(区別する)として復元サンプリングを行います。
これにより、それぞれのデータを取得する確率は等分の\(\displaystyle \frac{1}{n}\)になります。
そして信頼区間の構築では、単純に得られたデータに対して、
取得したデータの小さい順に並び替えます。
そして例えば、50組のデータストラップ標本の平均値をサンプリングしたのであれば、その50個を小さい順に並び替えます。
今回有意水準を上限10%とした時、
上から5個が、有意水準に該当してしまうので、その5個が含まれるギリギリの値で平均値を構築します。
これによって信頼区間の構築が可能になります。
ブートストラップ法の要注意ポイント
少ないデータだからと全ての取得できたデータを用いるのではなく、これは普通あり得ない数値だなとか、疑わしき値があればそれは除くなどのデータクレンジングをした上で、ブートストラップ法を行う必要があります。
やる場合は外れ値も考える必要があるので、外れ値は必ず左か右かになるので、極端に値が大きい、かけ離れているものがあれば、それを除くのは1つの手段かなと思います。
少ないデータの中に外れ値が混ざってしまっていると、その数値がブートストラップを行った後かなり外れ値が紛れ込んだ平均となってしまうので、要注意です。
そして求めた平均値を小さい順にならべることで、分布関数を導くことも可能になります。
分布関数と確率密度関数は1対1なので、分布関数が求まってしまえば、平均の確率密度関数(正式には連続ではないので、確率関数)を求めることもできます。