わかりやすいフィッシャー情報量

ここでは最尤推定量によるさまざまな性質について考えていきたいと思います。
その中でも以下の内容を扱っていきます。

• フィッシャー情報量
• スコア関数・エフィシェントスコア
• クラメール・ラオの不等式
• 最尤推定量の漸近分布

最尤法の知識がある前提なので、もし最尤法が何かわからないということでしたら、以下で扱っているのでぜひ一読していただければと思います。
最尤法

そもそもフィッシャー情報量とは

フィッシャー情報量の定義とは、確率変数\(X\)が母数\(\theta\)に関して持つ「情報」の量を表す。
これはどういうことか？
実際にフィッシャー情報量の定義式から考えてみましょう。
まず\(f(x|\theta)\)という確率密度関数を定義します。
さらに尤度を考えると、尤度\(l(\theta|x)\)は、式の形式から、\(x\)を条件付きにして、得られた\(\theta\)となります。
よって、ここで\(x\)から\(\theta\)が得られるという構図ができ、これで\(x\)→\(\theta\)ができた。
ただこれだけだと計算が難しいので、最尤法と同じように対数を取ります。
尤度は常に0よりも大きいので、対数を取ることができます。

そして対数尤度関数に対して偏微分したものをスコア関数と言います。

簡単に説明をすると、
尤度関数はデータ\(x\)が取得できた時の確率分布として定めて、
\(L(\theta|x)\)
とかけるので、データ\(x\)が得られた時の\(\theta\)の確率分布と言い換えることができる。
ということは、\(\theta\)を出すために必要な\(x\)がもつ情報量を考えよう！
エントロピーの概念で、そもそも滅多に出ない情報が出るとそれは情報としてはすごいいいものである。
それを確率分布的に表現すると、\(y\)軸に凸しているイメージ。
そして何も情報がないものとしては全てが均一に確率がある場合、つまり一様分布のようなイメージ。
これって常に傾きが0のイメージ。

ということは情報量の大きさは尤度関数の傾きに比例すると表現でき、
傾きはマイナスを取ることもあるので2乗にして、以下で定義をすることができる。

フィッシャー情報量は確率変数を\(x\)とした時、\(x\)がパラメータ\(\theta\)に対して持つ情報量のことです。
情報量という言葉は、、、、、で扱われることが多い。
情報量という言葉の定義は難しいが、

wikiから
尤度関数（ゆうどかんすう、英: likelihood function）とは統計学において、ある前提条件に従って結果が出現する場合に、逆に観察結果からみて前提条件が「何々であった」と推測する尤もらしさ（もっともらしさ）を表す数値を、「何々」を変数とする関数として捉えたものである。 また単に尤度ともいう。
と記載がある。
結果、つまり得られたデータ\(x\)から、特定の確率密度関数を求めるとなったときに、その得られたデータxからその密度関数のパラメータを最尤法によって求めます。
ということはその\(x\)から\(\theta\)を出すにあたってどのくらい情報を持っているか、どのくらい尤もらしいかを考えるのがこのフィッシャー情報量ということになります。
どのくらい尤もらしいかを出すには当然ながら、算出するパラメータの分布が分散が小さい（めちゃ上に凸みたいな感じ。）感じになれば、ものすごくそのパラメータ値が妥当になる。
逆に横に平べったいパラメータ分布(尤度関数）となる場合、どのパラメータもあり得るという感じになり、最もらしさが失われる。
このとき各パラメータの傾きはほぼ同じになる。（そして平べったいので0に近しい）

これらのことから、尤度関数の傾きが大きければ上に凸になり、最もらしく分散が小さいパラメータ分布になっているので、これ！っていうパラメータ値がもとまる。→つまり情報量が大きい

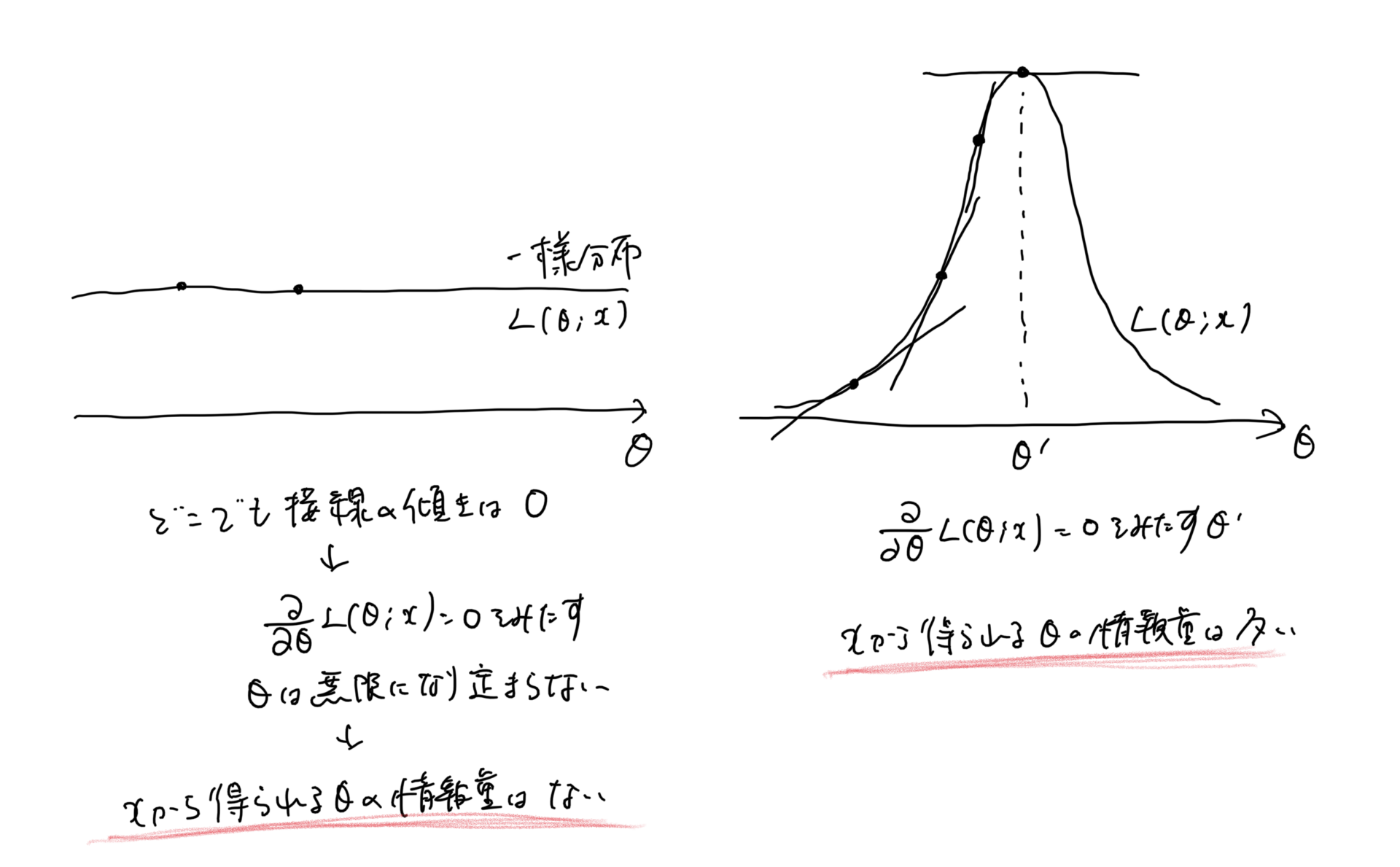
傾きが小さければ平べったくなり、どのパラメータでもあり得てしまうので尤もらしさがなく分散が大きいパラメータ分布になっているので、これ！っていうものがない。→ つまりxの情報量が小さい
よって、
\begin{eqnarray}
I(\theta) &=& E \left[ \left( \frac {\partial \log{f_{\theta}(y)}} {\partial \theta} \right)^{2} \right]
\end{eqnarray}
と定義ができる。
（こう解釈するとこのフィッシャー情報量の定義式が覚えやすくなる気がする、、）

つまり内容としては、
パラメータの分散⇄フィッシャー情報量の大きさ
になるということになる。

尤度の対数とって、微分ということは微分つまり接線の傾き（前後の変化率）が大きければ大きいほど、
尤度関数が凹凸になり、それは情報量が大きくなることと同値になる。
情報量がマイナスになることは基本的にない？ため、

これによって次に分散の大きさを定義する。

スコア関数・エフィシェントスコア

スコア関数とは尤度関数をパラメータで偏微分したもののことを言います。
最尤法で計算するとき、尤度関数を直接偏微分してもなかなか計算ができない場合があるので、対数をとった対数尤度関数に対して偏微分を行うことが通常ではあるが、
今回は対数取る以前の尤度関数に対して偏微分したものを扱います。

スコア関数の期待値

このスコア関数\(U(\theta; x)\)の期待値を求める。
合成関数の微分法により
\begin{eqnarray}
L(\theta; x) &=& f(x; \theta) \\
U(\theta; x)
&=& \frac{ \partial }{\partial \theta} {\log L(\theta; x)} \\
&=& \frac{1}{L(\theta; x)} \frac{ \partial }{\partial \theta} {L(\theta; x)} \\
\end{eqnarray}

よって期待値をとって、
\(L(\theta;x) = f(x; \theta)\)ということと、積分と微分の交換（正則条件を仮定）ができると想定して、
\begin{eqnarray}
E_{f}[U(\theta; x)]
&=& \int_{-\infty}^{\infty} U(\theta; x)f(x ; \theta) dx \\
&=& \int_{-\infty}^{\infty} \frac{1}{L(\theta; x)} \frac{ \partial }{\partial \theta} {L(\theta; x)}f(x ; \theta) dx \\
&=& \int_{-\infty}^{\infty} \frac{ \partial }{\partial \theta} {L(\theta; x)} dx \\
&=& \frac{\partial}{\partial \theta}　\int_{-\infty}^{\infty} {L(\theta; x)} dx \\
&=& \frac{\partial}{\partial \theta}　\int_{-\infty}^{\infty} {f(x;\theta)} dx \\
&=& \frac{\partial}{\partial \theta}　1 \\
&=& 0
\end{eqnarray}
よって、
\(E_{f}[U(\theta; x)] = 0\)
となる。

スコア関数の分散

分散公式を使うと、まさにスコア関数\(U(\theta, x)\)の分散はフィッシャー情報量と一緒になる。
分散公式と上の期待値の結果から、
\begin{eqnarray}
V_{f}(U(\theta; x))
&=& E[U(\theta; x)^{2}] + {E[U(\theta; x)]}^{2} \\
&=& E[U(\theta; x)^{2}] \\
\end{eqnarray}

フィッシャー情報量の書き換え

フィッシャー情報量の定義式を書き換えてみます。(次の最尤推定量の漸近分布の導出に使用します）
合成関数の微分法と積の微分法を使用して、
\begin{eqnarray}
\frac{\partial^{2}}{\partial \theta^{2}}{\log L(\theta; x)}
&=& \frac{\partial}{\partial \theta} \left\{\frac{\partial}{\partial \theta}{\log L(\theta; x)} \right\} \\
&=& \frac{\partial}{\partial \theta} \left\{ \frac{1}{L(\theta; x)} \frac{\partial}{\partial \theta}{L(\theta; x)} \right\} \\
&=& \left\{\frac{\partial}{\partial \theta} \frac{1}{L(\theta; x)} \right\} \cdot \frac{\partial}{\partial \theta}{L(\theta; x)} + \frac{1}{L(\theta; x)} \cdot
\left\{ \frac{\partial^{2}}{\partial \theta^{2}}{L(\theta; x)} \right\} \\
&=& -\frac{1}{L(\theta; x)^{2}} \frac{\partial}{\partial \theta}{L(\theta; x)} \cdot \frac{\partial}{\partial \theta}{L(\theta; x)} + \frac{1}{L(\theta; x)} \cdot \frac{\partial^{2}}{\partial \theta^{2}}{L(\theta; x)} \\
&=& -\frac{1}{L(\theta; x)^{2}} \left\{\frac{\partial}{\partial \theta}{L(\theta; x)} \right\}^{2} + \frac{\partial}{\partial \theta} \frac{1}{L(\theta; x)} \cdot \frac{\partial}{\partial \theta}{L(\theta; x)} \\
&=& - \left\{ \frac{1}{L(\theta; x)} \frac{\partial}{\partial \theta}{L(\theta; x)} \right\}^{2} + \frac{\partial}{\partial \theta}{\log L(\theta; x)} \\
&=& - \left\{ \frac{\partial}{\partial \theta}{\log L(\theta; x)} \right\}^{2} + \frac{\partial}{\partial \theta}{\log L(\theta; x)} \\
\end{eqnarray}

これに対して、期待値をとると、
\begin{eqnarray}
E \left[\frac{\partial^{2}}{\partial \theta^{2}}{\log L(\theta; x)} \right]
&=& E \left[ - \left\{ \frac{\partial}{\partial \theta}{\log L(\theta; x)} \right\}^{2} + \frac{\partial}{\partial \theta}{\log L(\theta; x)} \right]\\
&=& -E \left[\left\{ \frac{\partial}{\partial \theta}{\log L(\theta; x)} \right\}^{2} \right] + E \left[\frac{\partial}{\partial \theta}{\log L(\theta; x)} \right]\\
\end{eqnarray}

右辺の第2項はまさに、スコア関数の期待値となるので0となり、
\begin{eqnarray}
E \left[\frac{\partial^{2}}{\partial \theta^{2}}{\log L(\theta; x)} \right]
&=& -E \left[\left\{ \frac{\partial}{\partial \theta}{\log L(\theta; x)} \right\}^{2} \right]
\end{eqnarray}

となるので、フィッシャー情報量は以下のように書き換えることが可能になります。

\begin{eqnarray}
I(\theta) = E \left[\left\{ \frac{\partial}{\partial \theta}{\log L(\theta; x)} \right\}^{2} \right] = -E \left[\frac{\partial^{2}}{\partial \theta^{2}}{\log L(\theta; x)} \right]
\end{eqnarray}

クラメール・ラオの不等式

これがクラメールの不等式がある。

\begin{eqnarray}
V(\hat{\theta_{}}) \geq \frac{1}{I(\theta)}
\end{eqnarray}

分散の一番低い値を算出するための不等式です。
ある平均が出ている時に、この分散がどのくらい低い値を出すかを不等式で算出するものです。
これにより、当然データや統計量、パラメータの確率変数の値が分散していなければいないほど、この値に収束するなどのことが得られ、パラメータの値としてはこの値に収束しそうと断定できる。

最尤推定量の漸近分布

ここでは最尤法の知識がある前提で話します。
最尤法を知らない方は以下でも扱ってるので、ぜひ。
最尤法
ここで確率密度関数を\(f(x|\theta)\)とします。
そして確率変数を\(x_{i} i=1,2..,n\)とします。
このとき尤度関数\(L(\theta|x)\)は、
\begin{eqnarray}
L(\theta|x) = \prod_{i=1}^n {f(x_{i}|\theta)}
\end{eqnarray}
対数尤度関数\(l(\theta|x)\)は
\begin{eqnarray}
l(\theta|x)
&=& \log(L(\theta|x)) \\
&=& \sum_{i=1}^{n} \log(f(x_{i}|\theta)) \\
\end{eqnarray}
となる。この仮定のこと、最尤推定量の漸近分布を出してみたいと思います。
まず最尤法を求める感じで、あるパラメータ部分して=0とします。
まず対数尤度関数をパラメータで微分して=0とする
\begin{eqnarray}
\frac {\partial \log{L(\theta|x)}} {\partial \theta} \equiv 0
\end{eqnarray}
そしてここで左辺の式に対してマクローリン展開(テイラー展開の中心点を0)すると、ここでもとまる最尤推定量\(\hat{\theta_{}}\)として、

テイラー展開をすると、対数尤度関数をパラメータで偏微分して=0により、
\begin{eqnarray}
\frac {\partial \log{l(\theta|x)}} {\partial \theta} &\equiv& 0
\end{eqnarray}
となり、これに対してテイラー展開をすると、
\begin{eqnarray}
\frac {\partial \log{L(\theta|x)}} {\partial \theta} \cdot \frac{(\theta - \theta_{0})^{0}}{0!} + \frac {\partial^{2} \log{L(\theta|x)}}{\partial \theta^{2}} \cdot \frac{(\theta - \theta_{0})^{1}}{1!} &\equiv& 0 \\
\frac {\partial \log{L(\theta|x)}} {\partial \theta} + \frac {\partial^{2} \log{L(\theta|x)}}{\partial \theta^{2}} \cdot (\theta - \theta_{0}) &\equiv& 0 ・・・① \\
\end{eqnarray}
となります。

\(n \rightarrow \infty\)を取り、第1項、第2項について考えます。

第1項目について

ここで\(①\)の第1項は\(n \rightarrow \infty\)によって、標準正規分布に収束することがわかり、
以下が成立することにより、
ここで\(\displaystyle z_{i} = \frac {\partial \log{L(\theta|x_{i})}} {\partial \theta} \)とした時、
\begin{eqnarray}
E \left[ z_{i} \right] &=& 0 \\
V \left( z_{i} \right) &=& I(\theta) \\
\end{eqnarray}
\begin{eqnarray}
Z_{i}
&=& \frac{z_{i} - E[z_{i}]}{\sqrt{V(z_{i})}} \\
&=& \frac{z_{i}}{\sqrt{I(\theta)}}
\end{eqnarray}
となり、標準化することができる。

第2項目について

こちらは大数の法則を考えます。

ここで\(\displaystyle w_{i} = \frac {\partial^{2} \log{L(\theta|x_{i})}} {\partial \theta^{2}} \)とした時、
\(\displaystyle \frac{1}{n}\sum_{i=1}^{n}{w_{i}}\)は純粋にnで割り、大数の法則により、期待値に確率収束します。
つまり、
\(E[w_{i}]\)に確率収束します。
そのため、\(①\)の第2項は、本ページの「フィッシャー情報量の書き換え」の結果を用いて、
\begin{eqnarray}
E[w_{i}]
&=& E \left[ \frac {\partial^{2} \log{L(\theta|x_{i})}} {\partial \theta^{2}} \right] \\
&=& -I(\theta) \\
\end{eqnarray}
となります。

第1項、第2項を計算すると、

\begin{eqnarray}
W_{i}
&=& \frac{z_{i} - E[z_{i}]}{\sqrt{V(z_{i})}} \\
&=& \frac{z_{i}}{\sqrt{I(\theta)}}
\end{eqnarray}

\begin{eqnarray}
\sqrt{n}(\hat{\theta_{}}-\theta_{0}) \sim \frac{u}{I_{1}(\theta_{0})}
\end{eqnarray}

対数尤度関数に対して

まず100個データをとったとします。
そして図を書いて、こんな分布かーって見ます。
そして次にまた100個サンプリングします
そして図を書いて、こんな分布かー
そしてまた100個、こんな分布かー
って見ます
そうするとやはりよく出る確率変数はよくサンプリングされるし、
あまり出ないものはやはりあまり出ない感じになると思いますが、
毎回毎回同じデータが出るわけではないので、
今100個のデータを3セット作成して、それぞれで最尤推定量を求めても、値が違かったりします。

これでパラメータの値を新しい確率変数として分布を取ると尤度関数が出来上がります。
100ではなく、100000個とかにすると、100個ではまぐれで滅多に出ないものが多く出てしまったりしたが、より精緻になり、出ないものはより出なくなるようになるので、
また同じように100000個3セット作って再度パラメータの分布を作って最尤推定値を求めるとかなり近しい値になると思います。
それを3セットでなく何セットもやって分布を作ると、結構1つの値の周りに集中するような感じになるかなと思います。
まさに分散が小さくなっていて、尤度関数がピーーんと上に凸の状態の関数になる感じになります。

最尤推定量の信頼区間

パラメータ最尤推定量の分布は上で
\begin{eqnarray}
\sqrt{n}(\hat\theta-\theta_{0}) \sim \frac{u}{I_{1}(\theta_{0})}
\end{eqnarray}
と求まりました。
この式から構築していきましょう。
最尤推定量をもつパラメータ\(\theta\)は、クラメール・ラオの不等式により、正規分布\(N(\theta_{0}, \displaystyle \frac{1}{nI_{1}(\theta_{0}) }) \)に従うので、以下のように標準化できる。
\begin{eqnarray}
Z
&=& \frac{\theta - E[\theta]} { \sqrt{V(\theta) })} \\
&=& \frac{\theta - \theta_{0}}{\displaystyle \sqrt{ \frac{1}{nI_{1}(\theta_{0})} }} \\
&=& \sqrt{nI_{1}(\theta_{0}) } ({\theta - \theta_{0}})
\end{eqnarray}

従って、\(Z\)は標準正規分布\(N(0,1)\)に従うので、片側検定として有意水準\(\alpha\)％としたとき、信頼区間は\(P(Z) \geq 1-\alpha \)より、
\begin{eqnarray}
\sqrt{nI_{1}(\theta_{0}) } ({\theta - \theta_{0}}) \geq z_{\alpha}
\end{eqnarray}
となる。