
サンプリングを考える場合は、
復元と非復元を考える必要があります。
さらに言えば復元の場合は、毎回全てのデータがある状態でサンプリングなので、1個前にサンプリングしたデータがどんなものであれ、毎回全てが候補になります。
しかし、非復元の場合は、1回取ったものは元に戻さないので、だんだんとあるデータの出る確率が相対的に上がっていきます。そりゃそうですよね。なので、この場合は1個前だけではなく過去に取ったデータに影響を受けているので、独立ではありません。
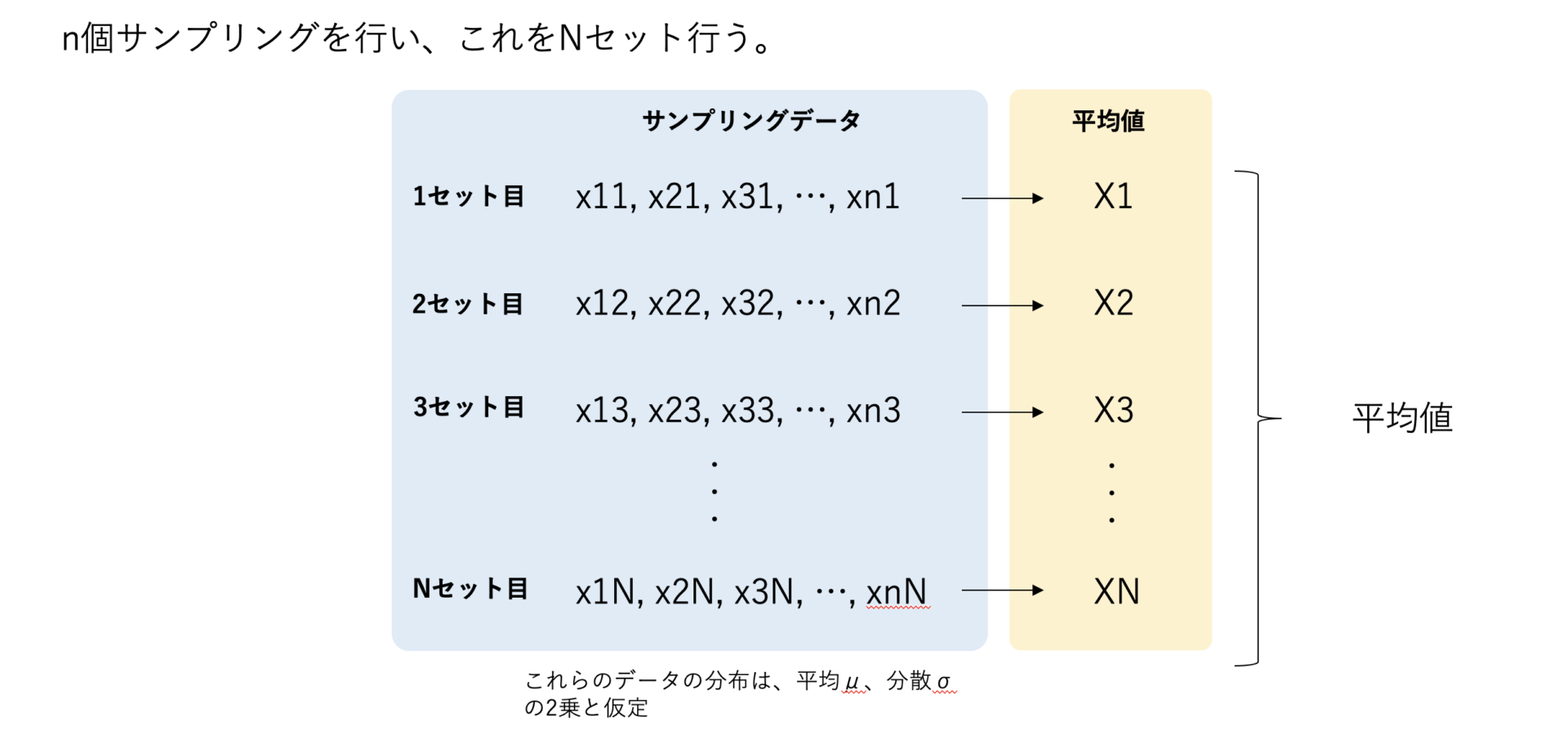
ただ単純にサンプリングをすることは簡単ですが、サンプリングをする対象のことを考えた上で設計をしないとデータとして不整合のものとなってしまいます。
例えば以下のようにアンケートデータを想定してみましょう。
1人の回答を何回も使うことはない。1人回答もらったら、残りのN-1人から回答をもらいます。
なので、サンプリングをする際は、このように独立ではないことの方が多い。つまり復元ではなく非復元を想定したサンプリングとなる。
すなわち、基本的には上記のような考え方で標本平均の期待値と分散を求めることに帰着される。
問題提起だけ、入りだけは違うけど、結局計算をする方法については同じ。
アンケートの場合は、同じ人に何回も回答を求めることはしません。
つまり、非復元です。
単純に正規表現からサンプリングをすることと、人からアンケートをとることは全く手法などが異なるわけです。
このように、復元・非復元を考える必要があります。
ココがポイント
サンプリングをする際はこれは復元なのか非復元なのか、母集団は有限なのか無限なのかを考えてサンプリングを行う。
Contents
期待値
復元の単純サンプリング
通常の無作為サンプリングを考えたとき、
例えば出たデータを\(X_{i}\)とし、\(E[X_{i}] = \mu\)として、確率変数\(X_{i}\)は互いに独立としたとします。
通常は、反復(復元)であれば、各確率変数は独立した状態なので、
\begin{eqnarray}
E[\bar{X_{}}]
&=& E[\sum_{i=1}^{n} X_{i}] \\
&=& \frac{1}{n} \{ E[X_{1}]+E[X_{2}]+\cdot\cdot\cdot +E[X_{n}] \} \\
&=& \frac{1}{n} \{ \mu+\mu+\cdot\cdot\cdot +\mu \} \\
&=& \frac{1}{n} \cdot n\mu \\
&=& \mu \\
\end{eqnarray}
\(E[\bar{X_{}}] = \mu\)がわかり、
標本平均の期待値\(E[\bar{X}]\)は独立なので単純に対して計算をすることが可能になります。
非復元の単純サンプリング
しかし、これが反復(非復元)だった場合、どうでしょうか?
非復元ということは独立ではないです。前に引いたデータはもう引くことがないので、確率はちょっと出やすくなります。つまり可能性が上がるので前の結果の影響を受けてると言えるでしょう。
そのため、独立の時のような単純に対して計算をするということができなくなります。つまり、
標本平均の期待値は普通に以下のように計算ができないということです。
\(E[\bar{X_{}}] = E[X_{1}] + E[X_{2}] + ... + E[X_{n}]\)
ではどうするか?
標本平均はそもそも統計量です。そして取れたデータに対して計算をすることで、1つの確率変数となります。
さらにまた同じようにサンプリングをして、標本平均を求めると、これも1つの確率変数となります。
このように標本平均は確率変数になるので、これを逆手にとって、確率で計算しようということです。
期待値の定義は、以下の計算です。確率変数ごとの確率の積をします。
\(E[X] = \sum_{i=1}^{m} xP(X = x) \)
上の独立の時のように簡単に標本平均に対して期待値をとって足してってことができないので、
ここはちゃんと標本平均を確率変数とみなして、期待値の定義に遡って計算をしていきましょう!
ココがポイント
非復元の場合は、標本平均を確率変数と見立てて、期待値の定義から計算をする。
これを標本平均のようにして計算を定義してみます。
\(E[\bar{X_{}}] = \sum_{i=1}^{m} \bar{X_{i}}P(X = \bar{X_{i}}) \)
ここでは、標本平均を出すのに、各データはn個、そしてそれによって作成された標本平均(確率変数)の個数はm個とします。
まず1個取得して、残り\(n-1\)個で、そこから1個とって残り\(n-2\)個で、そこからまた1個とって残り\(n-3\)で、、、繰り返しとっていき
\begin{eqnarray}
P(X = \bar{X_{i}})
&=& \frac{1}{N(N-1)(N-2)(N-3)...} \\
\end{eqnarray}
※ ちなみに、これはどの標本平均の値でも同じ一定の確率になります。
これにより、
\begin{eqnarray}
E[\bar{X_{}}]
&=& \sum_{i=1}^{n} \bar{X_{i}} P(X = \bar{X_{i}}) \\
&=& \sum_{i=1}^{n} \bar{X_{i}} \cdot \displaystyle \frac{1}{N(N-1)(N-2)(N-3)\cdot\cdot\cdot} \\
&=& \displaystyle \frac{1}{N(N-1)(N-2)(N-3)\cdot\cdot\cdot} \cdot \sum_{i=1}^{n} \frac{1}{n} \{x_{1}+x_{2}+...+x_{i} \} \\
\end{eqnarray}
順列を考えます。
1回の試行で\(n\)個をサンプリングするわけですが、その中でも順列を考えます。
ある変数を3回目に出たとしてそれを固定します。この時他の1,2,4,5,...,n回で取れるデータは
すでに1つ3回目の結果を固定していてそれ以外のN-1個から1つ、そして2回目はN-2個、、、とやっていくと、1回の試行における順列は(N-1)(N-2)...(N-n+1)通り。
そして3回目固定したものがあるので、それを他に1回目にしたり2回目にしたりとするパターンもあるので、n回をかけて、
n*(N-1)(N-2)...(N-n+1)通りとなる。
したがって、
\begin{eqnarray}
E[\bar{X_{}}]
&=& \frac{1}{N(N-1)(N-2)(N-3)\cdot\cdot\cdot} \cdot \sum_{i=1}^{n} \frac{1}{n} \{x_{1}+x_{2}+...+x_{i} \} \\
&=& \frac{1}{N(N-1)(N-2)(N-3)\cdot\cdot\cdot} \cdot \sum_{i=1}^{n} \frac{1}{n} \{x_{1}+x_{2}+...+x_{i} \} \\
\end{eqnarray}
分散
復元の単純サンプリング
分散も同様に通常確率変数が互いに独立であれば、簡単な単純な足し算で計算をすることが可能になります。
確率変数\(X_{i}\)について、\(E[X_{i}] = \mu\)、\(V(X_{i}) = \sigma^{2}\)と仮定したとき、(つまりこれらのデータの分布が平均\(\mu\)で分散が\(\sigma^{2}\)と仮定したとき)
\begin{eqnarray}
V(\bar{X})
&=& V(\frac{1}{n}\sum_{i=1}^{n} V(X_{i})) \\
&=& \displaystyle \frac{1}{n^{2}} \{V(X_{1}) + V(X_{2}) + ... + V(X_{n})\} \\
&=& \displaystyle \frac{1}{n^{2}} \cdot n\sigma^{2} \\
&=& \displaystyle \frac{\sigma^{2}}{n}
\end{eqnarray}
この「復元」の場合、例え母集団が有限だったとしても、復元なので何個もサンプリングが可能です。
例えば袋に入ったボール5個からサンプリングをするとなった時、1つとってまたそれを復元なので袋に戻すので、毎回5個の状態からサンプリングをすることになるので、永遠にサンプリングが可能になります。
そのため、先に結論を言うと有限Nとして仮定しても、Nを無限大にして復元しても同じ結果が得られます。
非復元の単純サンプリング
しかし独立ではない場合はこのような計算をすることができず、期待値の時と同様に定義から直接計算をすることになります。
上で標本平均の期待値は、\(\mu\)となったので、以下の計算をして導きます。
\begin{eqnarray}
V(\bar{X})
&=& E[(\bar{X}-E[\bar{X}])^{2}] \\
&=& E[(\bar{X}-\mu)^{2}] \\
&=& E[( \frac{1}{n} \sum_{i=1}^{n} X_{i} - \mu )^{2}] \\
&=& E[ \frac{1}{n^{2}} ( \sum_{i=1}^{n} X_{i} - n\mu )^{2}] \\
&=& \frac{1}{n^{2}}E[ ( X_{1}+X_{2}+\cdot\cdot\cdot+X_{n} - n\mu )^{2}] \\
&=& \frac{1}{n^{2}}E[ ( (X_{1}-\mu) + (X_{2}-\mu) + \cdot\cdot\cdot + (X_{n}-\mu) )^{2}] \\
&=& \frac{1}{n^{2}}E[ ( \sum_{i=1}^{n}(X_{i}-\mu)^{2} + \sum_{l \neq k}(X_{l}-\mu)(X_{k}-\mu)] \\
\end{eqnarray}
ここで、独立なので、
\begin{eqnarray}
V(\bar{X})
&=& \frac{1}{n^{2}} \{ E[\sum_{i=1}^{n}(X_{i}-\mu)^{2}] + E[\sum_{l \neq k}(X_{l}-\mu)(X_{k}-\mu)] \} \\
&=& \frac{1}{n^{2}} \{ \sum_{i=1}^{n} E[(X_{i}-\mu)^{2}] + \sum_{l \neq k}E[(X_{l}-\mu)(X_{k}-\mu)] \} \\
&=& \frac{1}{n^{2}} \{ n\sigma^{2} + \sum_{l \neq k}E[(X_{l}-\mu)(X_{k}-\mu)] \} ・・・※\\
\end{eqnarray}
ここで、\(E[(X_{l}-\mu)(X_{k}-\mu)]\)について考えます。
\(E[(X_{l}-\mu)(X_{k}-\mu)]\)の\(l\)と\(k\)の組み合わせは、\(l\)で4とした時、\(k\)は4以外となるので、\(N(N-1)\)通り。
そして確率は\(\frac{1}{N(N-1)}\)になります。
つまり、\(P(X_{1} = X_{l}, X_{2} = X_{k}) = \frac{1}{N(N-1)}\)となります。
したがって、確率変数のlとkの組み合わせは、N(N-1)通りなので、
\begin{eqnarray}
E[(X_{l}-\mu)(X_{k}-\mu)]
&=& \frac{1}{N(N-1)} \sum_{l \neq k} (X_{l}-\mu)(X_{k}-\mu) \\
\end{eqnarray}
ここで、
\(\sum_{l \neq k} (X_{l}-\mu)(X_{k}-\mu) = \{\sum (X_{l}-\mu) \}^{2} - \sum_{i=1}^{N} (X_{l}-\mu)^{2} \)であることから、
(全てのlとkの組み合わせから、同じlやkの組み合わせを除ければ、lとkの値が違う組み合わせのみ残ることを計算して。和集合から共通部分を除いたものがlとkの掛け算になってるっていうイメージ)
\begin{eqnarray}
E[(X_{l}-\mu)(X_{k}-\mu)]
&=& \frac{1}{N(N-1)} \sum_{l \neq k} (X_{l}-\mu)(X_{k}-\mu) \\
&=& \frac{1}{N(N-1)} [ \{\sum (X_{l}-\mu) \}^{2} - \sum_{i=1}^{N} (X_{l}-\mu)^{2} ] \\
\end{eqnarray}
\begin{eqnarray}
\{(X_{1}-\mu) + (X_{2}-\mu)\}^{2}
&=& (X_{1}-\mu)^{2} + (X_{1}-\mu)(X_{2}-\mu) + (X_{2}-\mu)^{2} \\
&=& \{(X_{1}-\mu)^{2} + (X_{2}-\mu)^{2}\} + (X_{1}-\mu)(X_{2}-\mu) \\
(X_{1}-\mu)(X_{2}-\mu) &=& \{(X_{1}-\mu) + (X_{2}-\mu)\}^{2} - \{(X_{1}-\mu)^{2} + (X_{2}-\mu)^{2}\} \\
\sum_{l \neq k}(X_{l}-\mu)(X_{k}-\mu) &=& \{ \sum (X_{l}-\mu) \}^{2} + \sum (X_{l}-\mu)^{2}
\end{eqnarray}
ここで、
\begin{eqnarray}
\sum (X_{l}-\mu)
&=& (X_{1}-\mu)+(X_{2}-\mu)+(X_{3}-\mu)+\cdot\cdot\cdot+(X_{N}-\mu) \\
&=& (X_{1}+X_{2}+X_{3}+\cdot\cdot\cdot+X_{N})-N\mu \\
&=& N\mu-N\mu \\
&=& 0
\end{eqnarray}
となるので、分散は変数と平均の距離の2乗の平均なので、
\begin{eqnarray}
E[(X_{l}-\mu)(X_{k}-\mu)]
&=& \frac{1}{N(N-1)} [ 0 - \sum_{i=1}^{N} (X_{l}-\mu)^{2} ] \\
&=& \displaystyle -\frac{\sum_{i=1}^{N} (X_{l}-\mu)^{2}}{N(N-1)}\\
&=& \displaystyle -\frac{N\sigma^{2}}{N(N-1)}\\
&=& \displaystyle -\frac{\sigma^{2}}{N-1}\\
\end{eqnarray}
したがって、※の第2項について、\(l\)と\(k\)の組み合わせは\(n(n-1)\)通りなので、
\begin{eqnarray}
V(\bar{X_{}})
&=& \frac{1}{n^{2}} \{ n\sigma^{2} \displaystyle -\frac{n(n-1)\sigma^{2}}{N-1} \}\\
&=& \displaystyle \frac{\sigma^{2}}{n}( 1 - \frac{n-1}{N-1})
\end{eqnarray}
これで、期待値と分散を求めることができました。
無限母集団の場合どうなるか?
今までは\(N\)として有限母集団を考えていきました。
なので、無限母集団を考えたい場合は、ただ\(N \rightarrow \infty\)を取れば良いです。
先程求めた期待値と分散に対して\(N \rightarrow \infty\)を適用すると、
\begin{eqnarray}
V(\bar{X_{}})
&=& \displaystyle \frac{\sigma^{2}}{n}( 1 - \frac{n-1}{N-1}) \\
&\rightarrow& \displaystyle \frac{\sigma^{2}}{n}( 1 - 0) \\
&=& \displaystyle \frac{\sigma^{2}}{n} \\
\end{eqnarray}
これは、独立と仮定した場合の結果と同じになります。
まとめ
上では復元と非復元、そして無限母集団と有限母集団でまとめると以下のようになりますね。
| 母集団が有限 | 母集団が無限 | |
|---|---|---|
| 復元 | 超幾何分布 | 復元・有限に対して\(n→∞\) |
| 非復元 | \(\frac{1}{n}*\frac{1}{n-1}*...\) | 非復元・有限に対して\(n→∞\) |