
https://docs.google.com/spreadsheets/d/1pynuU2-fxmpPzQOm-fRA1dyOt68k3226OdrVb7WSVW0/edit#gid=389175346
Contents
分割表の検定の検定統計量
ここで扱う検定統計量はとにかく以下ピアソンのカイ二乗のみです。
これだけ覚えれば問題ないです。
自由度を\(a\)とした時、
\begin{eqnarray}
\chi^{2} = \sum_{i=1}^{n} \frac{(X-E[X])^{2}}{E[X]}
\end{eqnarray}
は、自由度\(a-1\)の\(\chi^{2}\)分布に従う。
\(X\):観測度数(実際に観測された数値)
\(E[X]\):期待度数(理論的に、観測値はわからないけど、全ての件数がわかっている状態で導き出した期待値)
自由度:n-1
\(X-E[X]\)を\(|X-E[X]|-0.5\)に置き換えたものをイェーツの補正と言います。
通常分割表検定は離散データを扱うわけですが、離散の場合、通常ヒストグラムを書くと確率密度関数は真ん中の0.5、1.5、2.5、、、を通っていきます。
しかし確率変数0は0以上1未満の値を示すわけです。となると
自由度を\(a\)とした時、
\begin{eqnarray}
\chi^{2} = \sum_{i=1}^{n} \frac{(|X-E[X]|-0.5)^{2}}{E[X]}
\end{eqnarray}
は、自由度\(a-1\)の\(\chi^{2}\)分布に従う。
分割表検定(適合度検定)
1×a分割表(確率変数がaコ)で、このデータがどの分布に適合しているのかを検定するものになります。
期待度数:これに適合するだろうと仮定した分布の確率変数の期待値から出した各確率変数の予測件数
ポアソン分布などの結果が疑わしい時に、
本当にこの件数がポアソン分布なのかどうかを検証するためのものが適合度検定と呼びます。
適合度検定(分割表)
期待度数:確率の計算からこのくらいのデータ件数になるだろうという予測値
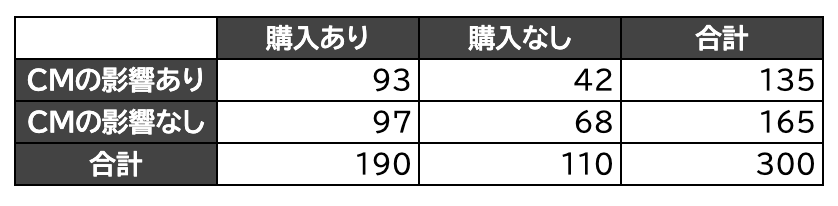
「CMの影響あり」で「購入あり」の観測度数はそのまま上で93です。
期待度数を考える
そしてこの「CMの影響あり」で「購入あり」の期待度数を考えます。
300人アンケートに答えて、
CMの影響ありと答えた人は135人です。この比率(確率)は\(\displaystyle \frac{135}{300}\)です。
ということは、その状況で購入ありと答えた人は全体で190人いるので、そのうち\(\displaystyle \frac{135}{300}\)がCMの影響ありと答えるだろうと予測されます。
そのため、
「CMの影響あり」で「購入あり」の期待度数は\(190 \cdot \displaystyle \frac{135}{300}\)となります。
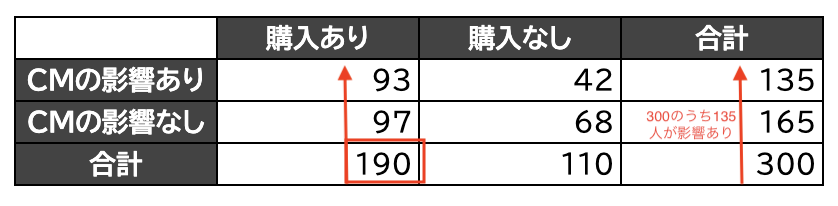
もちろん逆に捉えて計算をしても、
結果「CMの影響あり」で「購入あり」の期待度数は\(135 \cdot \displaystyle \frac{190}{300}\)となります。
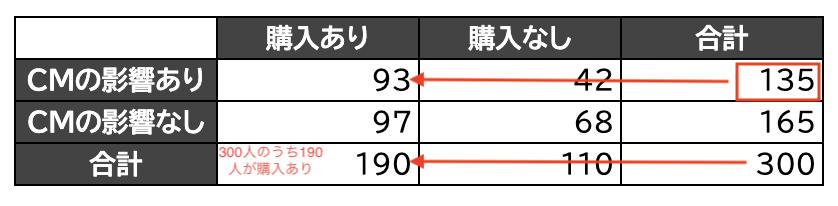
これにより、
それぞれのセルの観測度数と期待度数は、
「CMの影響あり」で「購入あり」の観測度数は93、期待度数は\(190 \cdot \displaystyle \frac{135}{300} = 85.5\)
「CMの影響あり」で「購入なし」の観測度数は42、期待度数は\(110 \cdot \displaystyle \frac{135}{300} = 49.5\)
「CMの影響なし」で「購入あり」の観測度数は97、期待度数は\(190 \cdot \displaystyle \frac{165}{300} = 104.5\)
「CMの影響なし」で「購入なし」の観測度数は68、期待度数は\(110 \cdot \displaystyle \frac{165}{300} = 60.5\)
となるので、まず
分割表での検定統計量は、
\begin{eqnarray}
\chi^{2} = \frac{(93-85.5)^{2}}{85.5} + \frac{(42-49.5)^{2}}{49.5} + \frac{(97-104.5)^{2}}{104.5} + \frac{(68-60.5)^{2}}{60.5}
\end{eqnarray}
となります。
自由度
各行、列、表の合計値がわかっているとする。
この時例えば「CMの影響あり」で「購入あり」は実際の件数が93がわかったとする。
そうすると他の3つのセルは確定する。
そのため自由に値が取れるものは1つであり、それ以外は合計から引き算することで決まります。
なので自由度は1となります。
これは2*2分割表なので、\((2-1)*(2-1)=1\)となります。\(n\)*\(n\)分割表なら自由度は\((n-1)*(n-1)\)となります。
独立性の検定
独立性を検証するためには、
\(p_{ij} = p_{i} \cdot p_{j}\)が成立することです。
実は上の分割表の適合度検定と、この独立性検定、同じ検定になります。
「CMの影響あり」となる割合(確率)は、\(\displaystyle \frac{135}{300}\)
「購入あり」となる割合(確率)は\(\displaystyle \frac{190}{300}\)
これらが同時に成り立つ、つまり「CMの影響あり」で「購入あり」となる確率は独立と仮定するのであれば、それぞれを掛けた\(300 \cdot \displaystyle \frac{190}{300} \cdot \frac{135}{300} \)
確率でも同時に成り立つ場合は、積の確率となります。
\(300 \cdot \displaystyle \frac{190}{300} \cdot \frac{135}{300} = 190 \cdot \frac{135}{300} \)となり、これは、上の適合度検定での「CMの影響あり」で「購入あり」の期待度数と一緒になります。
よく見ますが、f(x,y) = g(x)h(y)は独立です。互いにxとyの式が影響与えない。
一様性の検定
一様性ということなので、こちらも観測度数と期待度数の差を考えます!なので検定統計量はカイ二乗検定になります。
原理は
普通に得られた観測度数の数値。
そして一様性があると仮定した上(帰無仮説)の場合、すべての確率変数の出る確率は等分になる。なので観測度数の合計が100だとした時、確率変数が10個あれば、それぞれが等分で出るので、それぞれの確率変数は10個ずつ観測するはずである。
期待度数:一様性がある(各確率変数の出る確率が同じ)と仮定した上での各確率変数の予測件数
例)
サイコロを36回投げた時に、
実際の観測が以下のようになったとします。
この時、サイコロは一様性があり確率は1/6である。そのため、普通なら36回投げてそれぞれ6回ずつ出るはずです。

しかし、そんなことはなくずれが生じています。
このずれに対して検定をします。

よってピアソンのカイ二乗検定を用いて、
\begin{eqnarray}
\chi^{2}
&=& (5-6)^{2} + (4-6)^{2} + (8-6)^{2} + (5-6)^{2} + (6-6)^{2} + (8-6)^{2} \\
&=& 14
\end{eqnarray}
カイ二乗分布\(\chi^{2}\)の有意水準表
自由度が2の場合のカイ二乗分布の有意水準\(alpha\)を5%(0.05)とした時、5.99となります。
F分布\(F\)の有意水準表
カイ二乗分布の有意水準表とは表形式が違うため、少々戸惑う部分があるかと思います。
有意水準ごとに分布表があります。
カイ二乗分布や標準正規分布表などの場合は、1つの表のみでしたが、このF分布では優位水準ごとに分布表があります。
その理由としては、カイ二乗分布や標準正規分布表は自由度が1種類しかないが、
F分布の場合、分子と分母で2つの自由度があります。
読み方としては、分子の自由度を\(v_{1}\)、分母の自由度を\(v_{2}\)とした時、
.jpg)