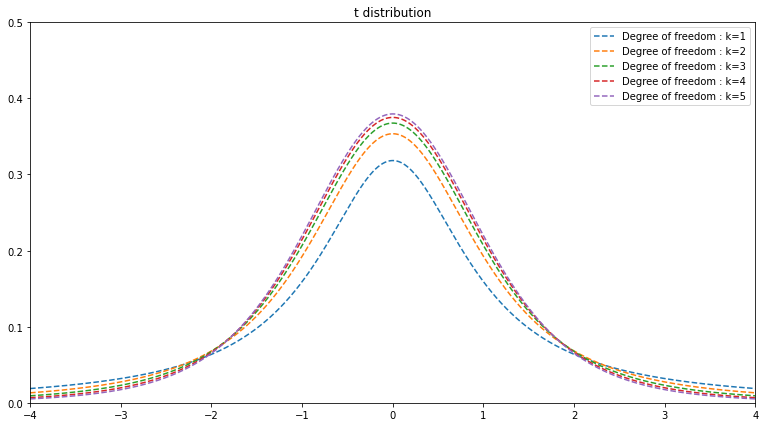
みなさん、t分布と聞いて何を思い出しますか?
統計をやってる方であれば、
なんだか正規分布に近しい形とか、よく信頼区間を出すときに出てきたりするーとか色々思い出すことがあるかと思います。
t分布は、
正規分布する母集団の平均と分散が未知で標本サイズが小さい場合に平均を推定する問題に利用される。
つまり、正規分布に近しい形で平均はわかってるけど、母分散がわからない時に使用する分布のことです。
どうにか母分散を求めて、正規分布にして扱っても良いかもだけど、母分散がわからない時にはこっちの分布を使うとより正確だよーということです。
平均がわかっているけど、母分散がわからない。
実際これはそれなりにデータが得られてる標本データがあり、そこから標本分散は求めれる。
でも母分散となると推定が難しい。正確に母分散を求めることはできなそう。
なので、ここで思いつくのが、不偏分散!
標本データから不偏分散を用いることで、母分散の推定ができるというわけです!
すなわち、正規分布に平均は母平均、分散は不偏分散を入れてあげて計算すれば良い!ということが言えそうですね!
t分布というとどうしても難しく捉えてしまいがちですが、実は定義をしっかり確認した上で、落としていけば結構当たり前のことをやってると想像できたでしょう!
そして導出自体も難しくありません。
確率変数を\(X\)、平均を\(E[X]\)、不偏分散を\(U\)とした時、
t分布での確率変数\(T\)は、
\( T= \displaystyle \frac{X-E[X]}{\sqrt{U}} \)
と表せます。
そして、不偏分散\(U\)は\(U = \frac{1}{n-1} \sum_{i=1}^{n} (X_{i}-E[X])^{2} \)となることから、
\( T= \displaystyle \frac{X-E[X]}{\sqrt{ \displaystyle \frac{1}{n-1} \sum_{i=1}^{n} (X_{i}-E[X])^{2} }} \)となります。
↓
t検定は確か、母平均がわかってて、母分散がわかっていない状態で使用する検定だよね!
↓
その状態で有意水準を考えるということは、t分布は母平均がわかってて、母分散が不明の分布ってことだよね!
↓
でも母分散は不明の場合、どう推定しようかな、、、あ!不偏分散で代用すれば標本データから母集団の分散の推定ができる!
↓
母平均はわかってて、母分散は不偏分散で求めれば、t分布は導出できそう!
って覚えれば、余裕ですね!
\(t\)分布の導出
改めて、t分布の定義を確認すると、
\(t\)分布では\(Z~N(0,1)\)と\(\chi^{2}\)分布は互いに独立なので、
\(f(Z,\chi^{2}) = f(Z)\cdot f(\chi^{2})\)
と表せる。
そして、実際に\(f(Z,\chi^{2})\)がもとまり、
ここで、これは\(Z\)と\(\chi^{2}\)の式となるので、
\(T=\frac{Z}{\sqrt{\frac{U}{n}}} \)を代入すれば、
\(f(T,U)\)の式になります。
しかしこれではまだ\(U\)が残っているので、厳密に確率変数\(T\)の確率密度関数ではありません。
なので、\(U\)で積分すれば\(U\)が消えて、\(f(T)\)の確率密度関数になる。
\(t\)分布の導出
まず確率変数\(X\)は標準正規分布\(X \sim N(0,1)\)に従い、確率変数\(Y\)は\(\chi^{2}\)分布に従うと仮定から、
\begin{eqnarray}
f(x) &=& \frac{1}{\sqrt{2\pi}}{\exp \biggr\{ -\frac{x^{2}}{2} \biggr\}} \\
g(y) &=& \frac{y^{\frac{n}{2}-1} \exp(-\frac{y}{2})}{ 2^{\frac{n}{2}}\Gamma(\frac{n}{2})}
\end{eqnarray}
と書け、この2つは互いに独立なので、以下のように表せます。
\begin{eqnarray}
h(x, y) &=& f(x)g(y)
\end{eqnarray}
したがって、
\begin{eqnarray}
h(x, y)
&=& f(x)g(y) \\
&=& \frac{1}{\sqrt{2\pi}} {\exp\biggr\{-\frac{x^{2}}{2}\biggr\}} \cdot \frac{y^{\frac{n}{2}-1} \exp(-\frac{y}{2})}{ 2^{\frac{n}{2}}\Gamma(\frac{n}{2})}
\end{eqnarray}
現在上記関数が、\(x\)\(と\)yの2変数の関数になっているので、\(t\)分布を求めるには\(t\)に変換をさせないといけません。
そのため、\(T=\frac{Z}{\sqrt{\frac{U}{n}}} \)を用いて変換します。
いきなり、\(x\)と\(y\)の両方を同時に\(t\)で表現することはできないので、まず\(x\)を\(t\)に置き換えてみます。
\(t=\frac{x}{\sqrt{\frac{y}{n}}} \)より、
\begin{eqnarray}
t &=& \frac{x}{\sqrt{\frac{y}{n}}} \\
x &=& t\sqrt{\frac{y}{n}}
\end{eqnarray}
(yでも良いけど、ルートがついていて面倒なので今回はxを置換)
したがって、
\begin{eqnarray}
f \left(t\sqrt{\frac{Y}{n}}, y \right)
&=& \frac{1}{\sqrt{2\pi}}{\exp\biggr\{-\frac{(\sqrt{\frac{y}{n}})^{2}}{2}\biggr\}} \cdot \frac{y^{\frac{n}{2}-1} \exp(-\frac{y}{2})}{ 2^{\frac{n}{2}}\Gamma(\frac{n}{2})} \\
&=& \frac{1}{\sqrt{2\pi}}{\exp\biggr\{-\frac{(\sqrt{\frac{y}{n}})^{2}}{2}\biggr\}} \cdot \frac{y^{\frac{n}{2}-1} \exp(-\frac{y}{2})}{ 2^{\frac{n}{2}}\Gamma(\frac{n}{2})}
\end{eqnarray}
最終的にはt分布なので、tの式だけにする必要があります。
なので、xが消えた今、yについて積分をすることによって、tの式だけになり、t分布になると想像できるかと思います。
なので、両辺を積分してみましょう!
\begin{eqnarray}
\Gamma(n)
&=& \int_{0}^{\infty} x^{n-1}e^{-n} dx
\end{eqnarray}
※ ただしn > 0として、nは自由度。
from scipy.stats import t
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
fig = plt.figure(figsize=(13,7))
x = np.linspace(-4, 4, 10000)
# 自由度
k_degree = [1, 2, 3, 4, 5]
for i in k_degree:
plt.plot(x, t.pdf(x, i), linestyle='--', label='Degree of freedom : k={}'.format(i))
plt.title("t distribution")
plt.xlim(-4, 4) # X軸
plt.ylim(0, 0.5) # Y軸
plt.legend() # 凡例
plt.show()