
Contents
ベイズの定理の導出
まず条件付き確率の定義から、
\begin{eqnarray}
p(\theta|x) &=& \frac{p(x, \theta)}{p(x)} ・・・①\\
p(x|\theta) &=& \frac{p(x, \theta)}{p(\theta)} ・・・②
\end{eqnarray}
が成立するので、事後分布の式となる\(p(パラメータ|確率変数)\)、つまり\(p(\theta|x)\)の式を変形していくと、
\begin{eqnarray}
p(x, \theta) &=& p(x|\theta)p(\theta) ・・・②'
\end{eqnarray}
\(①\)に\(②'\)を代入すると、
\begin{eqnarray}
p(\theta|x)
&=& \frac{p(x, \theta)}{p(x)} \\
&=& \frac{p(x|\theta)p(\theta)}{p(x)} \\
&=& \frac{p(x|\theta)p(\theta)}{\displaystyle \int p(x|\theta)p(\theta)d\theta}
\end{eqnarray}
となります。
よく上のような式の使われ方をします。
いきなり\(p(x)\)が積分になりましたが、実際に\(\theta\)で積分をすると\(p(x)\)のみになります。
このように分子の式に対して分母は積分すると数値に表現することができるため、最終的には以下のような式として表現されることが多いです。
以下の式をベイズの更新式になります。
\begin{eqnarray}
p(\theta|x) &\propto& p(x|\theta)p(\theta) \\
事後分布 &\propto& 尤度関数 \cdot 事前分布
\end{eqnarray}
階層ベイズモデル
ベイスの更新式は上では実際にパラメータとデータは1つずつのように記載していますが、複雑なモデルになるとパラメータが2つになったりします。
よくある例としては、正規分布。
正規分布では、パラメータは平均と分散の2つがあります。このパラメータによって正規分布の形も変わればそこから得れるデータも変わります。
なので正規分布のパラメータを更新していくベイズモデルは、正規分布の確率分布をpとした時、
パラメータの箇所を\(\mu, \sigma^{2}\)に置き換えて、
\begin{eqnarray}
p(\mu, \sigma^{2}|x) &\propto& p(x|\mu, \sigma^{2})p(\mu, \sigma^{2}) \\
\end{eqnarray}
と表現できます。
でもそもそも分散の値は平均を基準としたデータとの距離の2乗の和なので、分散は平均に依存するというのがなーんとなく伺えると思います。
ということは、分散は実際平均\(\mu\)の式で表せます。(分散の定義からも期待値が入ってる)
なので、パラメータの依存関係として、\(\mu → \sigma^{2}\)というようになるので、以下のようにも考えれそうです!
分散\(\sigma^{2}\)は、\(\mu\)の条件つきということで、
\begin{eqnarray}
p(\sigma^{2}|\mu)
&=& p(\sigma^{2},\mu)p(\mu) \\
p(\sigma^{2},\mu) &=& p(\sigma^{2}|\mu)p(\mu)
\end{eqnarray}
従って、
\begin{eqnarray}
p(\mu, \sigma^{2}|x) &\propto& p(x|\mu, \sigma^{2})p(\sigma^{2}|\mu)p(\mu) \\
事後分布 &\propto& 尤度関数 \cdot \sigma^{2} の事前分布 \cdot \mu の事前分布
\end{eqnarray}
と表せることができました。
このようによりパラメータの依存関係も考えていき、事前分布を階層考えたものを、階層ベイズモデルと言います。
もちろん上記の依存関係を考えたりせず、ベイズ更新を行うことはできますし、より精緻に更新をしたい場合は、上記のような依存関係をも考えた上でのベイズ更新式を立てる必要があります。
ベイズの更新の原理
そもそもベイズ更新は何の目的で行うものなのか?
それは、データxから確率分布を仮定した上で、真のパラメータを推定するためのものです。
そして上ではベイズの更新式やベイズの階層モデルを考えていきましたが、実際にここではでは更新式といえど、どのようにして更新していくのか?そもそも何を更新していくのか?について説明していこうと思います!
再度、ベイズ更新式を再掲します。
\begin{eqnarray}
p(\theta|x) &\propto& p(x|\theta)p(\theta) \\
事後分布 &\propto& 尤度関数 \cdot 事前分布
\end{eqnarray}
1つずつ式を見ていきますが、
まず事後分布。事後分布の式を見ると、xというデータを条件にしたパラメータの条件付き確率になっています。
そして尤度関数。尤度関数は言わずもがなですが、尤度関数というとイメージ、パラメータの最尤推定量を求めるというイメージなると思いますが、ここではただの確率分布だと思ってください。(なぜか本では尤度関数という記載がある)
最後、事前分布。こちらはパラメータの確率分布になります。純粋にそのパラメータの出る確率を意味します。
なので更新していくと、どんどん新しいパラメータが上書きされていきます。
そして収束していき、真のパラメータの推定ができるということになります。
xを尤度関数でサンプリングしていくとありますが、関数からではなく、実際にリアルタイムに採れたデータをそのまま取り込んでいくのでOKです。
そして原理を説明していくと、
ここで尤度関数からデータを取るためには、サンプリングという処理が必要になります。
このサンプリングは簡単な関数である正規分布などであれば、事後分布で得られたパラメータ(サンプリング)を正規分布に入れて、
そこから新たなデータxをサンプリングします。
そして事後分布ではxを条件にしているので、尤度関数で得られたxを使って、新しい事後分布を構築しそこから新しいパラメータをサンプリングします。
そうすると、また今度尤度関数に新しいパラメータを入れて、新しいxを出して、そのxを用いて事後分布構成して、新しいパラメータをサンプリングして、またそのパラメータを尤度関数に入れて、、、、、
を繰り返していきます。
実際は更新としては、事前分布は更新作業にはそこまで影響はせず、
尤度関数と事後分布で更新はできてしまいます。
で、事後分布で最適なパラメータを出すためには、
MAP推定量(maximum a posteriori, MAP)という最大事後確率です。
これを求めるには、最終的な真のパラメータとの差異を見る
予測分布
もちろん真のパラメータが推定できたとする。この時の事後分布を用いて、最終的には次に出るデータを予測したいですよね!
その予測をするための式を定義します。
今実際の本データで\(x_{n}\)が出たときに、
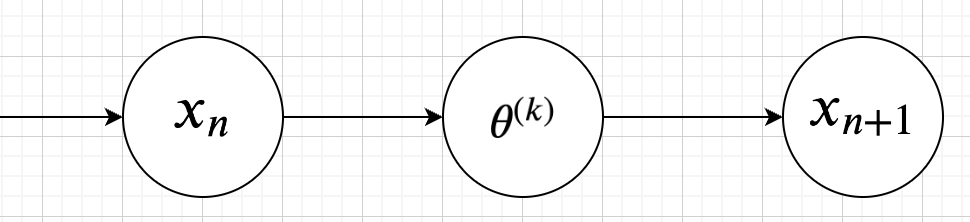
以下のように定義します。
\begin{eqnarray}
p(x_{n+1}|x_{n}) &=& \int p(x_{n+1}|\theta)p(\theta|x_{n}) d\theta\\
予測分布 &=& \int
\end{eqnarray}
データ\(x_{n}\)から、次のデータ\(x_{n+1}\)を予測するので、予測分布はデータ\(x_{n}\)を条件にした条件付き確率で表現されます。
上記式から、すべてのどんなパラメータも積分して完全にパラメータを消し去ろうとしています。
事後分布で構築したパラメータの分布のパラメータすべてで積分します。
予測分布に使う事後分布ではほとんど精緻なものなわけで、
マルコフ連鎖もいろんなデータから次の状態への遷移をすべてのパターンで確率の和で求めています。
要は以下のような仕組みです。
和は離散、インテグラルは連続です。
\begin{eqnarray}
p(x_{n+1}|x_{n})
&=& p(x_{n+1}|\theta_{1})p(\theta_{1}|x_{n}) + p(x_{n+1}|\theta_{2})p(\theta_{2}|x_{n}) + ・・・ + p(x_{n+1}|\theta_{k})p(\theta_{k}|x_{n}) \\
&=& \int p(x_{n+1}|\theta)p(\theta|x_{n}) d\theta
\end{eqnarray}
パラメータがx_{n}とx_{n+1}の間に入っている状態です。というか隠れマルコフモデルか。
自然共役分布・共役事後分布と共役事前分布
事後分布と事前分布はパラメータに関する分布になりますが、
その2つの分布が同じ分布になる場合、共役という。
ベイズの更新(尤度なし)
# 必要なライブラリの追加
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
# 標準化処理
def normalise(y,x):
return y / np.trapz(y, x)
# ベルヌーイの試行結果
results = np.array([1,0,1,0,1,0,1,1,1,1,1,0,1,1,1,0,1,1,1,1])
N = 201
# Values of theta on [0, 1]
theta = np.linspace(0 ,1 , N)
# 事後分布の初期値(y=1.0)
prior = normalise(np.repeat(1, N), theta)
# ベルヌーイは1が成功、0が失敗とする。ベルヌーイ分布の更新処理
from matplotlib.projections import process_projection_requirements
def bernoulli_model(k, theta, prior):
posterior = theta**k * (1 - theta)**(1 - k) * prior
return normalise(posterior, theta)
# ベイズの更新処理
fig, ax = plt.subplots(ncols =5, nrows = 4, figsize=(16,16))
ax = np.ravel(ax)
for n in range(20):
ax[n].plot(theta, prior, linestyle="--") # 事前分布
posterior = bernoulli_model(results[n], theta, prior) # 事後分布の更新
ax[n].plot(theta, posterior) # 事後分布
ax[n].set_title("Bernoulli Trial Results: %d" % results[n], loc="left")
prior = posterior # 事前分布に前の更新された事後分布を適用
plt.show()
実際に実行してみると、以下のように
青色の点線が事前分布で、オレンジの実線が事後分布を示し、徐々に収束していくのが見て取れます。
横軸はベルヌーイ分布の成功の確率で、盛り上がりを見せているのは0.75付近となります。
今回ベルヌーイ分布の成功は1で表していますが、20回の試行のうち15回が試行成功なので、パラメータとなる成功確率は0.75と標本データからはわかります。
そのため、ベイズの更新がうまくできていそうです。
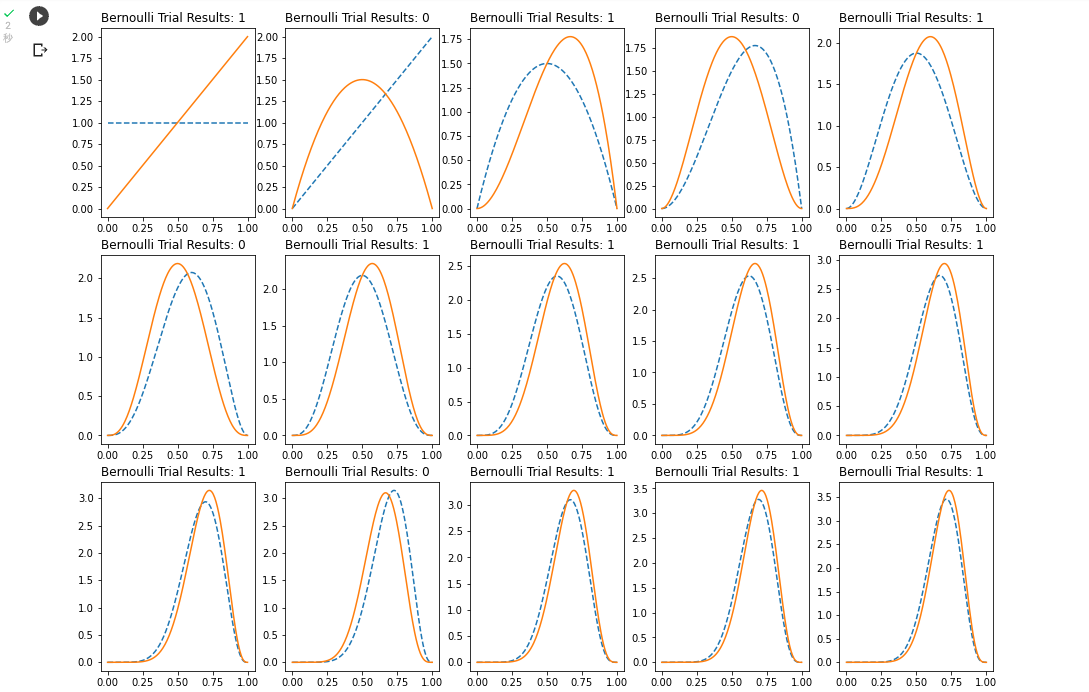
今回ここでは事前分布に事後分布を直接入れているので、事前も事後もともにベルヌーイ分布で更新をかけています。
ベイズの更新の式では、尤度が入ってますが、尤度は基本的にはサンプリングです。
要は、事前分布のパラメータ情報を条件にして尤度を構成してそこからデータをサンプリングして、それを事後分布に食わせて更新をかけます。
今回はすでにresultという結果のデータがあるのでそちらを用いているので、そのデータを用いているのでサンプリングなどは行っていないということになります。
ベイズの更新(尤度あり)
二項分布は事後分布にベータ分布、事前分布にベータ分布で共役分布を持ちます。
そのため、以下のように
\begin{eqnarray}
事後分布 &\propto& 尤度関数 \cdot 事前分布
\end{eqnarray}
と考えることができるので、
実際にプログラムを書いてみると以下のようになります。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
def normalise(y,x):
return y / np.trapz(y, x)
def binomial_model(k, n, alpha, beta):
theta = np.linspace(0,1,201)
# 事前分布と事後分布を
prior = stats.beta(alpha, beta)
posterior = stats.beta(alpha + k, beta + n - k)
# 各thetaの値に対して尤度値を算出。
likelihood = [stats.binom.pmf(k, n, p) for p in theta] # k:成功回数、n:試行回数、p:1回試行したときに成功となる確率
likelihood = normalise(likelihood, theta) # 尤度値を標準化(尤度関数)
plt.figure(figsize=(16,4))
plt.plot(theta, prior.pdf(theta), label="Prior", linestyle="--")
plt.plot(theta, posterior.pdf(theta), label="Posterior")
plt.plot(theta, likelihood, label="Likelihood (normalised)")
plt.xlim((0,1))
plt.legend();
return (theta, posterior)
binomial_model(7,10,2,2)
あくまで主役は確率変数の分布を考えている二項分布で、この二項分布がどんどん形を更新していきます。
その形の更新のためにベータ分布が使われているというだけです。
theta = np.linspace(0,1,201)
で、二項分布のパラメータである成功確率を0から1の値を201等分にして、
0.005、0.01、、、とそれぞれ固定した上でどのくらい尤度の値が高いかをそれぞれ算出していきます。
例えば、theta = 0.005とした上で、試行回数がnの時成功した回数がkの場合はどのくらいあり得るのか?を尤度でそれぞれ出しています。
stats.binom.pmf(pmf:probability mass function 確率質量関数)は二項分布で、k:成功回数、n:試行回数、p:1回試行したときに成功となる確率(ベルヌーイの成功確率)です。
つまりtで小さく確率を定義しておいて、それで一番尤度が高いところのpがいわゆる最尤法の最尤推定量になります。
この時のpを用いて、事後分布で最適化を行います。
ベイズの更新の具体例
自然共役事前分布と仮定する。
確率分布をポアソン分布と仮定すると、事後分布と事前分布はガンマ分布になることを利用します。
\(\pi(\lambda|x) \propto f(x|\lambda) \pi(\lambda) \)
事後分布 \(\propto\) 尤度 \(\cdot\) 事前分布
\(\pi\):ガンマ分布
\(f(X)\):ポアソン分布
ガンマ分布はパラメータとして\(\alpha\)、\(\beta\)を用いて、
事前分布は\(\pi(\lambda|\alpha, \beta)\)
事後分布は\(\pi(\alpha, \beta|x)\)
ポアソン分布はパラメータとして\(\lambda\)を用いて、
尤度は\(f(x|\lambda)\)
とします。
この時、ベイズの定理より、
\begin{eqnarray}
\pi(\lambda|\alpha, \beta)
&\propto& f(x|\lambda) \pi(\lambda|\alpha, \beta)
\end{eqnarray}
となり、計算をすると以下の2つの式が導出されます。
これがベイズの更新式となります。
\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha_{1} &=& \alpha_{0} + x \\
\beta_{1} &=& \beta_{0} + 1
\end{array}
\right.
\end{eqnarray}
\(\alpha_{0}\)と\(\beta_{0}\)は最初の事前分布からサンプリングしたパラメータ(別になんでも良い。)で、
\(x\)はポアソン分布からサンプリングされたデータを表している。もちろんサンプリングではなく、普通にとれた\(x\)をイメージすると良い。
これらは、ベイズの定理の右辺である、尤度と事前分布から取れたデータとなっています。
この2つのデータを上記のベイズの更新式に入れることで、左辺の\(\alpha_{1}\)、\(\beta_{1}\)が求まります。
この\(\alpha_{1}\)、\(\beta_{1}\)は事後分布の確率変数になります。
そして\(\alpha_{1}\)、\(\beta_{1}\)が求まったので、今度はこの2つの値を右辺の\(\alpha_{0}\)、\(\beta_{0}\)に代入して、また\(x\)をサンプリングして、事後分布の確率変数を更新します。
以下のようなイメージです。
\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha_{2} &=& \alpha_{1} + x \\
\beta_{2} &=& \beta_{1} + 1
\end{array}
\right.
\end{eqnarray}
今回のベイズ更新式は簡単なので、以下のように漸化式とした時、
\(n\)番目の値で、\(n+1\)番目の値を更新していき、
\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha_{n+1} &=& \alpha_{n} + x \\
\beta_{n+1} &=& \beta_{n} + 1
\end{array}
\right.
\end{eqnarray}
を繰り返し計算すると、
\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha_{n+1} &=& \alpha_{1} + \displaystyle \sum_{k=1}^{n} x_{k} \\
\beta_{n+1} &=& \beta_{1} + n
\end{array}
\right.
\end{eqnarray}
となり、複数の\(x\)のデータが得られれば、for文などを用いて繰り返し処理しなくても、通常\(n\)回更新をして得られるパラメータが、一括で求めることができます。
# ベイズ更新
import math
import numpy as np
import scipy.special
from scipy import stats
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
from scipy.stats import gamma, norm, poisson
import scipy.special as sp
%matplotlib nbagg
fig = plt.figure(figsize=(7,7))
# 初期パラメータ
alpha = 3
beta = 1
lambda_ = 3
# 確率変数
y = np.arange(1,10, 0.1)
# 事前分布、事後分布であるガンマ分布の定義
def gamma_prob(x):
global alpha, beta
C = beta**alpha / sp.gamma(alpha)
dens = C * x**(alpha - 1.0) * np.exp(-beta * x)
return dens
# 尤度であるポアソン分布の定義
def poiason_prob(x):
global lambda_
result = (lambda_**x) * (np.exp(-lambda_)) / scipy.special.factorial(x)
return result
# ベイズ更新
def bayes_update(i):
global alpha, beta, y, lambda_
plt.cla()
# 尤度のポアソン分布から1つ確率変数サンプリング
x = np.random.poisson(lam=lambda_, size=1)
x = x[0]
#plt.plot("事前分布:alpha={}, beta={}".format(alpha, beta))
plt.plot(y, gamma_prob(y), color="red") # 事前分布
# ベイズ更新式
alpha = alpha + x
beta = beta + 1
plt.plot(y, poiason_prob(y), color="green") # 尤度
plt.plot(y, gamma_prob(y), color="blue") # 事後分布
animation_obje = animation.FuncAnimation(fig, bayes_update, frames = np.arange(1,30), interval=120)
rc('animation', html='jshtml')
animation_obje