ここでは回帰診断図という、回帰分析に使用したデータがどのくらい分析結果に影響を与えているかを確認することのできるものがあります。
回帰分析を行うとき、外れ値のデータを取り込んで実行してしまったとき、回帰曲線/回帰直線がかなり外れデータのある方に引っ張られてしまいます。
回帰分析は最小二乗法を用いて分析します。
最小二乗法とは求める回帰直線などを仮定した上で、その直線と各データとの距離の2乗の和の最小値を求めます。
そのため、外れ値はその直線との距離が大きく、その分外れ値の方に回帰直線が引っ張られてしまうので、分析結果に悪影響を与えてしまいます。
なのでそのような外れ値はどれかなどを確認するために、回帰診断図を見て、このデータを外して分析するなどを考察することができます。
ここではそんな回帰診断図についてまとめて行こうと思います。
回帰診断図とは
回帰診断図とは、Rなどで回帰分析をした結果として、実際の取れたデータが回帰分析の結果にどのくらい影響を与えているのかなどを実際にグラフィカルに可視化・分析してくれるものになります。
この診断図を見ることで、外れ値を確認して除いたり、などを見ることができます。
主に以下のようなプロットが回帰診断図になります。

項目としては、
- 1.Residuals vs Fitted
- 2.Normal Q-Q
- 3.Scale - Location
- 4.Residuals vs Leverage
となります。
それぞれ1つずつどういった内容なのかと分析について話していこうと思います。
まず大前提として、プロットされた各点は回帰分析に使用した各データを示します。
特に影響力の強いデータは図中にラベルが与えられます。
回帰分析を実行する際の仮定
誤差については以下のような仮定が存在します。
誤差の期待値が0
\(E[\epsilon] = 0\)
誤差の分散が均一である(等分散性)
\(V[\epsilon] = \sigma^{2}\)
誤差が正規分布に従う
上で期待値が0、分散が\(\sigma^{2}\)なので、
\(\epsilon \sim N(0, \sigma^{2}) \)
誤差が独立である(または無相関である)
\(E[\epsilon_{i}\epsilon_{j}] = 0\)
( \(cov(\epsilon_{i}, \epsilon_{j}) = 0\) )
無相関でないなど、系列相関と呼ばれ、ダービンワトソンなどで検定を行う。
完全な多重共線性がない
※ これは誤差関係ないが、、分散拡大係数 (VIF) による診断
回帰診断法は、この上記の仮定がそもそも成り立っているのかどうかを見て、外れ値がないかなどを判定するものとなります。
そのため、上記の仮定が成り立たないとそもそも回帰分析の最小、、、、値が取れないということにもなります。
残差の性質
そして実際回帰診断図を読んでいくにあたり、回帰診断図の中身は"誤差"ではなく"残差"を扱うことになるので、残差の定義や性質についてもここで振り返っておきます。
まず残差の定義としては、
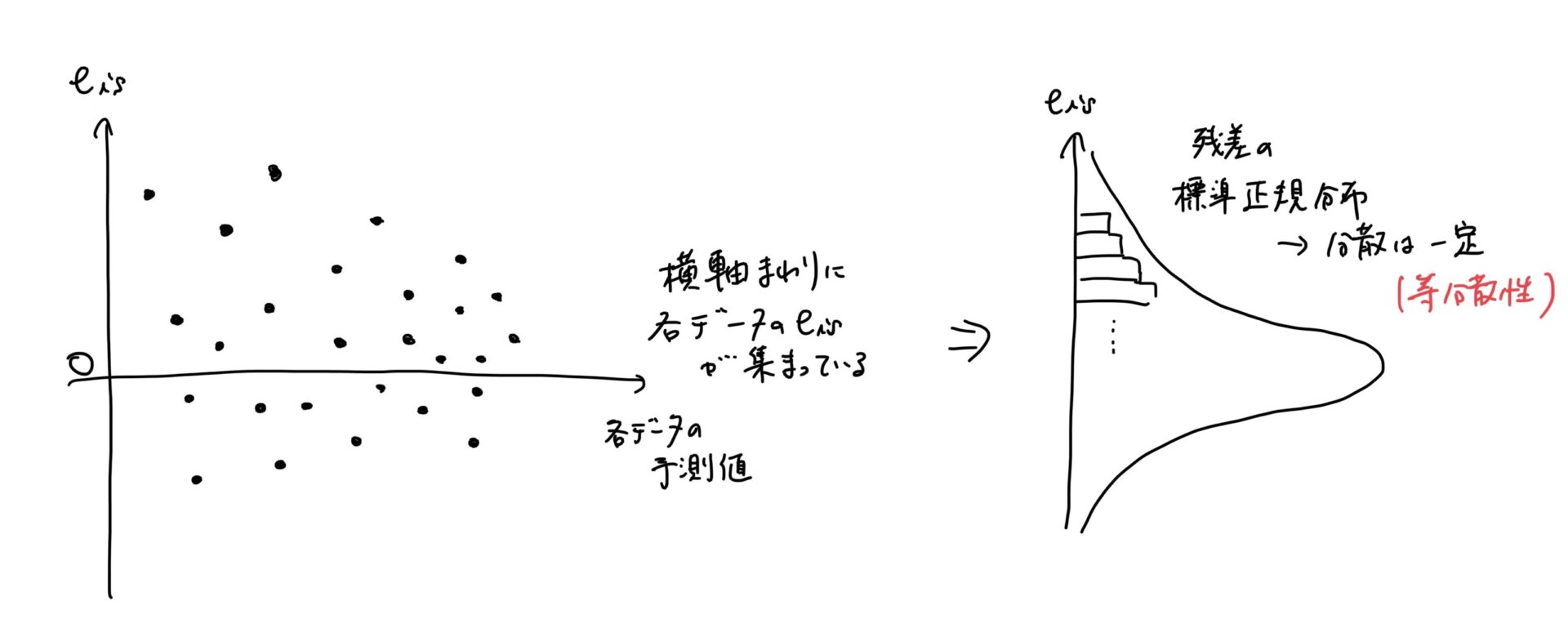
そして残差の性質に行く前に、残差の分布について考えてみたいと思います。
まずあるデータの残差、予測値、実測値について、
\begin{eqnarray}
e_{i} = y_{i} - \hat{y_{y_{}}} = (a - \hat{a_{}})x_{i} + \epsilon_{i}
\end{eqnarray}
となり、\(n\)が大きくなると、\(a\)の最小二乗推定量である\(\hat{a_{}}\)は確率収束するので、\((a - \hat{a_{}})\)はほぼ0に収束していきます。
そのため、上記式は\(n\)が大きくなると、誤差で仮定した分布\( e_{i} \sim N(0, \sigma^{2}) \)と残差\(\epsilon_{i}\)はほぼ同じ分布になります。
そのため、誤差で仮定した内容が基本的には残差でも同じような性質として扱うことができます。
残差の期待値が0
\(E[e] = 0\)
残差プロットによる診断(本ページの1.Residuals vs Fitted)
残差の分散が均一である(等分散性)
\(V[e] = \sigma^{2}\)
残差プロットによる診断(本ページの1.Residuals vs Fitted, 3.Scale - Location)
残差が正規分布に従う
上で期待値が0、分散が\(\sigma^{2}\)なので、
\(e \sim N(0, \sigma^{2}) \)
正規QQプロットによる診断(本ページの2.Normal Q-Q)
誤差が独立である
\(E[e_{i}e_{j}] = 0\)
この性質を実際に回帰診断図で見て考察をしていこうと思います。
回帰診断図
1.Residuals vs Fitted
横軸がFitted Valueで予測値、縦軸がResidualsで残差です。
残差は予測値\( \hat{y_{}} \)と実測値\( y \)で表されます。
ここでは以下のようなことを確認します。
- 外れ値があるか
- 残差の性質の等分散性を満たしているか
外れ値の場合は、この残差がかなり大きくなります。
残差はnが大きくなると分散が一定なので、それがあってるかどうかを検証します。
分散が一定であれば、基本的にランダムに残差の期待値である0よりプラスか、マイナスかになります。
通常回帰分析はこの等分散性を仮定しているので、これが成立した上で回帰分析ができます。
これができない場合は、分析ができません。
例えば、最小二乗法使う時、誤差の2乗を計算します。
その誤差に相関があるかをみるのが、ダービンワトソンになります。
そのため残差プロットした時に、外れ値を見つけやすい!
さらには等分散性があり、期待値は0なので普通であればその周りにランダムに散らばる。
しかし傾向を持ったりする物もある。プラスが続いたり、マイナスが続いたり
それは、残差が独立でないという性質が崩れる。ダービンワトソンでそれなら本当に独立がないのかどうかを検証する。
Fittedは予測値
Residualsは残差で、\(y_{i}-\hat{y_{i}}\)がいわゆる
つまり、残差と予測値をプロットした図になります。
x軸は回帰直線により予測されたyの値、y軸は予測値と観測値との差(残差)
よく資料などで誤差と残差を一緒で、残差の等分散性の均一と記載していたりするので、注意。
(まさにダービンワトソンも同じで、そういった仮定がある)
2.Normal Q-Q
あるデータの正規性、つまりあるデータが正規分布にしたがっている時、ちゃんと正規分布に従ってるよね?と確認するためのプロットです。
今回でいれば誤差がいわゆる正規分布に従っていると仮定しています。
なので、回帰診断法でプロットされるものとしては、誤差項についてになります。
正規Q-Qプロットです。
データが正規分布に従っている場合は、直線上に並ぶ。
▼ 重要
誤差は仮定として正規分布を仮定しています。そして実際に採れた誤差のデータの分布があります。この2つの分布が等しいか?というのを調べるためにこのQ-Qプロットがあります。
Q-Qプロットの縦軸がいわゆる実際の誤差の分布、そして横軸が誤差で仮定した分布です。
この2つをプロットすると同じ分布であれば、y=x上にデータが集まりますが、同じでない場合はばらけてしまいます。
残差分析で使用されるQ-Qプロットは、基本的にy=xを示す。
通常残差分析などで使用されたりしますが、普通誤差は標準正規分布に従っています。
つまり、0回りはすごいデータが集まっていて、そして左右に広がるにつれてデータが少なくなっていきます。
なので、残差分析のQ-Qプロットを表示させると、
yが0から1、xが0から1の範囲とするとき、
真ん中のx=0.5とy=0.5がいわゆる標準正規分布の原点周りを示すので、そこら辺にデータが集まります。
通常データは\(y=x\)上に集まるのが普通ですが、ずれるとその正規分布の仮定が多少ずれているということになります。
データが正規分布に従うと、点が直線上に並べられる。通常の回帰分析では、残差が標準正規分布に従うという仮定の下で行っている。
通常データが正規分布に従っていれば、以下のように単回帰であれば\(y=x\)上にデータが集約されます。
正規分布はそもそも真ん中近辺にデータが密集するので、実際にQ-Qプロットしても、真ん中あたりに集約されます。

3.Scale - Location
1,3は共にx軸はyの予測値で、y軸も実測値と予測値の残差に関するものです。
標準化残差(Standardized Residuals)はその名の通り、標準化した残差です。
これを実際に式に表すと以下のようになります。
各データiの標準化残差を\(e_{is}\)とし、各データの残差\(e_{i}\)の期待値が0で分散は\(s\)とすると、
\begin{eqnarray}
e_{is}
&=& \frac{e_{i} - E[e_{i}]}{V(e_{i})} \\
&=& \frac{e_{i}}{s}
\end{eqnarray}
となります。
nが大きくなると、残差の分散は誤差の分散\(\sigma^{2}\)に収束していきます。そしてこの不偏推定量として、
\begin{eqnarray}
s &=& \sqrt{ \frac{\sum_{i=1}^{n}e_{i}^{2} }{n-2} }
\end{eqnarray}
となります。
これを用いて、標準化残差を\( e_{is} = \displaystyle \frac{e_{i}}{s} \)とできます。
これを用いて、回帰診断図のScale - Locationは表現しており、
縦軸は、上記標準化残差に対して絶対値をとってルートを取った値です。そのため、0より大きい値でグラフは表示されています。
各データに対して標準化残差を出し、標準化残差の分布は標準正規分布となります。
標準化したということは、この分布は標準正規分布になります。
そのため、標準正規分布で考えた時、標準化残差が絶対値2.0を超えると、確率は0.023となり、ほぼ外れ値と認定できます。
標準化残差が全体的にバラけている、何か曲線に沿ってバラけているとかそういったことがない場合は、モデルの仮定である等分散性が保たれている証拠になります。
しかし曲線に沿って標準化残差がバラけているなどの場合は、相関があり、ランダマイズの分散性が保たれていないということになり、モデルの仮定である等分散性が保たれていないということになります。
これを残差分析などと言ったりします。
残差が曲線などに沿ってる場合は何かしらの相関があり分散の均一性がないなど検定するのが、ダービンワトソン比と呼ばれるものです。
よく誤差の系列相関を見るときに使われたりしますが、上でも説明した通り\(n\)が大きくなると誤差と残差は近しくなるので、同様に誤差でもダービンワトソンを考えることができます。
4.Residuals vs Leverage
赤い点線はCookの距離が0.5の位置を示す。
回帰式に与える影響の大きさ。これが0.5より大きいと外れ値の可能性があり、除いた方がよい。
leverage(てこ比)の値が0.5以上だと外れ値の可能性が高いので、除くが、これは説明変数を除くということではない。
ここでてこ比について考えます。
\(H\)ハット行列と言ったりもします。
この\(H\)がいわゆるてこ比になります。
このてこ比が実際に説明変数がそのデータの予測値に対してどのくらい影響を与えているかの指標になります。
実際にてこ比の式を見ると、x式が入っており、つまり各データがどのくらいてこ比に影響を与えているかがわかる。
xが変わることでてこ比の値も変わり、
てこ比は各データの予測値に対して、各説明変数がどのくらいその予測値に影響を与えているかを示すものになります。
通常回帰診断図の場合、
\(\hat{y_{i}} = h_{i}x_{i}\)となり1つの\(h_{i}\)が回帰診断図に可視化されてます。
そのため、この\(h_{i}\)つまりCook値が大きければ、外れ値の可能性がある、つまり\(x_{i}\)の値が外れ値の可能性があるので、除く必要があると判定できます。
https://www.sansakuro.com/046-regression-analysis/
通常回帰分析は以下のようになります。
各サンプルデータ \(y_{1}\), \(y_{2}\), \(y_{3}\),....
↓
↓これらのサンプルデータを用いて、、回帰モデル作成。つまりてこ比が作られる
↓
各データの予測値 \(\hat{y_{1}}\),\(\hat{y_{2}}\),\(\hat{y_{3}}\),...
つまり、サンプルデータに外れ値があると、その外れ値によってモデルの構築に影響があり、他のデータの予測値にも影響を及ぼす
ハット行列の対角成分がいわゆるてこ比になります。
実際に、各\(y_{i}\)が予測値\(\hat{y_{i}}\)に対してどのくらい影響度を持つか。
通常てこ比は0から1の値を取る。
外れ値であれば、その外れ値によってモデルにかなり影響を及ぼす。てこ比でその外れ値の影響度がかなり出る
\begin{eqnarray}
\hat{y_{}} &=& Hy \\
\hat{y_{1}} &=& h_{11}y_{1} + h_{12}y_{2} \\
\hat{y_{2}} &=& h_{21}y_{1} + h_{22}y_{2} \\
\end{eqnarray}

simplify statistic!
What is a Residuals vs. Leverage Plot? (Definition & Example)
\begin{eqnarray}
\beta &=& (X^{T}X)^{-1}X^{T}y \\
\hat{y_{}} &=& X\beta = X(X^{T}X)^{-1}X^{T}y \\
ハット行列 H &=& X(X^{T}X)^{-1}X^{T} \\
e &=& y - \hat{y_{}} \\
&=& y - X(X^{T}X)^{-1}X^{T}y \\
&=& (I_{n} - X(X^{T}X)^{-1}X^{T})y
\end{eqnarray}
誤差は期待値的には0なので、
\(\hat{y_{}}=X\hat{\beta_{}} + \epsilon\)ではなく、
\(\hat{y_{}}=X\hat{\beta_{}}\)ではなくとして考えた上で、
最小二乗推定量\(\beta\)を入れると、
\(\hat{y_{}}=X(X^{T}X)^{-1}X^{T}y\)
となります。
ここで\(H = X(X^{T}X)^{-1}X^{T}\)としたとき、この\(H\)をハット行列と言います。
命名としては、実測値である\(y\)から予測値の\(\hat{y_{}}\)にハットをつけて表記が一般的)に変換するため、ハット行列と言います。
線形代数の書き方だと\(H\)は写像になります。
てこ比
てこ比とは、あるデータ\(y_{i}\)が、どの程度同じデータの予測値\(\hat{y_{i}}\)に影響を与えているかを見る指標になります。
\(\hat{y_{}}= X \hat{\beta_{}} = X(X^{T}X)^{-1}X^{T}y \)と表せることから、
\(\hat{y_{i}} = h_{11}y_{1} + h_{22}y_{2} + \cdot + h_{ii}y_{i} + \cdot + h_{nn}y_{n} \)
となり、この時、\(y_{i}\)で偏微分すると、
\begin{eqnarray}
\frac{\partial }{\partial y_{i}} \hat{y_{i}} &=& h_{ii} \\
\end{eqnarray}
となり、\(h_{ii}\)は\(y_{i}\)が1単位変化した時の予測値\(\hat{y_{i}}\)の変化量とみることができます。微分することで1単位あたりの変化量と定義できます。
なのでこの値が大きいと、予測値\(\hat{y_{i}}\)に影響はもちろん、他の予測値にも影響を与えることが言えます。
そのため、この\(y_{i}\)は外れ値と考えることができます。
Cookの距離
Cookの距離とは、
\(①\) 全てのデータでの分析結果
\(②\) 全てのデータから1つデータを除いて、残りのデータでの分析結果
の差が大きいほど、その\(②\)で除いた1つのデータが影響度が高い、つまり外れ値と判定することができる。
この影響度のことをCookの距離と言います。
実際に見てみる
実際に以下でサンプルデータを用いて確認してみます!
Rによる統計解析の本のサンプルデータ使って!
通常、回帰診断図は説明変数が1つの単回帰モデルで使用されます。
回帰係数のt検定
回帰係数のt検定とは、
通常回帰係数はいくつかのデータから回帰係数を出しています。他で取れたデータから回帰係数を求めるとまた違った回帰係数が出ます。
となると取れたデータによって回帰係数はさまざまな値を取るということになります。
そのため、回帰係数も何回も行うことで幾つもの回帰係数を取得することができます。
となると、この回帰係数に対して検定をして有意水準で棄却できるか、有意性があるのかなどを検定して出すことができます。
つまり回帰係数を確率変数(統計量)と見立てて、検定を行うことができます。
そして検定をするには期待値と分散を求める必要があります。
期待値は簡単に求めれるので、母平均はわかります。
しかし分散については母分散はわからない。
そのため、t検定となります。つまり分散は不明なので、仮定して代用するのでまさに検定統計量はt分布になります。
t value t値。回帰係数=0(説明変数は目的変数に影響を与えない)であるという帰無仮説に対するt検定によって計算される値。