わかりやすい仮説検定とネイマンピアソンの定理

まずここではイカサマと仮定しているが、
イカサマの方がいいという判定になれば、このコインはイカサマと決定づけられるし、

施策を行った時に、
クリック率が上がったけど、これが奇跡的に偶然に結果が良かったのか、
それともやっぱ結果がよく上がったわけではなかったかを結論づける
https://note.com/hanaori/n/nc55ac8614799

そして帰無仮説は固定として考えます。
有意水準も固定の上考えるので、動かすのは対立仮説の方です。

帰無仮説は今回の結果との基準となる仮説のことです。
対立仮説は今回の試行の結果となる仮説のことです。
なので今回の試行の結果に有意性を持たせたいので、最終的には帰無仮説を棄却することを考えていきます。
 

例としては

• $①$ コインを投げた時、今回表が0.95の確率で出ている。通常は確率0.5なのに0.95出ているので、0.5を基準(帰無仮説)として、今回の0.95(対立仮説)を検定する。
• $②$ Webサイトの最適化をしたとき、コンテンツマーケティングでトップのキービジュアルを前の画像から今回の画像に変更したら10%滞在時間が増加した。なので前回を基準で、前回の画像(帰無仮説)から今回の画像(対立仮説)に変えた時の検定をする。
  (帰無仮説$H_{0}$: 滞在時間 = 0 ; 対立仮説$H_{1}$: 滞在時間 = 0.1)

ここでは、そんな仮説検定とネイマンピアソンの基本定理について、

仮説検定とは？
仮説検定で使われる用語として挙げられる「検定統計量・有意水準・P値」について、
棄却域や採択域から判定を誤る「第一種の錯誤と第二種の錯誤」について、
そしてネイマンピアソンの基本定理について
説明していきます。

仮説検定や信頼区間とは？

有意とはここまでの確率になったら流石になんか怪しいよね？
変なデータだよね？ってことをいうところ。
有意の5%に入ると、いかさまだ！ってなって棄却します。( $\alpha$に入ったら、帰無仮説を棄却してイカサマと認定する！)
 

有意水準を0.05に設定するということは、「5%以下の確率で起こる事象は、100回に5回以下しか起こらない事象だ。したがってこのようなまれな事象が起こった場合、偶然起こったものではないとしてしまおう」という意味です。したがって、P値が0.05（5%）を下回った場合、そのP値は偶然取る値ではないと結論付けられます。言い換えると、「極めて珍しいことが起こった」あるいは「何かしら意味があることである（＝“有意である“）」ということを表します。
この有意水準5%って実際はかなり稀な部類です。
 

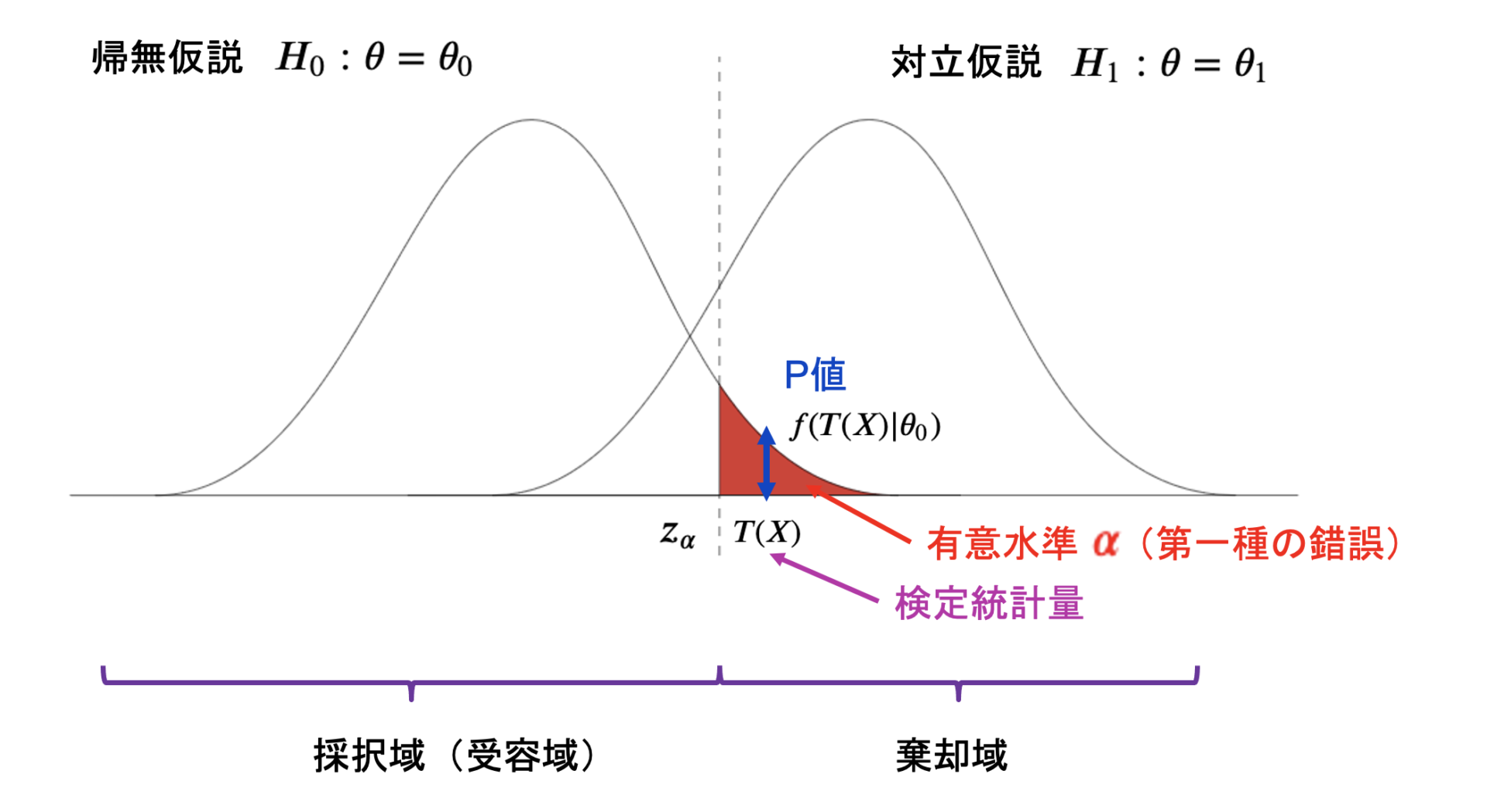
検定統計量、有意水準、P値について

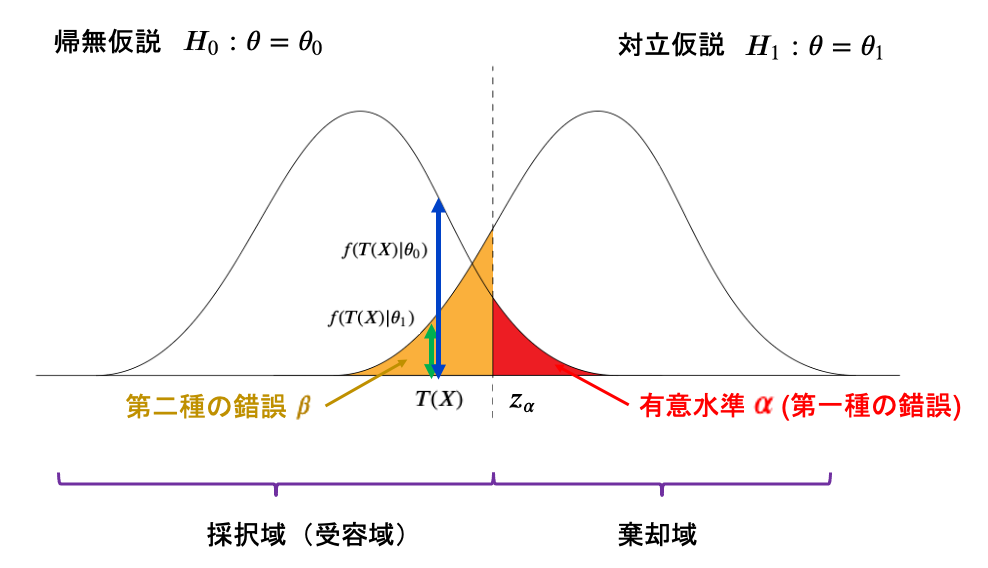
有意水準とは、帰無仮説の棄却域のこと。
検定統計量は、標本データから検定に使用するために計算した統計量のことで、この統計量で有意水準に含まれるかどうかで判定をしていく。この統計量が棄却域に入ったら、確率1で帰無仮説を棄却する。
P値は、帰無仮説において検定統計量が出る確率のこと。上記の図では帰無仮説の確率分布が$f(x|\theta_{0})$で表されるとした時、検定統計量$T(X)$が帰無仮説の分布から出る確率は$f(T(X)|\theta_{0})$となり、これがP値になります。
 

ここで確率密度関数の再度意味を考えよう！

棄却域

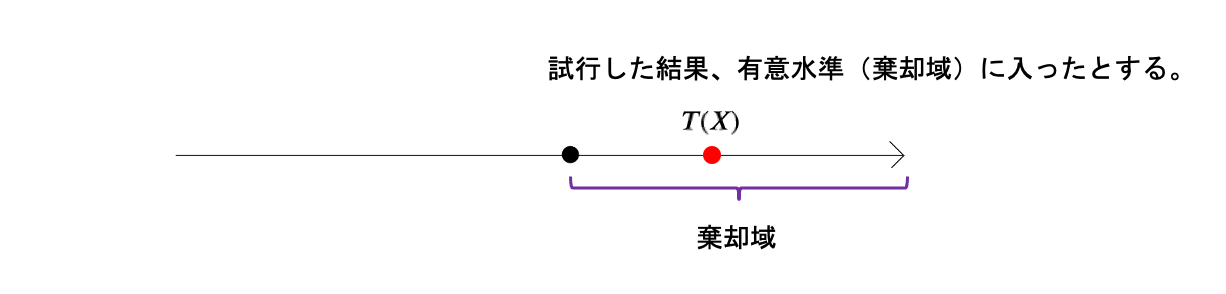
試行してみると、
結果的に検定統計量$T(X)$は、帰無仮説の棄却域である有意水準$\alpha$に入ったとします。

 

この時、
この$T(X)$は本当に奇跡で入ったのか、イカサマだったのかの確率がどのくらいかが大事になります。
確率密度関数は面積がその値の確率になります。
なので、
$T(X)$の値をとった時の、帰無仮説の密度関数$f(T(X)|\theta_{0})$と、対立仮説の密度関数$f(T(X)|\theta_{1})$から求めた確率を考えると、

上の図のようになります。
 

この1つ目の場合を、第一種の錯誤と言います。
まさにこれは有意水準のことを指します。

なぜなら、確率密度関数を考えてみてください。棄却域に$T(X)$が入った時、その$T(X)$が帰無仮説からでる確率は$f(T(X)|\theta_{0})$であり、
有意水準内での各$T(X)$の確率密度(確率)を合算すると、有意水準になるからです。
有意水準を$\alpha$とします。
 

採択域

そして有意水準は帰無仮説の棄却域です。
逆にそれ以外の箇所は帰無仮説の採択域(受容域）です。

 

そして試行してみると、
結果的に検定統計量$T(X)$が、帰無仮説の採択域に入ったとします。
 

 

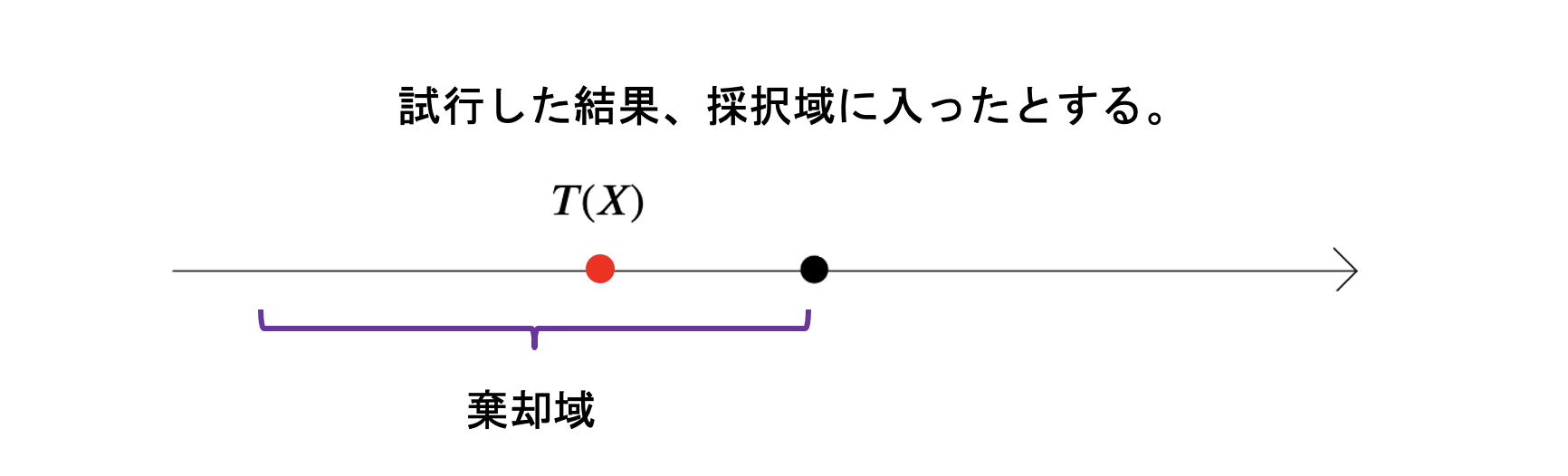
この時、帰無仮説の採択域では以下のようなことが考えられます。

この2パターンがあるかと思います。
 
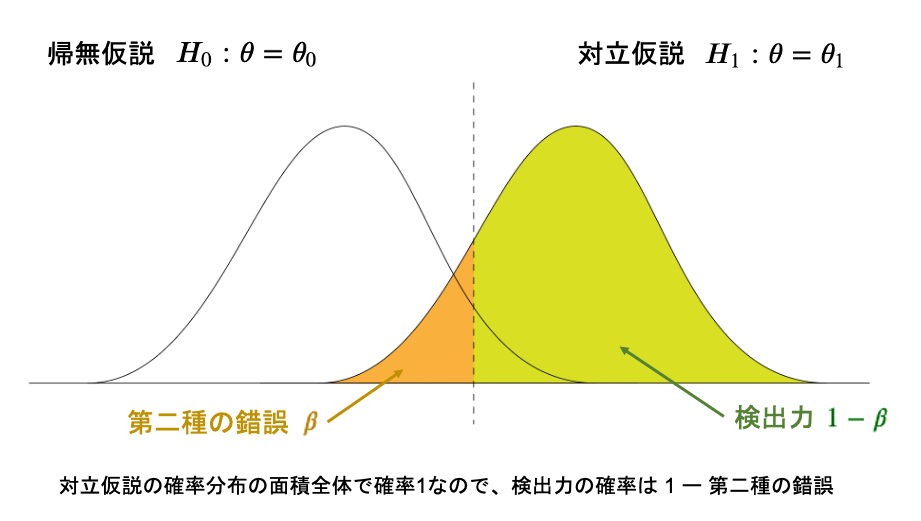
この1つ目の場合を、第二種の錯誤と言います。
この錯誤の確率を$\beta$とします。
ちなみに、2つ目の確率は$1-\alpha$になります。

そして図にすると、
対立で発生したものなのに、採択域なのでその確率としては以下の箇所です。

 

$f(T(X)|\theta_{0})$: 帰無仮説で検定統計量$T(X)$が出る確率
$f(T(X)|\theta_{1})$: 対立仮説で検定統計量$T(X)$が出る確率
を意味しています。

そして

を考えると、1つ目はまさに第二種の錯誤で確率は$\beta$ですが、
この2つの関係は余事象の関係から、2つ目の確率は$1-\beta$となります。
 

これが検出力と呼ばれるものです。結果的に正しいのであれば正しいと判定できる力ということですね。

ここまでの流れとしては、
まず棄却域(有意水準)から$\alpha$と定義され、
次に採択域から、$1-\alpha$、$\beta$が導かれ、
最後に検出力$1-\beta$が導かれました。
 

ネイマンピアソンの基本定理について

そして間違ってばっかな、第一種の錯誤である$\alpha$と、第二種の錯誤である$\beta$は、互いにトレードオフで、
$\alpha$が増えれば、$\beta$は減る
$\alpha$が減れば、$\beta$は増える
ので、両方小さくしたいができません。
間違っている判定なので両方小さくしたいですができません。
 

なので慣例的に、第一種の錯誤(有意水準)$\alpha$は固定にした状態（このくらいの誤りは許容するかー）にして、その上で第二種の錯誤$\beta$を以下に小さくするかを考えていきます。
 

でもいろんな検定・判定方法で一番小さくなるような判定方法はあるのでしょうか？

帰無仮説を$H_{0}: \theta = \theta_{0}$とし、対立仮説を単純対立仮説$H_{0}: \theta = \theta_{1}$とします。
そしてこの時、帰無仮説と対立仮説の関数をそれぞれ、$f(x|\theta_{0})$、$f(x|\theta_{1})$としてみます。
 

有意水準で$f(x|\theta_{1}) = kf(x|\theta_{0})$を満たす$k > 0$を置いたとき、
以下の図のように帰無仮説より対立仮説の分布が右側にあることを仮定した上で考えると、
その有意水準点より左側では帰無仮説と対立仮説の密度関数を用いた関係性は$\displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} > k$と表され、右側は$\displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} < k$と表されます。
 

ここで、リスクなのは第二種の錯誤なので、リスクのあるものに対して1を、リスクのないものに対しては0と置いて、間のものにおいては$r$( $0 < r < 1)$とすると、 以下のような検定を考えることができる。 そして検定の本質を思い出しましょう！

この本質を数式で考えて表してみましょう！
 

つまり、帰無仮説の分布において、
ある値が取れた時、左側である場合有意水準ではないので確率1で帰無仮説を採択する。
そして右側、つまり有意水準内の場合、確率0で帰無仮説を採択する(確率1で帰無仮説を棄却する)
ということになります。
 

そもそもこれって根本な話で、有意水準は帰無仮説を棄却するところなので、問答無用で確率1で棄却や！
で有意水準に入ってないのであれば、問答無用で確率が1で採択。
それを検定方式で以下のように表すことができます。
 

棄却を基準と見る検定を考えてみます。
連続分布とした場合、有意水準点より左側は採択域なので棄却は確率0、有意水準点より右側は棄却域なので棄却を確率1でします。
なので、この検定を数式で表してみると、
 
$$\begin{eqnarray} \delta(X) &=& \left\{ \begin{array}{l} 1, \quad if \quad \displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} \ge k \\ 0, \quad if \quad \displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} < k \\ \end{array} \right. \end{eqnarray}$$
 

と表現できます。
※ 連続分布の場合は$=$については$>$か$<$のどちらかにまとめてしまいます。上では$>$にまとめてます。
このように検定方式を定義することで、うまく有意水準の確率に落ち着くようになります。
 

実際にこの検定方式の期待値を取ってみると、
$$\begin{eqnarray} E[\delta(X)] &=& 1 \cdot P(\delta(X) = 1) + 0 \cdot P(\delta(X)=0) \end{eqnarray}$$
とすると、右辺は$1 \cdot P(\delta(X) = 1)$となり、採択域の部分の確率項は消え、棄却域となる確率の有意水準に等しくなります。
ここで、この期待値に対して有意水準$\alpha$とおくことで、有意水準を固定した時のぎりぎりのところを攻めて検出力が最大になるような検定方式となることが知られています。（照明は省略）
 

それがこの定理をネイマンピアソンの基本定理と呼びます。

まず、第一種の錯誤である$\alpha$を定めた上で、検定方式内の値を求めるような方法をとっています。これは元々の検定方式で、第一種の錯誤と第二種の錯誤はトレードオフなので、第一種の錯誤を固定とした上で検出力最大を目指すのが検定という仮定のもとに成り立っているのがわかる。
つまり、単純帰無仮説、単純対立仮説の時、上記の$\delta(X)$検定方法であれば、それが最強力検定、
つまり、単純帰無仮説、単純対立仮説の時、他の検定方法を考えても、上記の検定方法$\delta(X)$が一番検出力が最大となるということになります。
 
このネイマンピアソンの基本定理を用いて、導出される考え方として「尤度比検定」という最尤推定量を用いた検定方法があります。

離散の場合

帰無仮説の棄却域をαで固定にしているので、帰無仮説で考えます。つまり、$E_{\theta_{0}}[\delta(X)] = \alpha$で固定します。
なので、この期待値$E[\delta(X)]$は$\alpha$になることが想定できます。

 
離散の場合は、rは含めて有意水準点であればそこは調整で値を$r(0 < r < 1)$とし
$$\begin{eqnarray} \delta(X) &=& \left\{ \begin{array}{l} 1, \quad if \quad \displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} > k \\ r, \quad if \quad \displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} = k \\ 0, \quad if \quad \displaystyle \frac{f(x|\theta_{1})}{f(x|\theta_{0})} < k \\ \end{array} \right. \end{eqnarray}$$

なので、この期待値$E[\delta(X)]$は$\alpha$になることが想定できます。
そのため、$E[\delta(X)] = \alpha$と仮定します。
 

$$\begin{eqnarray} E[\delta(X)] &=& 1 \cdot P(\delta(X) = 0) + r \cdot P(\delta(X) = r) + 0 \cdot P(\delta(X)=0) \\ &=& \alpha \end{eqnarray}$$

上記の例は、片側対立仮説の場合の片側検定になります。
 

両側検定も同じような考え方で検定を構築することはできます。

この本質を数式で考えて表してみましょう！
片側検定では有意水準は右か左のどちらかにありましたが、今回は両方にあります。
なので数式で捉えると以下のような検定方式になるかと思います。
 

検定統計量が$T(X)$とした時、
そして有意水準点を$c, c'(0 < c_{+},c_{-} < 1)$として、$c_{-} < c_{+}$とした時、

$$\begin{eqnarray} \delta(X) &=& \left\{ \begin{array}{l} 1, \quad if \quad c_{-} < T(X) < c_{+}\\ r, \quad if \quad T(X) = c_{-} or T(X) = c_{+} \\ 0, \quad if \quad T(X) < c_{-} , c_{+} < T(X)\\ \end{array} \right. \end{eqnarray}$$
と表現できる。
 

離散の場合は、連続と違って、ピッタリ有意水準0.05となるような$E[\delta(X)]$は存在しません。
確率変数は1,2,3...のように離散となり連続ではないので、とびとびになり、2.345みたいな値でピッタリ有意水準が0.05になることもあります。
となると、連続では考えなかった$= k$の時を考える必要があるということになります。
 

▼お問合せはこちら