モンテカルロ法とは、
シミュレーションや数値計算を乱数を用いて行う方法の総称で、総称なのでさまざまなモンテカルロ法が世の中には存在しています。
さまざまな計算を乱数を用いて処理するような仕組みを提供するものになります。
よくある方法としては、円周率を計算する方法。
さらには棄却・受容サンプリングを用いると、サンプリングを用いて不明な分布のサンプリングを行います。
さらには重点サンプリング法を使うと、ある解析的に計算ができない積分計算を乱数を用いて近似計算を行うことができます。(これをモンテカルロ積分という)
さまざまな計算や課題などをサンプリングや乱数を用いて解決する手法全般のことですね!
モンテカルロ法
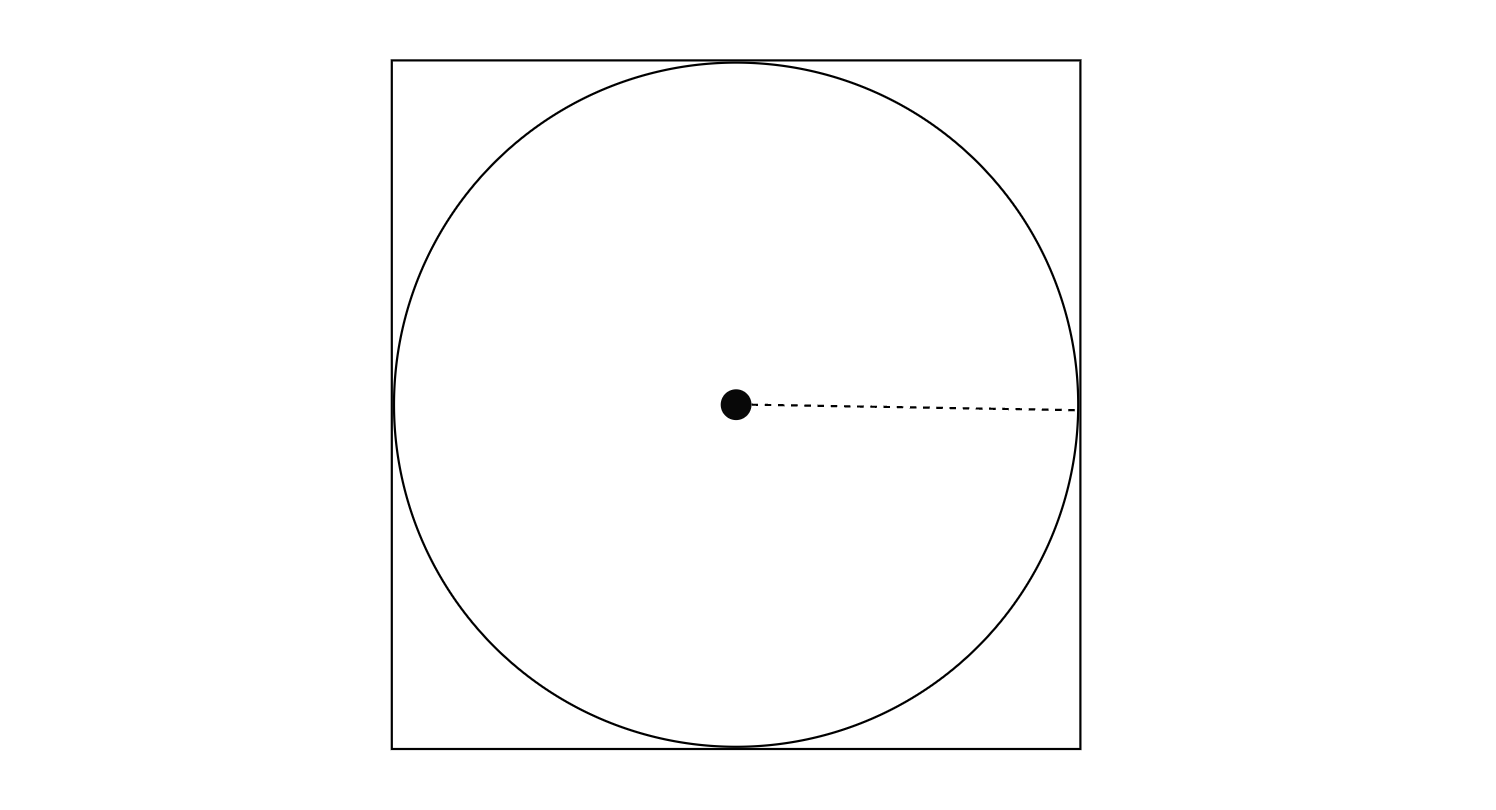
モンテカルロ法は、以下のような円を囲む正方形を用意します。
この正方形にランダムに乱数を出していきます。
とにかく乱数を乱れ打ちしていく。隙間無くなるくらいにもちろん重なりもなってよし!
以下のようなイメージです。
で正方形の中に円があって、その円の面積を求めたいとする。
そこで乱れ打ちの結果できた点を数えます。
正方形全体は乱数発生させた回数であり、\(N\)回
そしてその円の中に撃たれた回数が\(X\)回とすると、
正方形と円の撃たれた回数の比は\(X:N\)
つまり、これは正方形と円の面積比でもある。\(X:N\)
つまり、面積と当たった球の数は比例するって話ですね。
面積が大きければその分当たりやすくなるし、小さければその分当たりづらくなるしということです。
よって正方形の面積を\(S\)とすれば、円の面積は\(S \cdot \displaystyle \frac{X}{N}\)になる。
よって正方形の半径が\(R\)とすれば、逆算して\(Rπ = S \cdot \displaystyle \frac{X}{N}\) により、\(\pi\)がもとまる。
大数の法則によって、収束していくので、
数が多ければ精緻になっていく。
円の中隙間なく全体に撃たれるまではやる必要はなく、
正直少なくても問題はないが、その場合運良くそこに当たって、
円の中に100回、正方形と円の間の部分に3回とかだと面積比が100:103になるので明らかおかしい。
なので、大数の法則から数を増やせば増やすほどその運よくが調整されて、精緻になっていきます。
実際にプログラムで発生させてみる
こうなると難しい面積なども容易に求めることができそうである。
以下の方法はまさにこの乱数発生して、面積でサンプリングをしていく。
これが基本となる。
from scipy.stats.distributions import yulesimon_gen
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(7,7))
# サンプリング回数
total = 5000
# -1から1でサンプリング
x = (1 - (-1)) * np.random.rand(total) + (-1) # -1から1をランダムサンプリング
y = (1 - (-1)) * np.random.rand(total) + (-1) # -1から1をランダムサンプリング
# 中心(0,0)、半径1の円の作図
x_circle= np.linspace(-1, 1, 100)
y_up = np.sqrt( 1 - x_circle**2)
y_down = -np.sqrt(1 - x_circle**2)
plt.plot(x_circle, y_up, color='gray')
plt.plot(x_circle, y_down, color='gray')
i = 0
# 円の中に発生した乱数の数
cnt = 0
while i < total:
if x[i]**2 + y[i]**2 < 1: # 領域内に含まれるかどうかの判定
cnt = cnt + 1
plt.scatter(x[i], y[i], alpha=0.2, color='red')
else:
plt.scatter(x[i], y[i], alpha=0.1, color='blue')
i = i + 1
# プロットを範囲指定して出力
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.show()
print(cnt)
中心(0,0)、半径1の円である\(x^{2}+y^{2} = 1\)から、\(y = \sqrt{1 - x^{2}}, -\sqrt{1 - x^{2}}\)となるので、作図しています。
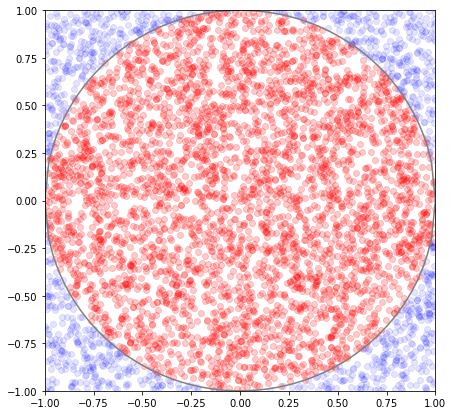
実行すると以下のように、正方形の範囲内で乱数を発生して、そのうち円の中で発生した乱数には赤色をつけています。
[-1,1]×[-1,1]の正方形内で発生した乱数の個数は5000個
そして、円の中に発生した乱数の個数は毎回サンプリングによって変わりますが、おおよそ3930個。
正方形の面積は2*2 = 4であり、乱数の個数で面積の比率を考えて、円の面積はおよそ4*3930/5000 = 4*0.786 = 3.144・・・\(①\)
普通に半径1の円の面積を求めると、1*1*\(\pi\) = \(\pi\)・・・\(②\)
よって、\(① = ②\)から、\(\pi\)はおよそ3.144と求めることができます。
これがいわゆるモンテカルロ法で、乱数の比率によって面積であったりさまざまな値を予測することができます。
そして以下が大事です。
しかし上の円のように、一旦正方形で中を囲んで、円の中に集まった乱数のみを抜き出せば、円からのサンプリングができます。
このようにして、難しい関数からサンプリングを可能にしたのが、モンテカルロ法になります。
そのさきのMCMC法はサンプリングした結果を事後分布だったり予測分布に適用して予測をするものになります。