わかりやすい標本平均と母平均、標本分散と母分散の関係

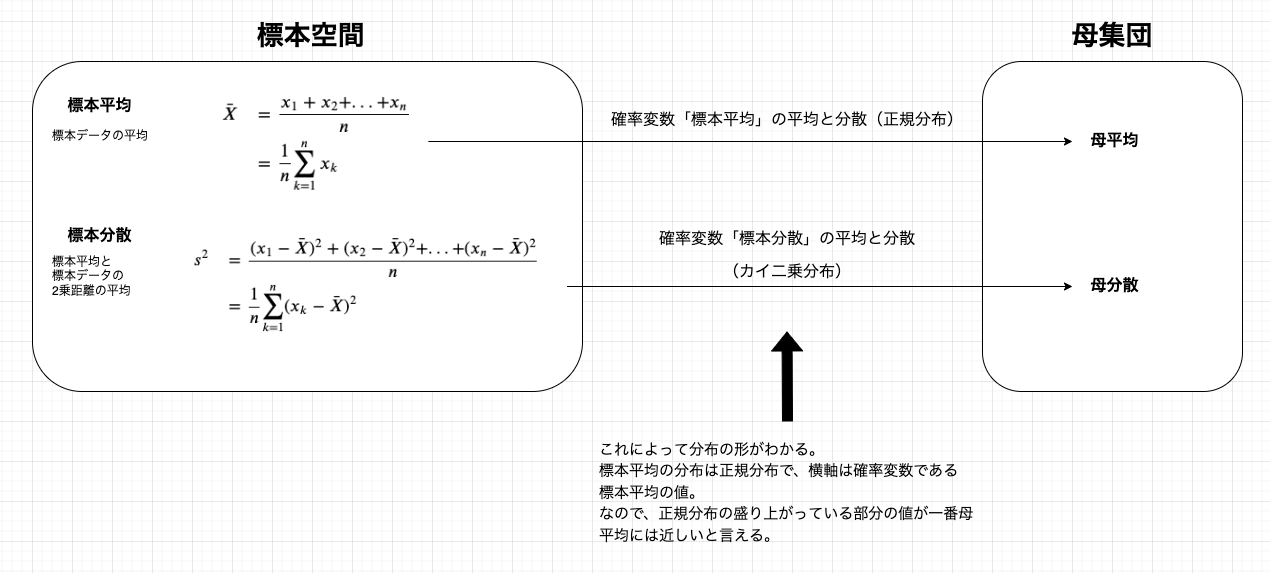
ここでは、標本平均と標本分散についてまとめていこうと思います。
標本平均とは、その名の通り標本データの平均です。
標本分散とは、その名の通り標本データの分散です。
実は統計学を勉強している方であればお分かりかと思いますが、区間推定や信頼区間を求める際に重要な要素になります。
できる限りわかりやすくまとめていこうと思います。
ここでは以下のようなことがわかります！

• 標本平均と標本分散の、それぞれの期待値の求め方がわかる
• 不偏分散、\(n-1\)で割ることの意味がわかる
• 標本平均が正規分布に、標本分散はカイ二乗分布に従うことがわかる

さらに統計学を学んでいく上で重要なこととして、
確率変数の統計量は確率変数になる。
ということです。
これを考えていくことで、統計学についての理解も深まっていくと思います！
この概念・考え方を学んでいきましょう！
 

ここでサンプルデータとして、
確率変数\(X\)が正規分布\(N(\mu, \sigma^{2})\)に従うと仮定すると、
\(X\)の期待値\(E[X]=\mu\), 分散\(V(X)=\sigma^{2}\)となります。
各確率変数は互いに独立とします。
ランダムでデータを出す際に、1つ前のデータによって今回のデータに影響を与えるものではないとして、独立と考えます。
この条件の下で考えていきます。

標本平均と母平均の関係について考えます

ここでは、まず標本平均を実際に求めてみたいと思います。
そのあと、母平均との関係性や、標本平均の分布について調べていきましょう。

そもそも標本平均とは

標本平均とは、その名の通りサンプリングで得られた標本データ(確率変数)の平均のことです。
定義としては、以下です。平均を\(\bar{X}\)とした時、
\begin{eqnarray}
\bar{X}　&=& \frac{x_{1}+x_{2}+...+x_{n}}{n} \\
&=& \frac{1}{n}{\sum_{k=1}^{n}x_{k}}
\end{eqnarray}
そのまんまですね。
この\(\bar{X}\)の期待値( \(n\)を大きくして行った時に収束する値)を求めてみましょう。
サンプルデータも毎回ランダムで発生するので、例えば最初に採れた\(n\)=100のデータでとった平均値と、次に採れた\(n\)=100のデータでとった平均値は毎回同じとは限りません。
そのため、この\(\bar{X}\)も確率変数になります。
ということは、確率変数なので、期待値や分散が存在しますし、さらに何回も\(\bar{X}\)を取得すればヒストグラムで書いて、確率密度関数や確率分布が存在するということになります。（これが最終目標！）
 

意外とない感覚ですが、大事なことです。確率変数というとサイコロの目などサンプリングで出てきた直接の値をイメージしがちですが、それらの確率変数に対して四則演算等して求めた値も確率変数になりますね！
 

標本平均の期待値を求める

まず\(\bar{X}\)の期待値\(E[\bar{X}]\)を求めます。
そのまんま期待値を取ると、
\begin{eqnarray}
E[\bar{X}] &=& \frac{E[x_{1}+x_{2}+...+x_{n}]}{n} \\
&=& \frac{E[x_{1}]+E[x_{2}]+...+E[x_{n}]}{n}　\\
&=& \frac{\mu+\mu+...+\mu}{n} \\
&=& \mu
\end{eqnarray}
となります。

標本平均の分散を求める

次に\(\bar{X}\)の分散\(V(\bar{X})\)を求めます。
これに関してもそのまま分散をとると、
そのまんま期待値を取ると、
\begin{eqnarray}
V(\bar{X}) &=& V \left(\frac{x_{1}+x_{2}+...+x_{n}}{n}\right) \\
&=& \frac{V(x_{1}+x_{2}+...+x_{n})}{n^{2}} \\
&=& \frac{V(x_{1})+V(x_{2})+...+V(x_{n})}{n^{2}}　\\
&=& \frac{\sigma^{2}+\sigma^{2}+...+\sigma^{2}}{n^{2}} \\
&=& \frac{n\sigma^{2}}{n^{2}} \\
&=& \frac{\sigma^{2}}{n}
\end{eqnarray}
となります。
以上のことから、
標本平均の期待値は、\(E[\bar{X}] = \mu\)
標本平均の分散は、\(V(\bar{X}) = \displaystyle \frac{\sigma^{2}}{n}\)
となります。
（平均と期待値が言葉に入り混じっていておかしくなる...)

標本平均の分布を求める

さらにここで、
標本平均の分布,確率密度関数を求めてみます。
一度標本平均の定義を振り返ってみます。
標本平均は以下の式で表されました。
\begin{eqnarray}
\bar{X}　&=& \frac{x_{1}+x_{2}+...+x_{n}}{n} \\
&=& \frac{1}{n}{\sum_{k=1}^{n}x_{k}}
\end{eqnarray}
実はこの式、、、中心極限定理の条件を満たしています。

ということは、\(n\)が無限大の時、正規分布に収束することがわかっています。
そのため、標本平均は正規分布に従うということになります。
よって期待値と分散は推定される母集団の値を示しており、\(n\)が無限大の時なので、
標本平均\(\bar{X}\)の分布は、正規分布\(\displaystyle N(\mu,\frac{\sigma^{2}}{n})\)に従うということになります。

標本平均\(\bar{X}\)は上記定義のサーメーションを展開すると、
\begin{eqnarray}
\bar{X}　&=& \frac{x_{1}+x_{2}+...+x_{n}}{n} \\
&=& \frac{S_{n}}{n}
\end{eqnarray}
となり、\(n\)が無限大\(n \rightarrow \infty\)とすると、右辺は中心極限定理により正規分布に従うので、当然左辺の標本平均も正規分布に従うということになるからです。
※ \(S_{n} = X_{1}+X_{2}+...+X_{n}\)で表されるようなものとして、二項分布があります。二項分布の各確率変数はベルヌーイ分布に従います。
ベルヌーイ分布は0,1の2値を取りますが、1を成功とした時、二項分布は\(S_{n}\)は\(n\)回のうちの成功回数になります。
二項分布も確率変数の和で表されるということから、\(n \rightarrow \infty\)とした時、つまり試行回数をものすごい増やした時、中心極限定理によって正規分布に収束していきます。
これを、二項分布の正規近似と呼んだりします。

ちなみに、二項分布に対して\(np = \lambda\)としたポアソン分布も、二項分布と同じ確率変数で確率変数の和で表現されます。
そのため、ポアソン分布も中心極限定理により正規分布に収束していきます。これを、ポアソン分布の正規近似と呼んだりします。

この性質があるから、信頼区間の問題では、正規分布や二項分布に従うデータの場合の信頼区間を構成するような問題が多いのです。

標本分散と母分散の関係を考えます

ここでもまず標本分散を実際に求め、そして母分散との関係性や、標本分散の分布について考えていきたいと思います。

そもそも標本分散とは

標本分散とは、その名の通りサンプリングで得られた標本データ(確率変数)の分散のことです。
標本データの分散なので、標本データの平均を用いて以下のように定義されます。
分散は平均からの距離なので、
\begin{eqnarray}
s^{2}　&=& \frac{(x_{1}-\bar{X})^{2}+(x_{2}-\bar{X})^{2}+...+(x_{n}-\bar{X})^{2}}{n} \\
&=& \frac{1}{n}{\sum_{k=1}^{n} (x_{k}-\bar{X})^{2}}
\end{eqnarray}

標本分散の期待値を求める

標本分散の期待値を求めます。
上記の定義に対してそのまま期待値をとっても計算できません。
イメージ、\(E[(x_{k}-\bar{X})^{2}]\)という形が想像できますが、
確率変数\(X\)の期待値は、\(E[X]=\mu\)であるため、分散に変換することができません。
なので\(\mu\)を入れてまず式変形させます。
\(-\mu+\mu\)をつけて、そして\((\bar{X}-\mu)^{2}\)は定数なので、外に出して
\begin{eqnarray}
s^{2}　&=& \frac{1}{n}{\sum_{k=1}^{n} (x_{k}-\mu+\mu-\bar{X})^{2}} \\
&=& \frac{1}{n}{\sum_{k=1}^{n} ((x_{k}-\mu)-(\bar{X}-\mu))^{2}} \\
&=& \frac{1}{n}{\sum_{k=1}^{n} ((x_{k}-\mu)^{2})} - \frac{2}{n}(\bar{X}-\mu)\sum_{k=1}^{n}(x_{k}-\mu) + \frac{1}{n}(\bar{X}-\mu)^{2}\sum_{k=1}^{n}1 \\
&=& \frac{1}{n}{\sum_{k=1}^{n} ((x_{k}-\mu)^{2})} - \frac{2}{n}(\bar{X}-\mu)\sum_{k=1}^{n}(x_{k}-\mu) + (\bar{X}-\mu)^{2}・・・① \\
\end{eqnarray}
ここで、\(①\)の第2項目の和について展開すると、
\begin{eqnarray}
\sum_{k=1}^{n}(x_{k}-\mu)　&=& (x_{1}-\mu)+(x_{2}-\mu)+...+(x_{n}-\mu) \\
&=& (x_{1}+x_{2}+...+x_{n})-n\mu \\
&=& n\bar{X}-n\mu \\
&=& n(\bar{X}-\mu) \\
\end{eqnarray}
となるので、\(①\)をさらに変形して、
\begin{eqnarray}
s^{2}　&=& ① \\
&=& \frac{1}{n}{\sum_{k=1}^{n} ((x_{k}-\mu)^{2})} - 2(\bar{X}-\mu)(\bar{X}-\mu) + (\bar{X}-\mu)^{2} \\
&=& \frac{1}{n}{\sum_{k=1}^{n} ((x_{k}-\mu)^{2})} - 2(\bar{X}-\mu)^{2} + (\bar{X}-\mu)^{2} \\
&=& \frac{1}{n}{\sum_{k=1}^{n} ((x_{k}-\mu)^{2})} - (\bar{X}-\mu)^{2} \\
\end{eqnarray}
確率変数\(X\)の期待値が\(\mu\)なので\(\mu = E[X]\)、標本平均\(\bar{X}\)の期待値が\(\mu\)なので\(\mu = E[\bar{X}]\)ということから、上の\(s^{2}\)に対して期待値\(E\)を取ると、
\begin{eqnarray}
E[s^{2}] &=& \frac{1}{n}{\sum_{k=1}^{n} E[(x_{k}-\mu)^{2}]} - E[(\bar{X}-\mu)^{2}] \\
&=& \frac{1}{n}{(n\sigma^{2})} - \frac{\sigma^{2}}{n} \\
&=& \frac{n-1}{n}{\sigma^{2}} \\
\end{eqnarray}
標本分散の期待値は、母分散を多少過小評価します。
そのため標本データを用いて母分散を推定したいとなると、少し推定がずれてしまうということになります。

不偏分散

上の式を\(\sigma^{2}\)について変形すると
\begin{eqnarray}
s^{2} &=& \frac{n-1}{n}{\sigma^{2}} \\
\frac{n}{n-1}s^{2} &=& \sigma^{2} \\
\frac{n}{n-1}{\frac{1}{n}{\sum_{k=1}^{n} (x_{k}-\bar{X})^{2}}} &=& \sigma^{2} \\
\frac{1}{n-1}{\sum_{k=1}^{n} (x_{k}-\bar{X})^{2}} &=& \sigma^{2} \\
\end{eqnarray}
となるので、
ここで左辺を\(U\)とすると、\(E[U]=\sigma^{2}\)が成立し、\(U\)は母分散\(\sigma^{2}\)の不偏推定量となります。
なので標本データから母分散を推定するとなると、標本分散ではなく\(U\)を用いて計算することの方がより良く推定ができるということです。

$$
U = \frac{1}{n-1}{\sum_{k=1}^{n} (x_{k}-\bar{X})^{2}}
$$
ちなみにこの\(U\)を不偏分散と呼びます。
不偏推定量となる分散っていう名前から不偏分散ですね。

標本分散の分布を求める

標本分散の確率分布は、カイ二乗分布になります。
ここでは示しませんが、
以下のような定理があります。

ここで標本分散の定義式を再掲します。
\begin{eqnarray}
s^{2}　&=& \frac{(x_{1}-\bar{X})^{2}+(x_{2}-\bar{X})^{2}+...+(x_{n}-\bar{X})^{2}}{n} \\
&=& \frac{1}{n}{\sum_{k=1}^{n} (x_{k}-\bar{X})^{2}}
\end{eqnarray}
この両辺に対して\(\sigma^{2}(>0)\)で割ると、
\begin{eqnarray}
\frac{s^{2}}{\sigma^{2}}
&=& \frac{1}{n} \lbrace \frac{(x_{1}-\bar{X})^{2}+(x_{2}-\bar{X})^{2}+...+(x_{n}-\bar{X})^{2}}{\sigma^{2}} \rbrace　\\
&=& \frac{1}{n} \lbrace {(\frac{x_{1}-\bar{X}}{\sigma})^{2}+(\frac{x_{2}-\bar{X}}{\sigma})^{2}+...+(\frac{x_{n}-\bar{X}}{\sigma})^{2}} \rbrace \\
&=& \frac{1}{n} \lbrace {{X_{1}}^{2}+{X_{2}}^{2}+...+{X_{n}}^{2}} \rbrace \\
\end{eqnarray}
右辺について
\begin{eqnarray}
X_{n} &=& \frac{x_{n}-\bar{X}}{\sigma}
\end{eqnarray}
と置いてますが、このようにすると、\(x_{n}\)の期待値が\(\bar{X}\)(正式には\(\mu\)だが、期待値とると同じ)で、分散が\(\sigma^{2}\)ということから、\(X_{n}\)は正規化され、右辺の各項目が正規化され2乗になっているということから、
各項目は標準正規分布\(N(0,1)\)に従います。
よって上の定理から、標本分散はカイ二乗分布に従います。

左辺の分母の\(\sigma^{2}\)は、母分散で定数なので無視。

ちなみに、左辺は信頼区間を勉強したことがある方であれば見たことあるって感じるかと思いますが、
分散の信頼区間を求める際に出てくる形になっています。
なので分散の信頼区間を求めるときは、このカイ二乗分布を用います。

まとめ

▼ お問合せはこちら