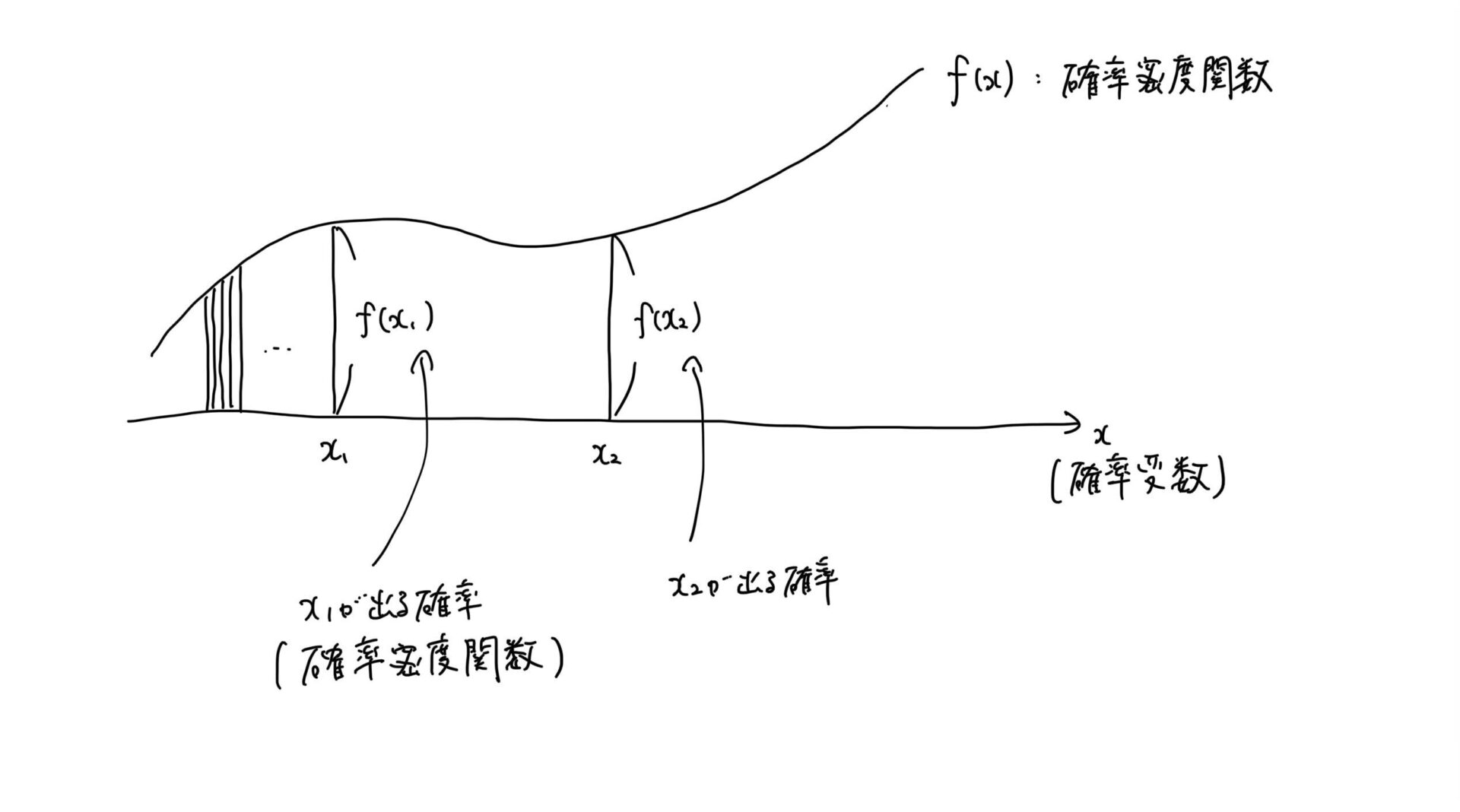
分布関数とは、確率変数の小さいところからの累積の関数になります。
確率関数と確率密度関数は同じ意味で、
ある確率変数が出る確率を示しています。
例えば、サイコロを1回投げたとします。
特に1が出やすいなどイカサマのない純粋なサイコロとすると、普通にどの目も確率1/6になります。
統計学の言葉で言うと、
確率変数が1は、1/6で出るということです。
この1/6が確率関数や確率密度関数です。
1/6は値ですが、関数なので厳密には確率変数の値がxとなる確率をxの関数で示したものが確率密度関数となります。
分布関数とは。
イメージ以下のようにするとなんとなくイメージが浮かんでくるのでは?
確率の線を足していくと、確率が足されていくイメージです。
例えば、
サイコロが1/6で出ます。これをグラフ化すると以下のようになります。
分布関数は確率変数の小さい値から積み上げていった確率の累積と話しました。
ということは、
例えばサイコロの目が1,2をたすと、2/6
1,2,3を足すと、3/6
になります。
離散分布は
サーメーション。シグマで表記し、
連続分布は、インテグラルで表記します。
インテグラルは、
でこの線を足していくので、イメージ
足していくとこの線が足されていくということはまさに面積になります。
今回のことから、
分布関数が分かれば、分布関数と確率密度関数や確率関数は積分の関係なので、
逆にいれば微分で算出することもできるという関係になります。
分布関数は確率を足していったこと、
そして確率は確率密度なので、
つまり分布関数は確率密度関数を足していったことということになります。
分布関数を\(F(x)\)、確率密度関数を\(f(x)\)とした時、
$$
F(x) = f(x_{1}) + f(x_{2}) + ... + f(x_{n}) ・・・①
$$
となります。
確率変数が離散値の場合はサーメーション、連続値の場合はインテグラルで表現されます。
サーメーションは1+2+...+nのように離散値を足していく場合に用いられる数学の記法で、
インテグラルは1,2,..のように飛び飛びではなく、連続する値を足していく場合に用いられる数学の記法です。
そのためそれぞれ記法に則って再度書くと、
離散分布は、
\begin{eqnarray}
F(x) &=& f(x_{1}) + f(x_{2}) + ... + f(x_{n}) \\
&=& \sum_{k=1}^{∞} f(x_{k}) \\
\end{eqnarray}
連続分布は、
\begin{eqnarray}
F(x) &=& f(x_{1}) + f(x_{2}) + ... + f(x_{n}) \\
&=& \int_{-∞}^{∞} f(x)dx \\
\end{eqnarray}
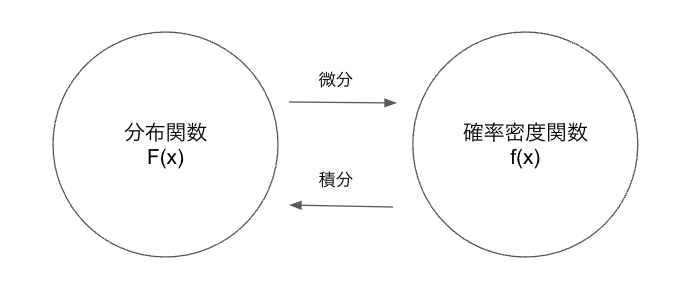
さらにこのことから、
積分と微分の関係から、
分布関数\(F(x)\)は確率密度関数\(f(x)\)の積分でもとまるため、
確率密度関数\(f(x)\)は分布関数\(F(x)\)の微分で求めることができます。
\begin{eqnarray}
f(x) &=& \frac{d}{dx}F(x) \\
&=& F'(x) \\
\end{eqnarray}
なので、何か問題とかで分布関数がわかっている時、確率密度関数を求める必要がある場合は、
微分をすることで簡単に求めることができます。
微分ができるのは連続する値の場合であり、
そのため離散値をとるサーメーションに対して微分を行うことができません。
なので、この関係は確率変数が連続値となる確率密度関数に対してのみ行うことができます。
確率密度関数を出すことで、
期待値や分散を求めることが可能になったりするので、
そういう意味でも常に確率密度関数を出すことは頭に置いておくのはいいかもですね。
2次元の場合の分布関数を考えてみます。
当然2次元になっても分布関数は確率密度関数の積み上げ、そして確率密度関数は確率を表します。
$$
F(x) = \int_{-∞}^{∞}\int_{-∞}^{∞} f(x,y)dxdy
$$