Contents
ベータ分布の確率密度関数
\(X\)を0から1をとる確率変数としたとき、
\begin{eqnarray}
f(x|\alpha, \beta) &=& \frac{ x^{\alpha-1}(1-x)^{\beta-1} }{Beta(\alpha, \beta)} \\
Beta(\alpha, \beta) &=& \displaystyle \int_{0}^{1} x^{\alpha-1}(1-x)^{\beta-1}dx
\end{eqnarray}
正規化定数(上の式を全てのxに対して積分)
\(Beta(\alpha, \beta)\)を計算してみます。簡単にするために、以下で計算します。部分積分をして、
\begin{eqnarray}
I(\alpha, \beta)
&=& \displaystyle \int_{0}^{1} x^{\alpha}(1-x)^{\beta}dx \\
&=& \bigl[ \frac{x^{\alpha+1}}{\alpha+1} \cdot (1-x)^{\beta} \bigr]_{0}^{1} - \int_{0}^{1} \frac{x^{\alpha+1}}{\alpha+1} \cdot \beta(1-x)^{\beta+1}(-1)dx \\
&=& \bigl[ \frac{x^{\alpha+1}}{\alpha+1} \cdot (1-x)^{\beta} \bigr]_{0}^{1} + \frac{\beta}{\alpha+1} \int_{0}^{1} x^{\alpha+1} \cdot (1-x)^{\beta+1}dx \\
&=& (0-0) + \frac{\beta}{\alpha+1}I(\alpha+1, \beta-1) \\
&=& \frac{\beta}{\alpha+1}I(\alpha+1, \beta-1)
\end{eqnarray}
この\(I(\alpha, \beta)\)に対して、繰り返し処理をして、
\begin{eqnarray}
I(\alpha, \beta)
&=& \frac{\beta}{\alpha+1}I(\alpha+1, \beta-1) \\
&=& \frac{\beta}{\alpha+1} \cdot \frac{\beta-1}{\alpha+2} I(\alpha+2, \beta-2) \\
&=& \frac{\beta}{\alpha+1} \cdot \frac{\beta-1}{\alpha+2} \cdot \frac{\beta-2}{\alpha+3} I(\alpha+3, \beta-3) \\
&=& \cdot \cdot \cdot \\
&=& \frac{\beta}{\alpha+1} \cdot \frac{\beta-1}{\alpha+2} \cdot \frac{\beta-2}{\alpha+3} \cdot \cdot \cdot \frac{1}{\alpha+\beta} I(\alpha+\beta, 0) \\
\end{eqnarray}
ここで、
\begin{eqnarray}
I(\alpha+\beta, 0)
&=& \int_{0}^{1} x^{\alpha+\beta}(1-x)^{0}dx \\
&=& \int_{0}^{1} x^{\alpha+\beta}dx \\
&=& \bigl[ \frac{x^{\alpha+\beta+1}}{\alpha+\beta+1} \bigr]_{0}^{1} \\
&=& \frac{1}{\alpha+\beta+1}
\end{eqnarray}
となるので、
\begin{eqnarray}
I(\alpha, \beta)
&=& \frac{\beta}{\alpha+1} \cdot \frac{\beta-1}{\alpha+2} \cdot \frac{\beta-2}{\alpha+3} \cdot \cdot \cdot \frac{1}{\alpha+\beta} \cdot \frac{1}{\alpha+\beta+1} \\
&=& \frac{\beta!}{(\alpha+\beta+1)(\alpha+\beta)\cdot\cdot\cdot(\alpha+3)(\alpha+2)(\alpha+1)} \\
&=& \frac{\alpha!}{\alpha!} \cdot \frac{\beta!}{(\alpha+\beta+1)(\alpha+\beta)\cdot\cdot\cdot(\alpha+3)(\alpha+2)(\alpha+1)} \\
&=& \frac{\alpha!\beta!}{(\alpha+\beta+1)!} \\
\end{eqnarray}
そして、\(\alpha \rightarrow \alpha-1, \beta \rightarrow \beta-1\)として、
\begin{eqnarray}
Beta(\alpha, \beta) &=& \frac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!}
\end{eqnarray}
となります。
\begin{eqnarray}
I(\alpha, \beta) &=& \frac{\alpha!\beta!}{(\alpha+\beta+1)!}
\end{eqnarray}
ベータ分布の期待値
上で求めた\(I(\alpha, \beta)\)を用いて計算をします。
\begin{eqnarray}
E[X] &=& \int_{0}^{1} xf(x|\alpha, \beta)dx \\
&=& \frac{1}{Beta(\alpha, \beta)} \int_{0}^{1} x^{\alpha}(1-x)^{\beta-1} dx \\
&=& \frac{1}{Beta(\alpha, \beta)} I(\alpha, \beta-1) \\
&=& \frac{(\alpha+\beta-1)!}{(\alpha-1)!(\beta-1)!} \cdot \frac{\alpha!(\beta-1)!}{(\alpha+\beta)!} \\
&=& \frac{\alpha!}{(\alpha-1)!} \cdot \frac{(\alpha+\beta-1)!}{(\alpha+\beta)!} \\
&=& \alpha \cdot \frac{1}{\alpha+\beta} \\
&=& \frac{\alpha}{\alpha+\beta} \\
\end{eqnarray}
ベータ分布の分散
こちらも、\(I(\alpha, \beta)\)を用いて計算をしますが、まず\(E[X^{2}]\)を求めた上で、分散公式\(V(X) = E[X^{2}]-{E[X]}^{2}\)を使って分散を求めます。
\begin{eqnarray}
E[X^{2}] &=& \int_{0}^{1} x^{2}f(x|\alpha, \beta)dx \\
&=& \frac{1}{Beta(\alpha, \beta)} \int_{0}^{1} x^{\alpha+1}(1-x)^{\beta-1} dx \\
&=& \frac{1}{Beta(\alpha, \beta)} I(\alpha+1, \beta-1) \\
&=& \frac{(\alpha+\beta-1)!}{(\alpha-1)!(\beta-1)!} \cdot \frac{(\alpha+1)!(\beta-1)!}{(\alpha+\beta+1)!} \\
&=& \frac{(\alpha+1)!}{(\alpha-1)!} \cdot \frac{(\alpha+\beta-1)!}{(\alpha+\beta+1)!} \\
&=& \alpha(\alpha+1) \cdot \frac{1}{(\alpha+\beta+1)(\alpha+\beta)} \\
&=& \frac{\alpha(\alpha+1)}{(\alpha+\beta+1)(\alpha+\beta)} \\
\end{eqnarray}
よって、分散公式から、
\begin{eqnarray}
V(X)
&=& E[X^{2}] - {E[X]}^{2} \\
&=& \frac{\alpha(\alpha+1)}{(\alpha+\beta+1)(\alpha+\beta)} - \frac{\alpha^{2}}{(\alpha+\beta)^{2}} \\
&=& \frac{\alpha(\alpha+1)(\alpha+\beta) - \alpha^{2}(\alpha+\beta+1) }{(\alpha+\beta+1)(\alpha+\beta)^{2}} \\
&=& \frac{\alpha\beta}{(\alpha+\beta+1)(\alpha+\beta)^{2}} \\
\end{eqnarray}
ベータ分布と二項分布の関連性、確率密度関数の直感的な意味
ベータ分布は、\(x(1-x)\)で\(x\)を0から1の間の値を取るので、
\(x(1-x)\)の形式、何かに似てますね!
そう、二項分布です!
二項分布ではよく確率を\(p\)として、\(p^{x}(1-p)^{n-x}\)で表示されますが、
ベータ分布では確率変数\(x\)がいわゆる\(p\)になります。
ベータ分布は、成功した回数をアルファ、失敗した回数をベータとしてさまざまな分布の形に変わります。
成功した回数、失敗した回数、、つまり2つの状態があるのでベルヌーイ分布や二項分布と何か関係性があるとわかるでしょう。
ベータ分布の関数の形からも、
二項分布に関係しているので、
二項分布に関係していて、アルフとベータがあって、\(x\)は0から1と覚えておけば、簡単にベータ分布の関数の形式が思い出せるようになるでしょう!
ベータ分布のグラフ
ベータ分布はさまざまな形を作ります。
確率変数\(x\)は成功する確率です。
アルファは成功した回数になるので、これに対応します。
アルファが0なら、成功していないので、xは0になります。
そしてxが1は、全て成功する場合になります。
なので、グラフで言うと、
アルファ>ベータだと、右側(1側)に傾聴したグラフになり、
アルファ<ベータだと、左側(0側)に傾聴したグラフになっていきます。
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16,10))
# [0, 1]で0.1刻みの値を作成
x = np.linspace(0, 1, 101)
# β分布の値作成
plt.subplot(331)
a = 1
b = 1
y = beta.pdf(x, a, b)
plt.plot(x, y, label=f"{a=}, {b=}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()
plt.subplot(332)
a = 2
b = 2
y = beta.pdf(x, a, b)
plt.plot(x, y, label=f"{a=}, {b=}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()
plt.subplot(333)
a = 3
b = 3
y = beta.pdf(x, a, b)
plt.plot(x, y, label=f"{a=}, {b=}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()
plt.subplot(334)
a = 7
b = 3
y = beta.pdf(x, a, b)
plt.plot(x, y, label=f"{a=}, {b=}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()
plt.subplot(335)
a = 3
b = 7
y = beta.pdf(x, a, b)
plt.plot(x, y, label=f"{a=}, {b=}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()
plt.subplot(336)
a = 300
b = 50
y = beta.pdf(x, a, b)
plt.plot(x, y, label=f"{a=}, {b=}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()
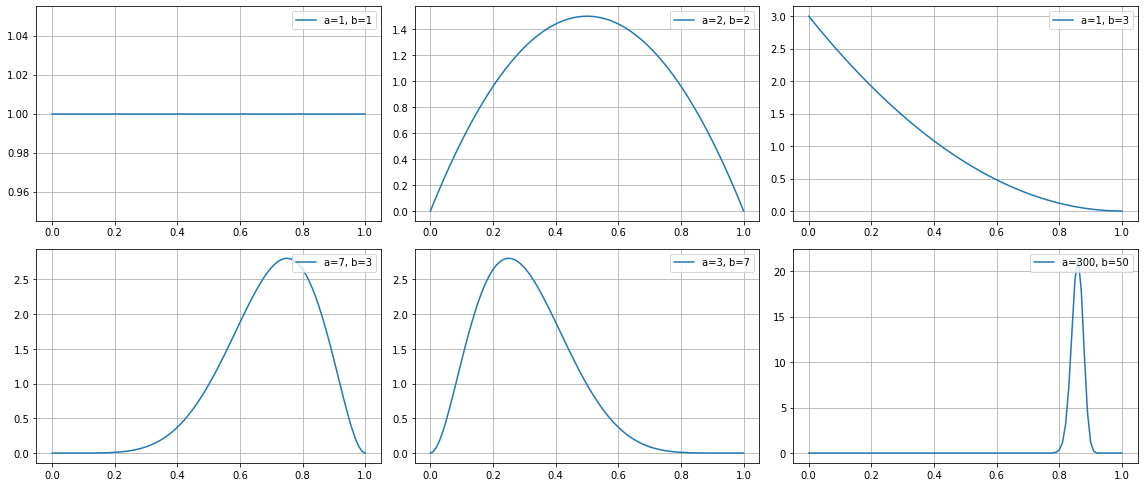
これを実行してみると、以下のようなグラフになります!
左上のグラフ
左上の図では、アルファ/ベータがそれぞれ1で、成功回数と失敗回数は0で、試行回数が0です。
この時、まだ成功確率なんてわからないので、一様分布になります。
真ん中上のグラフ
真ん中上の図では、アルファは2で、ベータも2で、成功した回数と失敗した回数がそれぞれ1で同じ状態になります。
この時点でもうすでに1回ずつは成功と失敗が出ており、すでに成功が1回出ているので、ここから何回も試行してずっと失敗だったとしても、成功する確率\(x\)が0になることは100%ありません。
さらにすでに失敗が1回出ているので、ここから何回も試行してずっと成功だったとしても、成功する確率\(x\)が1になることは100%ありません。
そのため、\(x = 0, 1\)は確率的に0%で確率分布は0になります。
右上のグラフ
右上の図では、アルファが1で、ベータが3で、成功した回数が0、失敗した回数が2です。
この時、2回の試行で成功は0回なので、成功確率は0です。2回の試行で失敗は2回なので、失敗確率は1です。
そのため、右上のような図になります。
左下のグラフ
左下の図では、アルファは7で、ベータは3で、成功した回数の方が多いです。
そうすると、試行回数が10回のうち成功が7回なので、この時成功確率は0.7となります。
実際グラフを見てみると、だいたい0.7あたりで盛り上がっているのがわかりますね!
真ん中下のグラフ
真ん中下の図では、アルファは3で、ベータは7で、失敗した回数の方が多いです。
そうすると、試行回数が10回のうち成功が3回なので、この時成功確率は0.3となります。
実際グラフを見てみると、だいたい0.3あたりで盛り上がっているのがわかりますね!
右下のグラフ
右下の図では、アルファは300で、ベータは50で、成功した回数の方が多いです。
そうすると、試行回数が10回のうち成功が3回なので、この時成功確率は0.3となります。
実際グラフを見てみると、だいたい0.3あたりで盛り上がっているのがわかりますね!
でも左下と同じように、0からどんどん上がっていくのではなく、0.6くらいで一気に伸びています。
これは最初の試行回数10回だと取れたデータが少なすぎて正確性がなく、まだ0.2や0.3などの可能性が残されているため、少し盛り上がっています。
しかし試行回数が増えると、大数の法則からもどんどん確率は収束していくので、300vs50まできたら、もうここから成功確率が0.2や0.3になることはほぼないだろうとなっています。なので低空飛行で0.6くらいから盛り上がっています。300vs50から、ここから一気に失敗が奇跡的に盛り返すみたいなことがない限り0.3などになりませんからね。
上のように、アルファの値やベータの値が更新されていくたびに、ベータ分布のグラフの形状はどんどん変わっていきます。
アルファ、ベータは、それぞれ成功した回数、失敗した回数。
つまり試行回数をどんどん増やしていくと、アルファ、ベータの値もどんどん増えていき、ベータ分布の形状はどんどん変わっていくので、
新しいデータが取れるたびに、それを取り込んでベータ分布を更新していきます。
ベータ分布はこのようにどんどんデータが取れるたびに更新していき、試行回数がかなり増えると形状も収束していきます。
このようにしていくのはまさに、ベイズ更新に似ているもので、ベイズ更新でもよく扱われる関数となります。