わかりやすい最尤法

データを分析していくにはまずデータをサンプリングしていきます。
そして繰り返し得られたデータがどんな確率分布なのかを知る必要があるかと思います。
どういった分布でこのデータが発生されているのか。
その分布を関数で導き出すことで、将来の分布や母集団を推定する役にも立ったりします。
今回はその得られたサンプルデータ（標本データ）が、どういった確率分布から得られたものなのかを推定する方法である、「最尤法」について話していきたいと思います。
このページでは以下のようなことを知ることができます。

• 最尤法とは？
• 最尤法のそもそもの原理
• 最尤法を用いたパラメータ推定（最尤推定量）

 

サンプルデータのヒストグラム

さまざまな密度関数にはパラメータが存在する。
そのパラメータの値によってその密度関数はいろんな形をする。

そして幾つかのサンプルデータが得られたとする。
例えば、以下のような確率変数が得られたとする。
1,2,6,2,2,4,3,3,8,9

（足りなければもっとブートストラップとかで出す)

なんとなく、この値だけを見ると、2が4回で、3が2回出ていて、それ以外は1回なので、
ヒストグラムで書くと左に盛り上がったグラフになりそうな予感！
その線を引いていくと、それが標本分布であり、サンプルデータからの確率密度関数になる。
そしていろんな要素で確率密度関数を仮定する。

• 1. 有名な確率密度関数の定義から、その確率密度関数が成立する事象と照らし合わせて、それに近しいものを選択する
• 2. 左右対称であれば正規分布かt分布、などのようにこういったグラフの形なら、この確率密度関数が合うだろうという風に選択する

今回は左寄りなので、
ベータ分布に近い形だなーってなるので、ベータ分布から発生したデータだと仮定します。(ベータ分布が確率密度関数と仮定)
最尤法では、もっともらしいパラメータを求めます。
今あるデータでこれがどう言った分布から発生されたデータなのかを推定したいですよね。
その発生となる確率分布を求めるのが最尤法で、つまりデータの発生源のメカニズムを特定するみたいなイメージです。
例えば、今1,1,2,2,2,3,3,3,4,5,....が得れたら、
2や3が出るから左側に重心のある確率分布なのかなーと想像できます。

 

 

 

掛け算で尤度の計算を行う

同時にこれらのデータが取れたということは、
「同時に起きた」
ということなので、確率の積の公式と、
確率密度関数は確率なので、
確率密度関数の掛け算を行います。
そしてそれらは同時に発生するので、
確率の積の公式によって、同時に発生するものは確率をかけるので、
尤度とは、確率分布(確率)の掛け算のことです。
例えば1次元のサンプルデータが、\(x_{1},x_{2},...\)と取れたとします。
それらのデータが正規分布\(N(\mu,\sigma^{2})\)に従っていると仮定した時、
\(x_{1}\)が出る確率は\(f(x_{1}|\mu,\sigma^{2})\)となります。
\(x_{1},x_{2},...\)のデータは同時に出たので、積の公式により
尤度は、Likelihoodという単語で、\(L\)を用いて
$$
L(\mu,\sigma^{2}) = f(x_{1}|\mu,\sigma^{2}) * f(x_{2}|\mu,\sigma^{2}) * ...
$$
となります。
そして、最尤法は「最も(もっとも)尤もらしい(もっともらしい)」確率密度関数を出すことです。
なので、上記の尤度を計算して尤度が最大となるときのパラメータ（尤もらしいパラメータ）を求めます。

得られたデータからこういう密度関数が出来上がるのでは？
となり、その仮定した確率密度関数でその確率を出して、
それを最大化する。
それが最尤法です。
よく出る確率変数の値は、当然確率も高くなるよね。という考えのもと、もっともらしいと考える。

 

 

尤度が最大になるパラメータを求める

最尤法を扱うと、対数尤度関数という言葉が出てきたりします。
対数尤度関数とはその名の通り、尤度に対して自然対数をとった関数のことです。
尤度は確率の掛け算で、確率は常に正の値を取るため、尤度は正の値を取ります。
そのため尤度に対して自然対数を取ることができます（わからない人は数2勉強)
自然対数\(\log(x)\)の\(x\)は常に0より大きい値になります。
尤度は常に0より大きい値なので、自然対数をとって、\(\log(尤度)\)とできるわけです。
この\(\log(尤度)\)のことを、対数尤度関数といい、求めるパラメータを\(\theta\)として\(l(\theta)\)と表します。
$$
l(\theta) = log(尤度)
$$

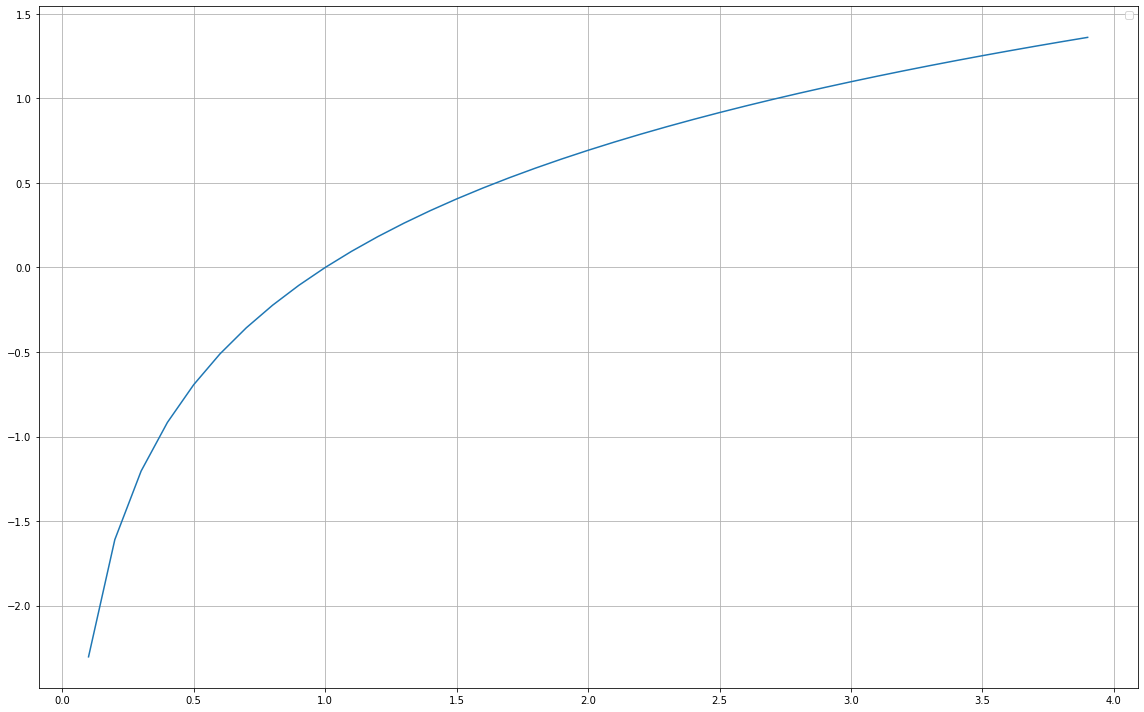
ここで自然対数をグラフにすると以下のようになります。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta

fig = plt.figure(figsize=(16,10))

# サンプルデータ生成
x = np.arange(0.1, 4, 0.1)
y = np.log(x)

plt.subplot(111)
plt.plot(x, y)
plt.legend(loc="upper right")
plt.tight_layout()
plt.grid()

自然対数は、x軸の正の部分では自然対数\(\log(x)\)は単調増加なのでxの値が大きくなるほど、どんどん自然対数の値は増加していきます。
つまり尤度に対して自然対数をとっても常に尤度が最大→自然対数が最大
ということになります。
そのため自然対数をとった対数尤度関数で最大となるパラメータを求めることに問題が帰着されます。
でも自然対数をとらず、そのまま尤度を最大化すればいいじゃんと思いますが、
そうすると計算がかなり複雑になってしまいます。
自然対数をとることで、掛け算を足し算に直して計算することができるため、計算の簡略化ができます。
$$
\log(ab) = \log(a) + \log(b)
$$

そして掛け算をするとどうしても、サーメーションが出たりすると計算が難しくなる。
そのため、掛け算をした確率は必ず正の値を取るため、対数をとることができるので、
logをとって計算する。
これにより掛け算が和で計算可能になり楽になります。
 

 

そして対数尤度に対して、求めたいパラメータで偏微分を行い、
偏微分方程式でパラメータを求めることでパラメータの推定ができます。
パラメータの個数分の偏微分方程式を作成しないと、解は一意に求まりません。
パラメータが\(x_{1}, x_{2}\)の2つがあったとして、
\(x_{1} + x_{2} = 3\)
という式が得られたとする。
1つの式しかないので、必ず一意で\(x_{1}, x_{2}\)の値は求まりません。
例えば、\(x_{1}\)が2だとすれば、\(x_{2}\)は1となります。
さらに\(x_{1}\)が10000だとすれば、\(x_{2}\)は-9997となります。
このように、それぞれ値が定まらなくなってしまいます。

 

ここで、確率変数\(X\)の分布を正規分布とした時の尤度を求めたいと思います。
データ\(x_{1}, x_{2}, x_{3}, ..., x_{n}\)が取れたとし、さらにこれらが正規分布\(N(\mu, \sigma^{2})\)に従っていると仮定します。
そうした時、尤度は
\begin{eqnarray}
l(\mu, \sigma^{2})　&=& \frac{1}{\sqrt{2\pi\sigma^{2} }}{\exp \lbrace \frac{(x_{1}-\mu)^{2}}{2\sigma^{2}} \rbrace} * \frac{1}{\sqrt{2\pi\sigma^{2} }}{\exp \lbrace \frac{(x_{2}-\mu)^{2}}{2\sigma^{2}} \rbrace} * ... \\
&=& \Bigr(\frac{1}{\sqrt{2\pi\sigma^{2} }}\Bigr)^{n} \exp\Bigr( \frac{(x_{1}-\mu)^{2}}{2\sigma^{2}} + \frac{(x_{2}-\mu)^{2}}{2\sigma^{2}} + ...\Bigr) \\
&=& \Bigr(\frac{1}{\sqrt{2\pi\sigma^{2} }}\Bigr)^{n} \exp\Bigr( \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^{2}} \Bigr)
\end{eqnarray}
となります。
指数関数の足し算などを用いてますね。

 

そしてこれに対して最大値を求めるので、パラメータである\(\mu\)と\(\sigma\)の偏微分=0を満たす\(\mu\)と\(\sigma\)の組を求めますが、
上記の尤度\(l(\mu, \sigma^{2})\)を見ると、指数関数があったりして微分などして計算がどうも難しそうになります。

 

そこで、尤度>0なので、対数をとってみると、(計算式の展開は数2など見てください)
\begin{eqnarray}
L(\mu, \sigma^{2})
&=& \log(l(\mu, \sigma^{2})) \\
&=& \log( (\frac{1}{\sqrt{2\pi\sigma^{2}}})^{n} \exp( \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^{2}} ) ) \\
&=& n\log(2\pi\sigma^{2})^{-\frac{1}{2}} + \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^{2}} \\
&=& -\frac{n}{2}{\log(2\pi\sigma^{2})} + \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\sigma^{2}}
\end{eqnarray}
となり、指数関数もなくなり、ある程度使いやすくなりました。

 

正規分布では2つのパラメータによって形が変わります。
そのため、以下2つのパラメータでそれぞれ偏微分して=0と置いた式、両方を満たすパラメータの最尤推定値を求めます。

\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{dL(\mu, \sigma^{2})}{d\mu} = 0 ・・・① \\
& \frac{dL(\mu, \sigma^{2})}{d\sigma^{2}} = 0 ・・・②
\end{aligned}
\right.
\end{equation}

 

対数尤度関数に対して偏微分を行う

期待値パラメータで偏微分を行う

まず\(①\)の計算を行います。
第1項に\(\mu\)が入っていないので消えて、第2項に対して微分して、そして
\begin{eqnarray}
-2*\frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\hat{\mu_{}})^{2}}{2\sigma^{2}} &=& 0 \\
\sum_{k=1}^{n}(x_{k}-\hat{\mu_{}}) &=& 0 (\sigma^{2}が0より大きいので、分母を払う) \\
(x_{1}-\hat{\mu_{}})+(x_{2}-\hat{\mu_{}})+ ... + (x_{n}-\hat{\mu_{}}) &=& 0 \\
-n\hat{\mu_{}} &=& -\sum_{k=1}^{n}x_{k} \\
\hat{\mu_{}} &=& \frac{1}{n}\displaystyle \sum_{k=1}^{n}x_{k} \\
\hat{\mu_{}} &=& \bar{x}
\end{eqnarray}

 

分散パラメータで偏微分を行う

続いて、\(②\)の計算を行います。
\(\sigma^{2}\)で偏微分して、\(\displaystyle\frac{dL(\mu, \sigma^{2})}{d\sigma^{2}} = 0\)を計算します。
ここで注意はあくまで\(\sigma^{2}\)というパラメータに対して微分を行います。なので、\(\sigma^{2}\)を\(\sigma^{2}\)で微分すると1です。
わかりやすくするために、\(\sigma^{2}\)を\(\hat{\sigma_{}}\)として、計算をしていきます。
そのため、計算する方程式は、\(\displaystyle\frac{dL(\mu, \hat{\sigma_{}})}{d\hat{\sigma_{}}} = 0\)を計算します。
\(\hat{\sigma_{}}\)は0より大きいので、分母を払って、計算すると
以下が偏微分する対数尤度になります。
\begin{eqnarray}
L(\mu, \hat{\sigma_{}}) &=& -\frac{n}{2}{log(2\pi\hat{\sigma_{}})} + \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\hat{\sigma_{}}}
\end{eqnarray}

 

\begin{eqnarray}
-\frac{n}{2} \cdot \frac{1}{2\pi\hat{\sigma_{}}} \cdot {2\pi} + \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\hat{\sigma_{}}^{2}} &=& 0 \\
-\frac{n}{2} \cdot \frac{1}{\hat{\sigma_{}}} + \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{2\hat{\sigma_{}}^{2}} &=& 0 \\
- n\hat{\sigma_{}} + {\sum_{k=1}^{n}(x_{k}-\mu)^{2}} &=& 0 \\
\hat{\sigma_{}} &=& \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{n}
\end{eqnarray}

従って、上の計算処理は、ハットをつけていたので、元に戻して、
\begin{eqnarray}
\hat{\sigma^{2}_{}} &=& \frac{\displaystyle \sum_{k=1}^{n}(x_{k}-\mu)^{2}}{n}
\end{eqnarray}
が分散の最尤推定量となります。

 

以上のことから、正規分布の最尤推定量は、
\begin{eqnarray}
\hat{\mu_{}} &=& \bar{x} \\
\hat{\sigma^{2}_{}} &=& \frac{ \displaystyle \sum_{k=1}^{n}(x_{k}-\hat{\mu_{}})^{2}}{n}
\end{eqnarray}