正規分布に従うけど、
ある値以降のもののみをピックアップして、そのデータだけを用いて新しい分布を構築したい場合があるとする。
これを切断正規分布と言います。
例えばですが、人の資産の分布を考えると、プラスは預金などで持ってることになりますが、マイナスもありえます。
マイナスの場合は借金ということになります。
ただ、データとしてはプラスを考えたいし、プラスとした時の分布を見たい場合、マイナスのデータを考えずにプラスのデータだけで分布を作る必要があります。
このように、ある条件を区切ってその部分だけで分布を構築する手法です。
逆ミルズ比
\begin{eqnarray}
f(x|x > c)
&=& \displaystyle \frac{f(x, x > c)}{\displaystyle \int_{c}^{\infty}f(x)dx} \\
&=& \displaystyle \frac{f(x)}{\displaystyle \int_{c}^{\infty}f(x)dx} \\
&=& \displaystyle \frac{f(x)}{1-F(c)} \\
\end{eqnarray}
ここで、\(x \sim N(\mu, \sigma^{2})\)であることから、
現在の\(c\)地点は\(z\)軸\( \Big( = \displaystyle \frac{x-\mu}{\sigma} \Big) \)で変換した際の値は、\( \displaystyle \frac{c-\mu}{\sigma} \)になるので、
\begin{eqnarray}
p(x)
&=& f(x|x > c) \\
&=& \displaystyle \frac{f(x)}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \\
\end{eqnarray}
となります。
この状態で、\(x\)の期待値を求めてみると、
\begin{eqnarray}
E_{f}[x|x>c]
&=& \int_{c}^{\infty}xf(x|x>c)dx \\
&=& \int_{c}^{\infty}xp(x)dx \\
&=& \displaystyle \int_{c}^{\infty} \frac{xf(x)}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) }dx \\
&=& \displaystyle \frac{1}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \int_{c}^{\infty} x\frac{1}{\sqrt{2\pi}\sigma} \exp\Big\{\displaystyle -\frac{(x-\mu)^{2}}{2\sigma^{2}} \Big\} dx \\
&=& \displaystyle \frac{1}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \int_{c}^{\infty} x\frac{1}{\sqrt{2\pi}\sigma} \exp\Big\{\displaystyle -\frac{1}{2}\Big(\frac{x-\mu}{\sigma}\Big)^{2} \Big\} dx \\
\end{eqnarray}
ここで、\(\displaystyle t = \frac{x-\mu}{\sigma}\)とすると、\(dt = \displaystyle \frac{1}{\sigma}dx\)となり、そして\(\mu + t\sigma = x\)であることから、
\begin{eqnarray}
E[x]
&=& \displaystyle \frac{1}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \int_{\frac{c-\mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}}(\mu+t\sigma) \exp\Big( \displaystyle -\frac{t^{2}}{2}\Big) dt \\
&=& \displaystyle \frac{1}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \Big\{ \mu\Big(\int_{\frac{c-\mu}{\sigma}}^{\infty} \frac{1}{\sqrt{2\pi}}\exp\Big(-\frac{t^{2}}{2}\Big)dt\Big) + \sigma\Big( \int_{\frac{c-\mu}{\sigma}}^{\infty} t\frac{1}{\sqrt{2\pi}}\exp\Big(-\frac{t^{2}}{2}\Big)dt \Big) \Big\} \\
&=& \displaystyle \frac{1}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \Big\{ \mu\Big( 1-\Phi\Big(\frac{c-\mu}{\sigma}\Big) \Big) + \sigma\Big( \int_{\frac{c-\mu}{\sigma}}^{\infty} t\frac{1}{\sqrt{2\pi}}\exp\Big(-\frac{t^{2}}{2}\Big)dt \Big) \Big\} \\
\end{eqnarray}
この2行目の第1項目は\(N(0,1)\)の標準正規分布であることから、3行目の第1項に変換しています。
ここで、上の3行目の第2項について、
\(\displaystyle - \frac{1}{2}t^{2} = s\)とすると、\(-tdt = ds\)であることから、
第2項だけについて、
\begin{eqnarray}
第2項
&=& \int_{\frac{c-\mu}{\sigma}}^{\infty} t\frac{1}{\sqrt{2\pi}}\exp\Big(-\frac{t^{2}}{2}\Big)dt \\
&=& - \int_{-\infty}^{-\frac{1}{2}(\frac{c-\mu}{\sigma})^{2}} -\frac{1}{\sqrt{2\pi}}\exp(s)ds \\
&=& \frac{1}{\sqrt{2\pi}} \Big[ \exp(s) \Big]_{-\infty}^{-\frac{1}{2}(\frac{c-\mu}{\sigma})^{2}} \\
&=& \frac{1}{\sqrt{2\pi}} \Big\{ \exp\Big(-\frac{1}{2}\Big(\frac{c-\mu}{\sigma}\Big)^{2}\Big) - \exp(-\infty) \Big\} \\
&=& \frac{1}{\sqrt{2\pi}} \Big\{ \exp\Big(-\frac{1}{2}\Big(\frac{c-\mu}{\sigma}\Big)^{2}\Big) \Big\} \\
\end{eqnarray}
第2項は、\(\exp(-\infty) \rightarrow 0\)となるので0となる。
そして上は、まさに\(N(0,1)\)の標準正規分布となるので、第2項は、
\begin{eqnarray}
第2項
&=& \phi\Big(\frac{c-\mu}{\sigma}\Big) \\
\end{eqnarray}
となる。
以上のことから、
\begin{eqnarray}
E[x]
&=& \displaystyle \frac{1}{ 1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big) } \Big\{ \mu\Big( 1-\Phi\Big(\frac{c-\mu}{\sigma}\Big) \Big) + \sigma\phi\Big(\frac{c-\mu}{\sigma}\Big) \Big\} \\
&=& \mu + \sigma\frac{\phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big)}{1-\Phi\Big(\displaystyle \frac{c-\mu}{\sigma}\Big)} \\
\end{eqnarray}
この\(E[x]\)は\(p(x)\)で計算してるので、厳密には\(E[x|x>c]\)であることに注意。
これは何に使えるのか?
これは、EMアルゴリズムなど、欠損値があった際に期待値で欠損値に値を埋め込むみたいなことをしたりします。
よくその欠損のある説明変数の平均値をとってそれを入れる手法であったり、すでにあるデータから回帰分析で予測してその値を入れる手法であったりと、欠損データに対してどういう値を入れて完全データにするのが良いのかが議論されます。
その中の1つとして、上記のように条件付き期待値を取ってその値を埋め込む手法が上で説明したミルズ比になったりします。
トービットモデル
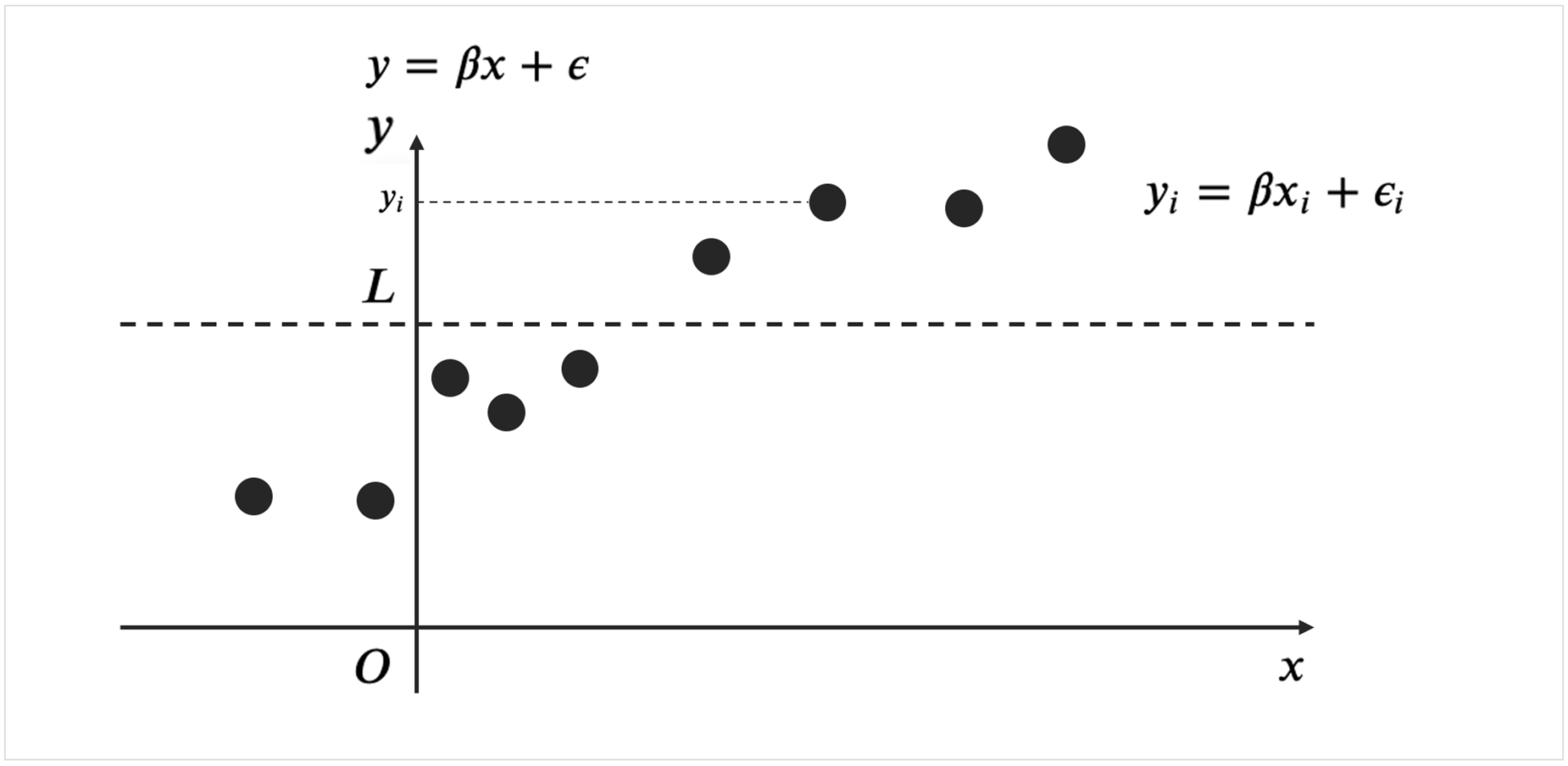
トービットモデルとは、目的変数が限られた範囲の値しかとらない場合があるときに構築する回帰モデルのことです。
例えば資産のデータを考える際、この資産を予測する場合があるとする。
資産をマイナスを取らない場合を想定すれば、説明変数を\(x\)とした時、回帰モデルは、
\(y_{i} = \beta x_{i} + \epsilon_{i}\)となります。
ここで、\(\epsilon \sim N(0,\sigma^{2}) \)とします。
そうすると、\(\epsilon_{i} = y_{i} - \beta x_{i} \)となることと、
\(\epsilon \sim N(0,\sigma^{2}) \)に従うことから、\(\epsilon\)は正規分布に従うので、
まず\(y_{i}\)について、尤度関数を求めると、
\begin{eqnarray}
L(\beta, \sigma)
&=& f(y_{1}) * f(y_{2}) \cdot \cdot \cdot f(y_{n}) \\
\end{eqnarray}
ここで、イプシロンの式に変形する。
ここで、一般的に標準正規分布と標準分布は以下のように表記される。
\begin{eqnarray}
\phi(x)
&=& \frac{1}{\sqrt{2\pi}} \exp\Bigr(-\frac{x^{2}}{2}\Bigr) \\
\end{eqnarray}
【標準分布】
\begin{eqnarray}
\Phi(x)
&=& \int_{-\infty}^{x} \phi(t)dt \\
\end{eqnarray}
ここで、\(\epsilon \sim N(0,\sigma^{2}) \)であることから、
\begin{eqnarray}
f(\epsilon)
&=& \frac{1}{\sqrt{2\pi}} \exp\Bigr(-\frac{\epsilon^{2}}{2}\Bigr) \\
\end{eqnarray}
ここで、\(y_{i} = \beta x_{i} + \epsilon_{i}\)により、\(\epsilon_{i} = y_{i} - \beta x_{i}\)であるため、\(d\epsilon = dy\)。
そして、
\begin{eqnarray}
Z
&=& \frac{\epsilon_{i} - E[\epsilon_{i}]}{\sqrt{V(\epsilon_{i})}} \\
&=& \frac{y_{i} - \beta x_{i} - 0}{\sqrt{\sigma^{2}}} \\
&=& \frac{y_{i} - \beta x_{i}}{\sigma} \\
\end{eqnarray}
そして、これに対して、両辺をZで微分すると、
\begin{eqnarray}
dZ
&=& \frac{1}{\sigma}dy
\end{eqnarray}
となるので、
\begin{eqnarray}
f(y)
&=& \frac{1}{\sigma}\phi\Bigr(\frac{y_{i} - \beta x_{i}}{\sigma}\Bigr)
\end{eqnarray}
となる。これは\(y_{i}\)が\(L\)以上の時を想定。
逆に、\(y_{i}\)が\(L\)未満の時は、一律確率は、\(1-\Phi\Bigr(\displaystyle \frac{x_{i}\beta - L}{\sigma} \Bigr) \)なので、
尤度関数は、
\begin{eqnarray}
L(\beta, \sigma)
&=& \prod_{i=1}^{n} \Bigr[ \frac{1}{\sigma}\phi\Bigr(\frac{y_{i} - \beta x_{i}}{\sigma}\Bigr) \Bigr]^{I(y_{i})} \prod_{l=1}^{m} \Bigr[ \Phi\Bigr(\displaystyle \frac{x_{i}\beta - L}{\sigma} \Bigr) \Bigr]^{I(y_{l})}
\end{eqnarray}
\begin{eqnarray}
L(\beta, \sigma)
&=& f(y_{1}) * f(y_{2}) \cdot \cdot \cdot f(y_{n}) \\
\end{eqnarray}
\(y_{i}\)に0か1が割り振られ、そしてそれに対して、確率密度関数が割り当てられる。