
棄却サンプリング
ここでは棄却サンプリングについて説明しますが、
マルコフ積分と呼ばれる解析的に計算をすることのできない積分をサンプリングを用いて推定するという仕組みを提供します。
pythonや統計解析ソフトRなどでは正規分布などよくある基本的な関数からのサンプリングはできますが、
不明な関数からのサンプリングはできない場合に、どのようにしてサンプリングを行うかが争点となります。
棄却サンプリングとは,サンプルを生成したい分布を覆うようなよく知られた分布から生成したサンプルを用いて,サンプリングを行う方法です.
予測分布\(p(z)\)のサンプルを提案分布\(q(z)\)から求めることを考えます.
このとき\(p(z) < kq(z)\)が満たされているものとします
→ つまり、\(p(z) < kq(z)\)なので、\(kq(z)\)でサンプリングしたい\(p(z)\)を覆い尽くすようにする。
まさにこれって、モンテカルロ法の正方形で囲むものと同じ考え方です。
まず知っている\(q(z)\)からサンプリングをします。
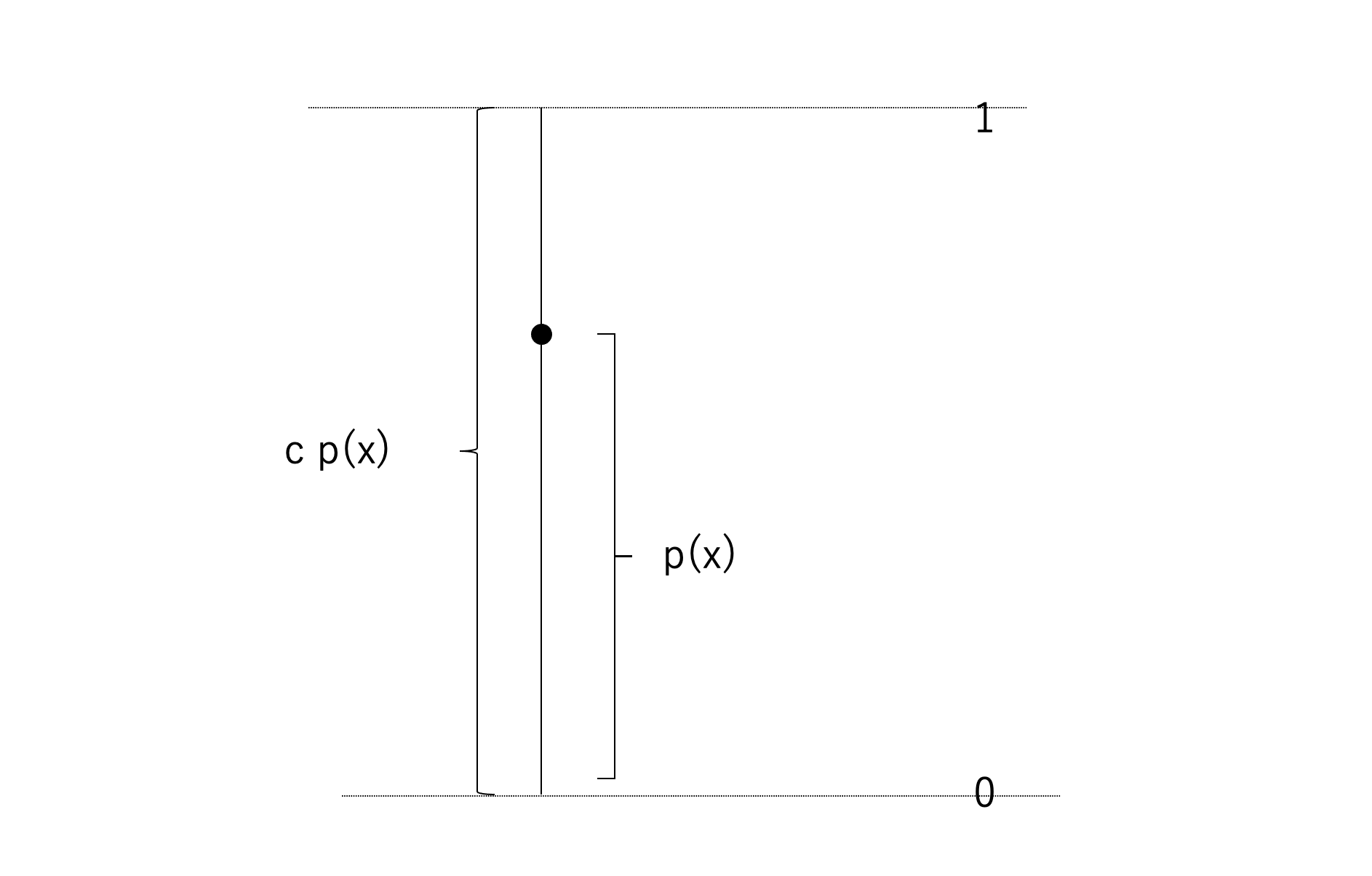
そして\(p(z)\)と\(q(z)\)の比率は0から1なので、その間に対応して、0から1でランダムな数値を出します。
そして\(q(z)\)からもデータのサンプリングをします。
この2つの結果を用いて以下の判定をします。
\(u < \displaystyle \frac{p(z)}{cq(z)}\)であれば、
ただ注意としては、なかなかこの\(p(z) < kq(z)\)を満たす、全ての\(z\)に対してこの式が成り立つような\(q(z)\)を満たす関数を出すのが難しい。
なので、この棄却サンプリングに加えてさらに条件をつけて、サンプリングをするような手法が次のやり方になります。
でも今回結果的には\(\displaystyle f \left(x | u < \frac{p(z)}{cq(z)} \right)\)からサンプリングして上記を満たすサンプリングをしたわけだが、本当にこれだけで\(p(z)\)からのサンプリングに帰着できるのでしょうか?
まずベイズの定理から以下のように変換することができます。\(\theta\)はパラメータ群を表しているとして、
\begin{eqnarray}
f(\theta|x)
&=& \displaystyle \frac{f(x,\theta)}{f(x)} \\
&=& \displaystyle \frac{f(x|\theta)f(\theta)}{f(x)} ・・・① \\
\end{eqnarray}
ここで\(f(x)=\displaystyle \int f(x|\theta)f(\theta)d\theta \)であることを利用して、
\begin{eqnarray}
f(\theta|x)
&=& ①\\
&=& \displaystyle \frac{f(x|\theta)f(\theta)}{\displaystyle \int f(x|\theta)f(\theta)d\theta }
\end{eqnarray}
となります。
これを利用して、以下のように変換できます。
実際には以下のように帰着でき、
\begin{eqnarray}
f\left(z|u < \displaystyle \frac{p(z)}{cq(z)} \right)
&=& \frac{P\left(u < \displaystyle \frac{p(z)}{cq(z)}|z\right)q(z)}{\displaystyle \int P\left(u < \displaystyle \frac{p(z)}{cq(z)}|z\right)q(z)dz} \\
&=& \frac{\displaystyle \{p(z)/cq(z)\}q(z) }{\displaystyle \int \{p(z)/cq(z)\}q(z)dz} \\
&=& \displaystyle \frac{ p(z) }{ \displaystyle \int p(z)dz} \\
&=& p(z)
\end{eqnarray}
上の式の意味としては、条件付き確率なので、
まずサンプリングをした上で、\(u\)より大きいかの確率を出してます。
その中で計算していくと、そのサンプリングは結果的には\(p(z)\)から出たものと同値なので、このサンプリング方法でうまくいくということになります。
ただ欠点としては、そういった\(q(z)\)を求めることが難しいです。
もし\(q(z)\)を大きく作るのでも良さげ!って思いますが、その場合、各\(z\)ごとの\(p(z)\)と\(q(z)\)の比率がめちゃくちゃ小さくなるので、
0から1のサンプリングをするとき、受容するデータが極端に少なくなり、そうなると処理が長時間に及ぶ可能性があるためです。
これもある確率密度関数の下の面積を求めるので、
モンテカルロ法の原理のように、ある区間で正方形や長方形などを立てて、その中にランダムにサンプリングをします。
それに対して、確率密度関数の下の部分を赤く塗って、上を青く塗って処理をすれば、同じように赤点と青点の比率を求めることで、面積を求めることができます。
ただどのくらい正方形を立てれば良いか予測が難しいと言うこと、大きく正方形をとってもサンプリングに時間がかかるので難しくなります。
そのためx=x_{1}において、確率密度関数のk倍にして、考えることでこのk倍した関数をいわゆる正方形や長方形みたいなことにします。