統計学を学びたいけど、やたら数式ばっかでわからない!!
計算どうやってるのか全然わからない!
ベクトルや行列、微分がよくわからず、勉強挫折してしまう、、
など統計学はとにかく数式が多いです。
統計ってちょっと平均値や中央値など一般的な指標を扱うくらいであれば全然必要ないですが、より深い統計学を学ぼうとすると、数学を学んでいないと理解することすらできません。
なので、今回はそんな統計学を学んでいく上で、最低限これを知っていれば統計学の門を叩くことできるよ!というのを紹介してみようと思います!
初めての人は心して読んでいただき、すでに知ってるよーって方は復習がてら読んでもらえるとありがたいです!
Contents
ベクトルと行列
ベクトルの計算と内積
(どこでも)
→ ベクトルの内積は頻繁に出てくるので注意。
さらにベクトルの掛け方によって、結果がスカラー値(定数)になるか、行列になるか変わるので要注意。
そして行列の計算を行うときは、上の計算がベースとなります。
\begin{eqnarray}
(a, b)
\begin{pmatrix}
c \\
d \\
\end{pmatrix}
&=& ac+bd \\
\begin{pmatrix}
a \\
b \\
\end{pmatrix}
(c, d)
&=&
(ac, bd)
\end{eqnarray}
になります。
行列の計算
\begin{eqnarray}
\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}
\begin{pmatrix}
a' & b' \\
c' & d' \\
\end{pmatrix}
&=&
\begin{pmatrix}
aa'+bc' & ab'+bd' \\
ca'+dc' & cb'+dd' \\
\end{pmatrix}
\end{eqnarray}

大事な考えとして、行列の各要素はベクトルになっているということです。これを知っておけば、計算も分解して考えられるようになります。
行列式の計算(2次元正方行列)
表記としては、\(A\)の行列式は\(|A|\)や\(det(A)\)と表記します。
主に、多変量正規分布を求める際に出てきたりします。
\begin{eqnarray}
|A| = det(A) = ad-bc \\
\end{eqnarray}
逆行列について
逆行列を計算するのは多変量正規分布や、この後扱う正規方程式などで使用したりします。
\begin{eqnarray}
A^{-1}
&=& \frac{1}{|A|}
\begin{pmatrix}
d & -b \\
-c & a \\
\end{pmatrix}
\end{eqnarray}
\begin{eqnarray}
AA^{-1} = I ・・・① \\
AA^{T} = I ・・・②
\end{eqnarray}
などの正則行列(逆行列を持つ)、対象行列&転置行列による単位行列
などここをわかっておけば、正規分布や最小二乗法のベクトル・行列計算ができるようになります。
行列の種類
→ 正方行列、正則行列、対称行列、転置行列、単位行列の5つ。これらの性質を理解する。
正方行列:n次元(n×n)行列のこと。
単位行列:n次元(n×n)行列で、(k,k)では全て値は1で、(k,l)(k≠l)では全て値が0となる行列のこと。正方行列と単位行列をかけると必ず同じ正方行列になります。
正則行列:AB=BA=Iを満たすBのこと?逆行列を持つ。これにより、正則行列と正則行列の逆行列は単位行列になります。
対称行列:列と行が対称になっている。
転置行列:これはどのものでも転置したら転置行列になります。正方行列でも正則行列でも対称行列でも。ただ1つ大事なのは、対称行列と転置した転置行列を掛け合わせると単位行列になります。これ大事です。
| 種類 | 説明 |
|---|---|
| 正方行列 | \(n\)次元(\(n\)×\(n\))行列のこと。 |
| 単位行列 | \(n\)次元(\(n\)×\(n\))行列で、(\(k\),\(k\))では全て値は1で、(\(k\),\(l\))(ただし\(k\)≠\(l\))では全て値が0となる行列のこと。正方行列と単位行列をかけると必ず同じ正方行列になります。 |
| 正則行列 | \(AB=BA=I\)を満たすBのこと?逆行列を持つ。これにより、正則行列と正則行列の逆行列は単位行列になります。 |
| 転置行列 | これはどのものでも転置したら転置行列になります。正方行列でも正則行列でも対称行列でも。ただ1つ大事なのは、対称行列と転置した転置行列を掛け合わせると単位行列になります。 |
| 対称行列 | 列と行が対称になっている。 |
単位行列
\begin{eqnarray}
I &=&
\begin{pmatrix}
1 & 0 \\
0 & 1 \\
\end{pmatrix}
\end{eqnarray}
(1,1)や(2,2)では1が、(1,2)や(2,1)では0の値が入ってます。
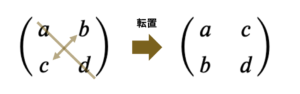
転置行列
\begin{eqnarray}
A &=&
\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix} \\
\end{eqnarray}
としたとき、\(A\)の転置行列である\(A^{T}\)は、
\begin{eqnarray}
A^{T} &=&
\begin{pmatrix}
a & c \\
b & d \\
\end{pmatrix} \\
\end{eqnarray}
となります。
以下のように、転置行列の(1,1)や(2,2)などの(k,k)に線を入れて、そこを軸として行と列を入れ替えたものになります。
今回は2次元正方行列を扱ってるので、(1,2)のものは(2,1)に、(2,1)のものは(1,2)に値が移動します。
対称行列
対称行列は(1,1)や(2,2)などの(k,k)を軸に、対称である行列のことです。
\begin{eqnarray}
A &=&
\begin{pmatrix}
a & b \\
b & d \\
\end{pmatrix} \\
\end{eqnarray}
のようなものです。
●行列の性質。
\((AB)^{T} = B^{T}A^{T}\)
転置させると並び順が逆になります。
よくある例で
対称行列の時、まずAA-1=Iは成立しないので、そのまま。ただ転置すると、BをA-1で置き換えると以下のようになります。
\((AA^{-1})^{T} = (A^{-1})^{T}A^{T}\)
そしてさらに大事なのは、
\begin{eqnarray}
AA^{-1} = I ・・・① \\
AA^{T} = I ・・・②
\end{eqnarray}
①と②を比較すると、左辺は\(A\)で一緒、右辺は\(I\)で一緒。よって、\(A^{-1}\)と\(A^{T}\)は一緒になります。
つまり、\(A^{-1} = A^{T}\)になります。
ここで、この等式の両辺に転置をとってみたいと思います。転置を取ると、
- 左辺:\((A^{-1})^{T}\)
- 右辺:\((A^{T})^{T} = A\)になります。これは転置をして、さらに転置するので元に戻ります。よってそのままになります。
よって、\((A^{-1})^{T} = A\)になります。
意外とこの式使うこと多いです!特に、最小二乗法での回帰係数を行列で求める時です。
ココがポイント
\begin{eqnarray}
(A^{-1})^{T} = A
\end{eqnarray}
ベクトルや行列の微分について
(主に使うところとしては、主成分分析や、回帰分析など)
行列の微分、これは簡単です。
そもそも行列は上でも話した通り、ベクトルの集合体でベク取りによって成り立っています。
なのでベクトルの微分ができれば行列の微分もすぐ理解できます。
\begin{eqnarray}
\frac{\partial}{\partial \beta} X\beta &=& X ・・・③\\
\frac{\partial}{\partial \beta} \beta^{T}X\beta &=& 2X\beta ・・・④\\
\end{eqnarray}
実際に上で学んだことを用いて計算をしてみる
今回例として出すのは回帰分析で回帰係数を出すための手法である最小二乗法にて出てくる正規方程式です。
回帰分析で
\begin{eqnarray}
y_{1} &=& \beta_{11}x_{11} + \epsilon_{1} \\
y_{2} &=& \beta_{21}x_{21} + \epsilon_{2} \\
y_{3} &=& \beta_{31}x_{31} + \epsilon_{3} \\
y_{n} &=& \beta_{n1}x_{n1} + \epsilon_{n} \\
\end{eqnarray}
とします。そうするとこれは、
\begin{eqnarray}
y &=& X\beta + \epsilon
\end{eqnarray}
となります。
上の式から、\(\epsilon = y - X\beta\)であることから、
最小二乗法\(\epsilon\epsilon^{T}\)により、
\begin{eqnarray}
\epsilon^{T}\epsilon
&=& (y - X\beta)^{T}(y - X\beta) \\
&=& (y^{T} - (X\beta)^{T})(y - X\beta) \\
&=& (y^{T} - \beta^{T}X^{T})(y - X\beta) \\
&=& y^{T}y - y^{T}X\beta - \beta^{T}X^{T}y + \beta^{T}X^{T}X\beta \\
\end{eqnarray}
この式に対して\(\beta\)で偏微分を実行します。
\begin{eqnarray}
\frac{\partial}{\partial \beta}\epsilon^{T}\epsilon
&=& \frac{\partial}{\partial \beta} \{ y^{T}y - y^{T}X\beta - \beta^{T}X^{T}y + \beta^{T}X^{T}X\beta \} \\
&=& \frac{\partial}{\partial \beta} y^{T}y - \frac{\partial}{\partial \beta} y^{T}X\beta - \frac{\partial}{\partial \beta} \beta^{T}X^{T}y + \frac{\partial}{\partial \beta} \beta^{T}X^{T}X\beta \\
\end{eqnarray}
\(y^{T}y\)に\(\beta\)がないので、\(\beta\)で微分すると定数となるため、
\begin{eqnarray}
\frac{\partial}{\partial \beta} y^{T}y &=& 0 \\
\end{eqnarray}
\(y^{T}X\)は計算すると行列になるので、偏微分の③が使用できるので、
\begin{eqnarray}
\frac{\partial}{\partial \beta} y^{T}X\beta &=& y^{T}X \\
\end{eqnarray}
\(X^{T}X\)は計算すると行列になるので、\(\beta^{T}\)行列\(\beta\)となるので、偏微分の④が使用できるので、
\begin{eqnarray}
\frac{\partial}{\partial \beta} \beta^{T}X^{T}X\beta &=& 2X\beta \\
\end{eqnarray}
●行列を含んだ方程式の計算
ポイントは右から
スカラー値であれば、特に数字を左からかけないといけないとか、右からかけないといけないとかそういったものは意識していませんでした。
ただこの行列の計算をする場合は、左からかけるのか、右からかけるのかを意識する必要があります。
理由としては上のベクトル計算で述べたとおり、
ベクトルの掛け方によって計算結果は変わること
行列はベクトルによってできていること
そのため、ベクトルの計算によって結果変わるのであれば、それを要素にもつ行列も掛け方によって計算結果が変わるのは想像できますよね。
なので、左から行列をかけるのか、右から行列をかけるのかが重要になります。
統計学を学んでいく際の線形代数学は、これだけを覚えておけばまず大丈夫です!
初学者にとってはかなり難易度の高く、内容も濃かったですが、1つ1つ噛み砕いて説明してみました。
もしわからないということがあれば、お気軽に右上のフォームから回答いたします!