回帰分析と分散分析の関係はとても近いです!
回帰分析ではあるデータ(目的変数)が取れて、それに対して別の変数(説明変数)でどのくらいの影響があるかを示すものです。
式で表すと、\(y = \beta x + \epsilon\)と表せます。
そして、これに対して、
分散分析でもあるデータが取れて、それに対して因子があり、その因子によってデータが生成されているものと想定します。
つまり、\(y = \mu + \alpha_{1} + \epsilon\)と表せます。
2つの式を見てもなんだか似てますよね!
これら2つは、
あるデータがあって、そのデータは何が要因となってそのデータ(値)が生成されているのか、そしてどんな影響によって説明される値なのか、
を分析するものです。
ここではそんな、回帰分析と分散分析の関係性について探っていこうと思います。
回帰分析での分散分析表
| 要因 | 式 | 自由度 | 説明 |
|---|---|---|---|
| 回帰変動 | \( \displaystyle \sum_{i=1}^{n} (\hat{y_{i}}-\bar{y})^{2} \) | \(p\) | 説明変数による数値の変動 → 説明変数によって説明ができる |
| 誤差変動 | \( \displaystyle \sum_{i=1}^{n} (y_{i} - \hat{y_{i}})^{2} \) | \(n-p-1\) | ホワイトノイズ(誤差)による数値の変動 |
| 全体変動 | \( \displaystyle \sum_{i=1}^{n} (y_{i}-\bar{y})^{2} \) | \(n\) | 平均値と取れたデータの変動 |
回帰変動はいわゆる、説明変数による要因を想定した変動です。
ここで回帰分析でのF検定をしてみます。そのためにはF検定統計量をまず導出します。
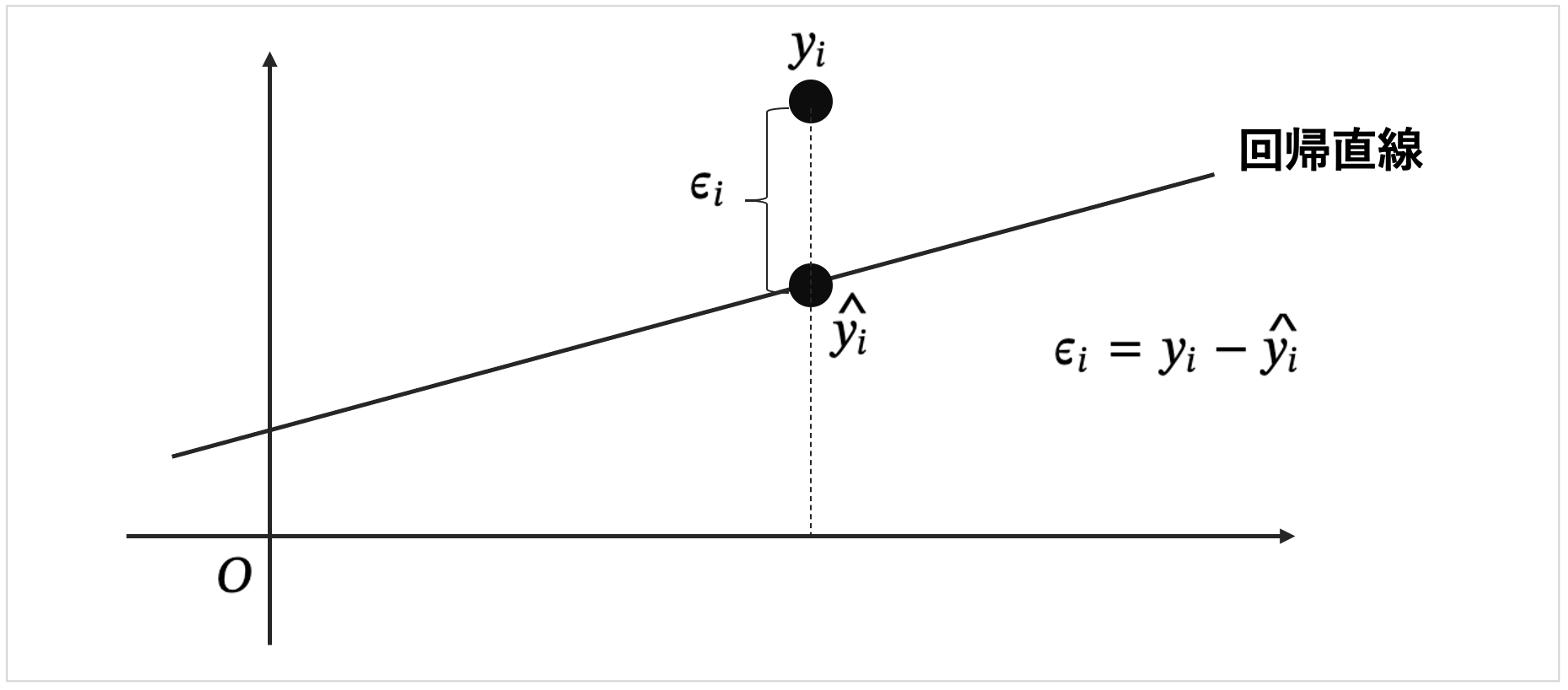
回帰分析の結果として、\(\epsilon_{i} = y_{i} - \hat{y_{i}} \)であるから、
\begin{eqnarray}
\epsilon_{i} &=& y_{i} - \hat{y_{i}} \\
y_{i} &=& \hat{y_{i}} + \epsilon_{i} \\
y_{i} - \bar{y} &=& (\hat{y_{i}} - \bar{y}) + \epsilon_{i} \\
(y_{i} - \bar{y})^{2} &=& \{(\hat{y_{i}} - \bar{y}) + \epsilon_{i}\}^{2} \\
(y_{i} - \bar{y})^{2} &=& (\hat{y_{i}} - \bar{y})^{2} + (\hat{y_{i}} - \bar{y})\epsilon_{i} + \epsilon_{i}^{2} \\
\sum_{i=1}^{n}(y_{i} - \bar{y})^{2} &=& \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2} + \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})\epsilon_{i} + \sum_{i=1}^{n}\epsilon_{i}^{2} ・・・① \\
\sum_{i=1}^{n}(y_{i} - \bar{y})^{2} &=& \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2} + \sum_{i=1}^{n}\epsilon_{i}^{2} \\
\sum_{i=1}^{n}(y_{i} - \bar{y})^{2} &=& \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2} + \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2} ・・・② \\
(全体変動 &=& 回帰変動 + 誤差変動) \\
(全体変動の自由度 &=& 回帰変動の自由度 + 誤差変動の自由度) \\
(n &=& (p-1) + (n-(p-1))) \\
\end{eqnarray}
と分解することができます。
ちなみにこの\(②\)式は重要で、決定係数やこの後扱うF検定統計量の考えがあったりします。
そして、①の部分ですが、右辺の第2項である、以下の部分が0になっています。
\begin{eqnarray}
\sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})\epsilon_{i} + \sum_{i=1}^{n}\epsilon_{i}^{2} &=& 0 \\
\end{eqnarray}
これの式の意味としては、「予測値とデータの平均値の差」と「残差」の相関は0ということを言っています。
決定係数
決定係数\(R^{2}\)は、どのくらい説明変数によって説明されているかなので、イメージ回帰変動/全体変動と想像できると思います。なので、回帰変動/全体変動を\(①\)から導出すると、
\(①\)に対して、\(\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}\)で割ると、
\begin{eqnarray}
1 &=& \frac{\displaystyle \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}} + \frac{\displaystyle \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}} \\
1 - \frac{\displaystyle \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}} &=& \frac{\displaystyle \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}} \\
\end{eqnarray}
となります。
右辺が決定係数\(R^{2}\)になり、決定係数は以下で表されます。
\begin{eqnarray}
R^{2} = \frac{\displaystyle \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}} = 1 - \frac{\displaystyle \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}}
\end{eqnarray}
このように2通りの表し方があることも覚えておくのが良いでしょう!
そして、なぜ決定係数って\(R\)なんでしょうか。
実は、決定係数は相関係数の2乗です。
つまり相関係数は一般的に\(R\)なので、決定係数は\(R^{2}\)となります。
ただし、回帰曲線ではなく回帰直線の場合に限ります。
F検定統計量
回帰分析でのF検定は、「各説明変数が0でないかどうか」を検定します。
つまり、回帰係数を\(\beta_{i}\)としたとき、
\(\beta_{1} = \beta_{2} = \cdot\cdot\cdot = \beta_{l} = 0\)
ではないか?ということです。
通常仮説検定では2つの群の平均値を検定します。3つ以上の群があった場合、2つの群を3つの組み合わせにしてそれぞれ検定してというやり方が思いつきそうですが、それではダメです。
群ではないが、今回のように複数の回帰係数(説明変数)を検定する場合はF検定でないといけません。
これが帰無仮説でこれを弾く必要があります。もしこれが採択されると、全て回帰係数が0つまり説明変数の影響は皆無で、得られた目的変数のデータは全てホワイトノイズによって生成されたものと判定されてしまいます。
F検定統計量\(F\)は、
\begin{eqnarray}
F &=& \frac{回帰変動}{誤差変動}
\end{eqnarray}
となるので、そのような形にするために、\(①\)を\(\displaystyle \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}\)で割ると、
\begin{eqnarray}
\frac{\displaystyle \sum_{i=1}^{n}(y_{i} - \bar{y})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}} &=& \frac{\displaystyle \sum_{i=1}^{n}(\hat{y_{i}} - \bar{y})^{2}}{\displaystyle \sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}} + 1 \\
\end{eqnarray}
誤差による変動に対して、回帰変動つまり説明変数によって説明できる部分が多ければ回帰分析としては良いので、上記検定統計量を考えたときに値が大きければ良い。(誤差に対して回帰の比率が大きいほどよい)
分散分析での分散分析表
| 要因 | 式 | 自由度 | 説明 |
|---|---|---|---|
| 因子\(A\)(\(S_{A}\)) | \( \displaystyle \sum_{i=1}^{a} \sum_{j=1}^{n} (\bar{y_{A_{i}}}-\bar{y})^{2}= n\sum_{i=1}^{a}(\bar{y_{A_{j}}}-\bar{y})^{2} \) | \(a-1\) | 因子\(A\)による数値の変動 → 説明変数によって説明ができる |
| 誤差変動(\(S_{E}\)) | \( \displaystyle \sum_{i=1}^{a} \sum_{j=1}^{n} (\bar{y_{ij}}-\bar{y_{A_{i}}})^{2} \) | \(an-1-(a-1) = a(n-1) \) | ホワイトノイズ(誤差)による数値の変動 |
| 全体変動(\(S_{T}\)) | \( \displaystyle \sum_{i=1}^{a} \sum_{j=1}^{n} (y_{ij}-\bar{y})^{2} \) | \(an-1\) | 平均値と取れたデータの変動 |
因子\(A\)は、因子\(A\)による要因を想定した変動です。
1つ目の因子の自由度では、平均値と各水準の平均値を使って計算しています。
平均値は固定であるとすると、水準は今a個あり、1つずつ計算に使っていくと最終的に1つは固定で平均値が決まります。
なので、自由度はa-1個となります。
全体変動も同様で、各n個のデータと、平均値があり、平均値はこのn個のデータを用いて算出された値になります。
n-1個までは自由に値を取れるけど、平均値が定まっている以上、最後の1つのデータは自由な値を取ることはできず、計算から決まります。
なので、全体変動では自由度はn-1個となります。
最後に、誤差変動の自由度については、
全体変動 = 因子変動 + 誤差変動ということからも、
全体変動の自由度 = 因子変動の自由度 + 誤差変動の自由度から、
誤差変動の自由度 = 全体変動の自由度 - 因子変動の自由度 = n-1 - (a-1) = n-aとなります。
F検定統計量
分散分析でのF検定は、「因子の各水準が0でないかどうか」を検定します。
つまり、係数を\(\alpha_{i}\)としたとき、
\(\alpha_{1} = \alpha_{2} = \cdot\cdot\cdot = \alpha_{l} = 0\)
ではないか?ということです。
これが帰無仮説でこれを弾く必要があります。もしこれが採択されると、全て回帰係数が0つまり説明変数の影響は皆無で、得られた目的変数のデータは全てホワイトノイズによって生成されたものと判定されてしまいます。
全くもって、回帰分析でのF検定と同じですね!
回帰分析と同様に、分散分析もF検定を考えることができ、F検定統計量は\(F = \frac{回帰変動}{誤差変動}\)になります。
そして、誤差は回帰分析、分散分析ともに、\(N(0,\sigma^{2}\)を仮定してます。
ココがポイント
回帰分析、分散分析ともに、得られたデータがホワイトノイズによってではなく、どのくらい説明変数・因子によって説明されたかをF検定によって分析する。
そしてそのF検定統計量はともに、
\begin{eqnarray}
F &=& \frac{回帰変動/自由度}{誤差変動/自由度}
\end{eqnarray}
回帰分析と分散分析では両方ともF検定というものがありました。
それぞれのF検定での帰無仮説を見てみると、
回帰分析では、回帰係数を\(\beta_{i}\)としたとき、
\(H_{0} : \beta_{1} = \beta_{1} = \beta_{2} = \cdot\cdot\cdot = \beta_{k} = 0\)であり、
分散分析では、各水準の平均値を\(\mu_{i}\)としたとき、
\(H_{0} : \mu_{1} = \mu_{1} = \mu_{2} = \cdot\cdot\cdot = \mu_{l} = 0\)であり、
それぞれ説明変数や平均値が全て0であるということを検定している。
分散分析での変動値は因子の各水準のことで、
回帰分析での変動値は説明変数のことです。
回帰分析では、説明変数の影響度合いを重み付けした説明変数の和に、ノイズを加味したデータを表し、
分散分析では、各水準の平均的な値にノイズを加味したデータを表す。
このように、取れたデータに対してそれぞれ変動するものがあり、