分散分析とは、3つ以上のグループ間に有意差があるかないかを分析するための手法になります。
普通の検定では帰無仮説を基準にして対立仮説がこのくらい離れると有意性であったり、2つの群の差を見て有意性あるかなどの判断をします。帰無仮説も1つの群と見做せば、結局2つのグループ間を分析しているに過ぎません。
しかし3つ以上となると通常の検定の方法は使用できなくなります。
そこで考える手法として今回扱う分散分析というものがあります。分散分析は手法の名前で、このような3つ以上のグループ間の分析をするのが多重比較といったりします。
そして分散分析と言ってるので、主に分散を用いた分析手法になります。
Contents
分散分析のパターン
分散分析にはいくつかの種類があります。
・「一元配置分散分析」:1つの因子からなるデータを分析する方法で、因子に含まれる水準間の平均値の差を見ることができます。例えば、ある学校の1組、2組、3組の算数のテストのデータがある場合、一元配置分散分析を用いて、1組、2組、3組の算数のテストの平均点に差があるかどうかを検定できます。
→ A + ε
・「二元配置分散分析」:2つの因子からなるデータを分析する方法で、各因子における水準間の平均値の差を見ることができます。また、2つの要因が組み合わさることで現れる相乗効果の有無の確認もできます。例えば、薬A、B、Cをそれぞれ10mg、20mg投与した場合の効果についてのデータがある場合、二元配置分散分析を用いて薬の種類によって得られる平均値に差があるか、あるいは薬の投与量によって得られる平均値に差があるかどうかを検定できます。
→ 2つの因子を分析するので、その2つの因子が絡み合った場合も考える必要がある。
→ A + B + AB + ε
分散分析
分散分析は3つのグループ間の平均値に差がないかを検証する方法。
なので、A、B、Cグループがあったとして、
以下3つの組み合わせでそれぞれ検定をすれば良いかと思います。
A-B
B-C
C-A
しかしこの検定をすると、それぞれの有意水準を0.05とした時、
これらが同時になると考えると互いに排反だと仮定したとき、
(1-0.05)^3 = 84%になり、第1種の錯誤(有意水準)が想定よりも16%も大きくなってしまいます。
1元配置分散分析
1元配置分散分析は、1つのカテゴリで複数の水準間を判定する場合に使います。
例としては、
国ごとの身長のデータがあった時、

1つの要因で、複数の水準間での差を検定します。
上では1つの要因が身長で、水準が各国ということになります。
以下に図を置く。
分散分析の検定統計量となるFは、
\begin{eqnarray}
F &=& \frac{層間分散(S_{B})}{層内分散(S_{W})}
\end{eqnarray}
総平方和と層内分散と層間分散
全体の分散は、
全てのデータ\(y_{ij}\)と、全てのデータでの平均値を\(\bar{y}\)とすると、
総平方和\(S_{T}\)は、データ→そのグループでの平均→全平均なので、+と-でうまく入れて、
各データの代表値はそのグループの平均値になる。
そして全体を見た時の代表値は、各グループの平均値の平均値になる。
つまり2段階ある。
① グループの各データ(\(y_{ij}\)) → ② 各グループの平均値(\(\bar{y_{i}}\)) → ③ 全体の平均値(\(\bar{y_{}}\))
①と②が郡内の差分
②と③が群間の差分
と考えると、②が真ん中なので、②をプラスとマイナスで間に入れれば、それぞれの式が期待値になるのが想像できる。
①の平均値が②になるので、①を確率変数とした時、①の期待値は②になる。
②の平均値が③になるので、②を確率変数とした時、②の期待値は③になる。
(もちろん最初は①の全ての平均は③になることを利用して計算している。)
そして、
\begin{eqnarray}
S_{T}
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y})^{2} \\
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} \{y_{ij} - \bar{y_{i}} + \bar{y_{i}}- \bar{y} \}^{2} \\
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} \{(y_{ij} - \bar{y_{i}}) + (\bar{y_{i}}- \bar{y}) \}^{2} \\
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} \{(y_{ij} - \bar{y_{i}})^{2} + 2(y_{ij} - \bar{y_{i}})(\bar{y_{i}}- \bar{y}) + (\bar{y_{i}}- \bar{y})^{2} \} \\
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y_{i}})^{2} + \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} 2(y_{ij} - \bar{y_{i}})(\bar{y_{i}}- \bar{y}) + \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (\bar{y_{i}}- \bar{y})^{2} ・・・①\\
\end{eqnarray}
\(S_{T}\)は全てのデータ\(y_{ij}\)とその平均値である\(\bar{y_{}}\)を引いて2乗の和で計算しているので、まさに分散を表している。
▼ \(①\)の第1項目
\(①\)の第1項目は、単純な各グループごとの分散の和になります。
\(y_{ij}\)は各データ、そして\(\bar{y_{i}}\)はそのグループに対しての平均になり、それを和で表しているので、層内分散\(S_{W}\)になります。
\begin{eqnarray}
\sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y_{i}})^{2}
&=& \sum_{j=1}^{n_{1}}(y_{1j} - \bar{y_{1}})^{2} + \sum_{j=1}^{n_{2}}(y_{2j} - \bar{y_{2}})^{2} + ・・・ + \sum_{j=1}^{n_{n}}(y_{nj} - \bar{y_{n}})^{2} \\
&=& 水準1内の分散 + 水準2内の分散 + ・・・ + 水準n内の分散
\end{eqnarray}
▼ \(①\)の第2項目
\(①\)の第2項目は0になります。
▼ \(①\)の第3項目
\(①\)の第3項目は、分散の式と見比べて、各水準の平均が確率変数となり、それらの平均(=全平均)を引いているので、これは層間分散\(S_{B}\)になります。
iではなく、先にjで展開すると、サーメーション内の2乗の式にjがないので、
\begin{eqnarray}
\sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (\bar{y_{i}}- \bar{y})^{2}
&=& \sum_{i=1}^{n} n_{i}(\bar{y_{i}}- \bar{y})^{2}
\end{eqnarray}
よって、\(①\)の続きは、
\begin{eqnarray}
S_{T}
&=& ① \\
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y_{i}})^{2} + \sum_{i=1}^{n} n_{i}(\bar{y_{i}}- \bar{y})^{2} \\
&=& S_{W} + S_{B}
\end{eqnarray}
総変動 &=& 要因による変動 + 誤差による変動 \\
\sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y})^{2} &=& \sum_{i=1}^{n} n_{i}(\bar{y_{i}}- \bar{y})^{2} + \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y_{i}})^{2}
\end{eqnarray}
それぞれの意味を考えてみます。
| 項目 | 計算式 | 説明 |
|---|---|---|
| 総変動 | \( \displaystyle \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y})^{2}\) | (総平均と各データとの差分)\(^{2}\)の合計 |
| 要因変動 | \( \displaystyle \sum_{i=1}^{n} n_{i}(\bar{y_{i}}- \bar{y})^{2}\) | (各データとそのデータがある水準の平均との差分)\(^{2}\)の合計。つまり 水準Aの数(水準Aの平均-総平均)\(^{2}\) + 水準Bの数(水準Bの平均-総平均)\(^{2}\) |
| 誤差変動 | \( \displaystyle \sum_{i=1}^{n} \sum_{j=1}^{n_{i}} (y_{ij} - \bar{y_{i}})^{2}\) | (各データと、そのデータの水準の平均との差分)\(^{2}\)の合計 |
具体的に計算をしてみます
以下のようなデータを考えてみます!
| 要因 | データ | 平均 |
|---|---|---|
| 水準1 | 54, 35, 48, 56, 40, 45, 49, 36, 26 | 43.22 |
| 水準2 | 49, 40, 61, 66, 49, 59, 52 | 53.71 |
| 水準3 | 53, 45, 47, 54, 38, 41, 51 | 47.00 |
| 水準4 | 53, 59, 64, 37, 67, 25, 58, 50 | 51.63 |
| 総平均 | - | 48.61 |
上記のように1つの要因、つまり1元分散分析を考えてみます。水準は4つあります。
要因変動と、誤差変動を求めてみましょう!
要因変動\(S_{B}\)
全てのデータをそのデータのある水準の平均に置き換えてみます。
| 要因 | データ | 平均 |
|---|---|---|
| 水準1 | 43.22, 43.22, 43.22, 43.22, 43.22, 43.22, 43.22, 43.22, 43.22 | 43.22 |
| 水準2 | 53.71, 53.71, 53.71, 53.71, 53.71, 53.71, 53.71 | 53.71 |
| 水準3 | 47.00, 47.00, 47.00, 47.00, 47.00, 47.00, 47.00 | 47.00 |
| 水準4 | 51.63, 51.63, 51.63, 51.63, 51.63, 51.63, 51.63, 51.63 | 51.63 |
| 総平均 | - | 48.61 |
それぞれのデータと総平均を引いた値の2乗の合計を求めます!
水準1のデータ、40.33について、(40.33-47.77)\(^{2}\)を1つずつ計算して合計したものが、要因変動です。
つまり、水準1では40.33が9つ、水準2では7つ、水準3は7つ、水準4は8つなので、
\begin{eqnarray}
\begin{split}
S_{B}
&= \quad 9(43.22-48.61)^{2} \\
&\quad+ 7(53.71-48.61)^{2} \\
&\quad+ 7(47.00-48.61)^{2} \\
&\quad+ 8(51.63-48.61)^{2} \\
&= 534.6468
\end{split}
\end{eqnarray}
となります。
自由度は、水準が4つなので、4-1=3です。
誤差変動\(S_{w}\)
誤差変動は、
各水準の平均とそのデータの差分の2乗の合計になります。
| 要因 | データ | 平均 |
|---|---|---|
| 水準1 | 54, 35, 48, 56, 40, 45, 49, 36, 26 | 43.22 |
| 水準2 | 49, 40, 61, 66, 49, 59, 52 | 53.71 |
| 水準3 | 53, 45, 47, 54, 38, 41, 51 | 47.00 |
| 水準4 | 53, 59, 64, 37, 67, 25, 58, 50 | 51.63 |
水準1にはデータ54があり、水準1の平均は40.33なので、その差分の2乗なので、(54-40.33)\(^{2}\)
これを全てのデータで計算して合計します。
\begin{eqnarray}
\begin{split}
S_{W}
&= \quad (54-43.22)^{2} \\
&\quad+ (35-43.22)^{2} \\
&\quad+ (48-43.22)^{2} \\
&\quad+ (56-43.22)^{2} \\
&\quad+ (40-43.22)^{2} \\
&\quad+ (45-43.22)^{2} \\
&\quad+ (49-43.22)^{2} \\
&\quad+ (36-43.22)^{2} \\
&\quad+ (26-43.22)^{2} \\
&\quad+ (49-53.71)^{2} \\
&\quad+ (40-53.71)^{2} \\
&\quad+ (61-53.71)^{2} \\
&\quad+ (66-53.71)^{2} \\
&\quad+ (49-53.71)^{2} \\
&\quad+ (59-53.71)^{2} \\
&\quad+ (52-53.71)^{2} \\
&\quad+ (53-47.00)^{2} \\
&\quad+ (45-47.00)^{2} \\
&\quad+ (47-47.00)^{2} \\
&\quad+ (54-47.00)^{2} \\
&\quad+ (38-47.00)^{2} \\
&\quad+ (41-47.00)^{2} \\
&\quad+ (51-47.00)^{2} \\
&\quad+ (53-51.63)^{2} \\
&\quad+ (59-51.63)^{2} \\
&\quad+ (64-51.63)^{2} \\
&\quad+ (37-51.63)^{2} \\
&\quad+ (67-51.63)^{2} \\
&\quad+ (25-51.63)^{2} \\
&\quad+ (58-51.63)^{2} \\
&\quad+ (50-51.63)^{2} \\
&= 2866.85
\end{split}
\end{eqnarray}
自由度は、データ数が31つなので、31-4=27です。
データ数は31、そしてこの計算には各水準の平均を使っており、その水準の平均を出す際に、
例えば、水準1の平均を出す場合、1つ以外の値がわかればもとまるので、水準1についてはデータ9つで1個以外で確定するので、9-1
水準2は7-1、水準3は7-1、水準4は8-1
よって、自由度は(9-1)+(7-1)+(7-1)+(8-1) = 27
検定統計量
したがって、この後説明しますが、
検定統計量\(F\)は、
\begin{eqnarray}
F
&=& \displaystyle \frac{ \displaystyle \frac{S_{B}}{3} }{ \displaystyle \frac{S_{W}}{27} } \\
&=& 4.197 \\
\end{eqnarray}
有意水準を\(\alpha=0.05\)とした時、\(F_{0.05}(3,27) = \)であり、
検定統計量\(F\)について考察する
層間分散
層間分散とは、いくつかのグループ「間」の散らばり具合を意味します。あるグループとあるグループの距離が遠ければ遠いほど、相関が薄れていき、独立チックになります。
近しければ近しいほど、どちらのグループのデータかが分かりづらくなります。
ここで問題になるのは、じゃあそのグループ間とは言いつつも、何を基準としてその間を定義するのかですが、基本的には平均値になります。そのグループそれぞれの平均値をとって、その平均値同士の距離がグループ間の距離と定義します。
ではその水準間のばらつきはどう定義するか。
イメージとしては水準間なので、各グループ(水準)の代表値(ここでは平均値)を選び、それを確率変数としてみた場合の分散です。
なので、イメージとしては以下になります。
まず各グループの平均値は\(\bar{y}_{i}\)とします。\(i = 1,2,3,...,n\)
これを確率変数と見立てて、これらの平均値を\(\bar{y}\)とします。\(\displaystyle \bar{y} = \frac{1}{n} \sum_{i=1}^{n} \bar{y}_{i}\)
そうすると層間分散は、分散の定義から、
\begin{eqnarray}
S_{B}
&=& \sum_{i=1}^{n} (\bar{y}_{i} - E[\bar{y}])^{2} = \sum_{i=1}^{n} (\bar{y}_{i} - \bar{y} )^{2}
\end{eqnarray}
となります。
層内分散
次に層内分散ですが、これは各グループの中のデータの分散具合になります。
層内分散とは、層つまりグループ「内」でのデータの散らばり具合を意味します。いわゆる普通の分散のイメージです。
なので上と同様に今度は層の中の平均値を求めて、その平均値から各データの距離が分散になりますので、上と同じように分散を求めてみましょう!
まず各グループの平均値は上で定義したように、\(\bar{y}_{i}\)とします。\(i = 1,2,3,...,n\)
ここで、あるグループここではi=1にします。でこのグループでの分散を求めると、
\(\displaystyle \sum_{j=1}^{n_{1}} (\bar{y}_{1j} - \bar{y}_{1})^{2} \)
となります。
層内分散なので、各グループでの層内分散の和を求めると、
\begin{eqnarray}
S_{W}
&=& \sum_{i=1}^{n_{1}} (y_{1j} - \bar{y}_{1})^{2} + \sum_{j=1}^{n_{2}} (y_{2j} - \bar{y}_{2})^{2} +...+ \sum_{j=1}^{n_{n_{n}}} (y_{nj} - \bar{y}_{n})^{2} \\
&=& \sum_{i=1}^{n} \sum_{j=1}^{n_{j}} (y_{ij} - \bar{y}_{i})^{2} \\
\end{eqnarray}
(※ 判別分析での層内分散と層間分散と同じ考えなので一緒に覚えておくと良いです!)
検定統計量\(F\)について考察する
改めて、分散分析の検定統計量となるFは、
\begin{eqnarray}
F &=& \frac{層間分散(S_{B})}{層内分散(S_{W})}
\end{eqnarray}
です。
\(S_{T} = S_{B} + S_{W}\)の\(S_{T}\)の左辺\(S_{T}\)は\(F\)値を求める上では使用しません。
ここでは、この検定統計量について少し考察してみます。
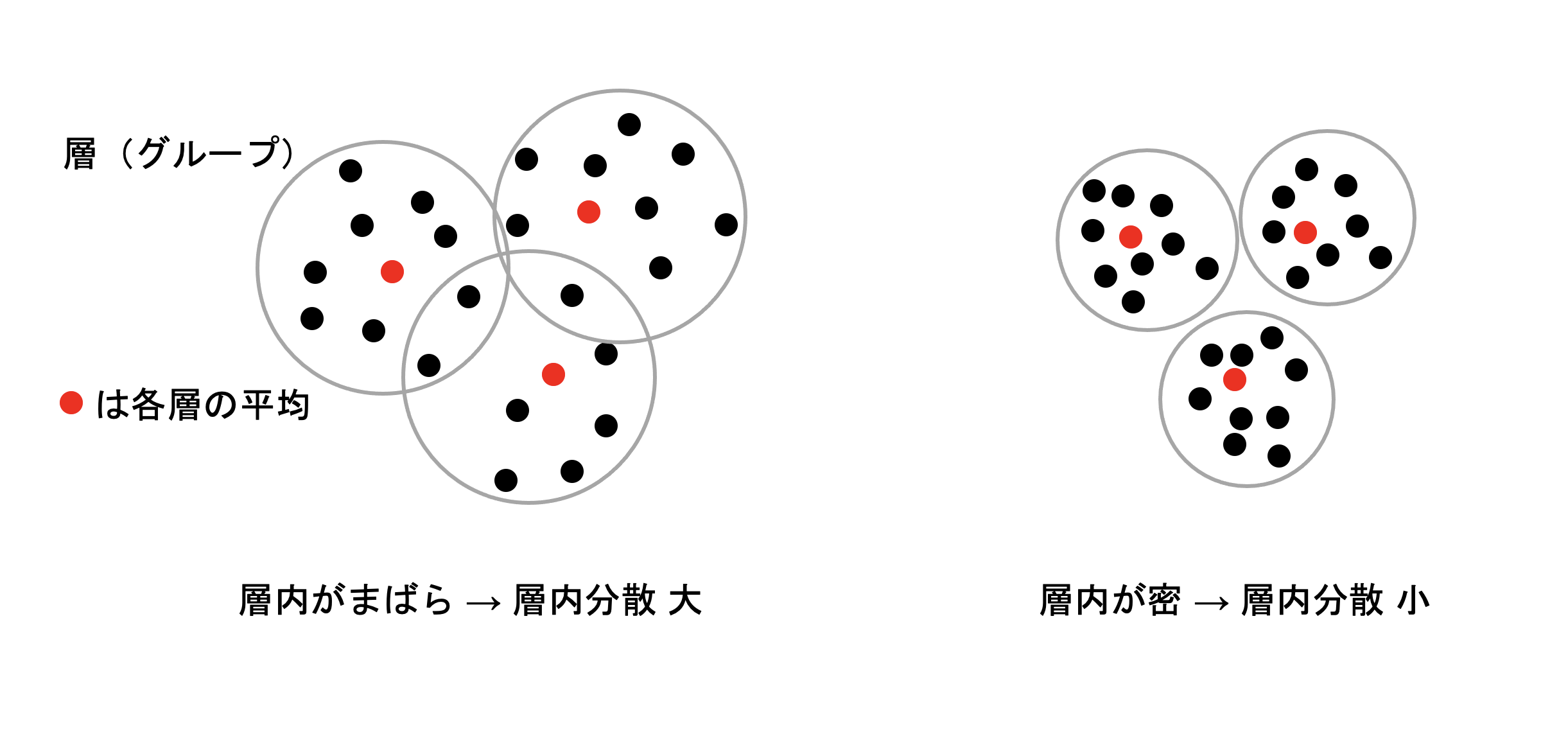
見た目、層間分散は同じに見えるので一定とした上で、層内分散は見た目で違うので、検定統計量の分母の違いで見ると、左の場合は検定統計量\(F\)は小さくなり、右の場合は大きくなります。
となると、右の場合は棄却されやすくなり、有意性が認められるということになります。
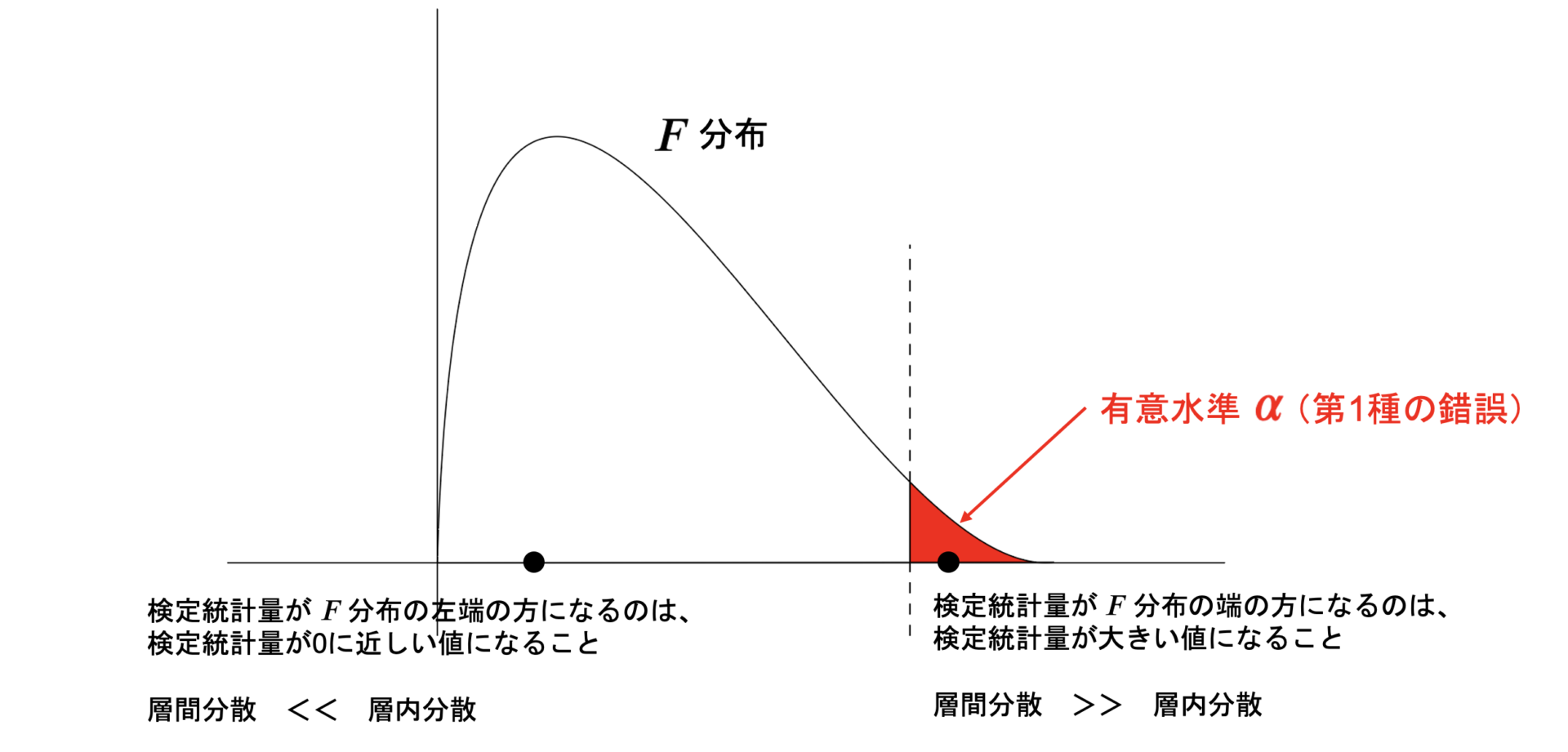
そんな層間分散と層内分散を用いて定義したこの検定統計量が大きくなると、\(F\)分布の端の方になるので、棄却域に行きそうということになります。
では端のほうに行くイメージはどういう時でしょうか。
上の分母が分子に比べて相対的に大きくなる場合ですが、分子が大きくなると、
間の距離が大きくなるので、グループ間が離れているということになり、そして分母が小さい場合は、
その1つ1つのグループ内でのデータの散らばりが小さいのでまとまってるイメージ。
イメージとしては以下のような感じですね。

となるとF値が大きいほど、グループ間での共通部分というか重なりの部分がなくなっていくので、流石にこれは平均一緒とは言えないよねってことで棄却ができるということになります。
検定統計量
\begin{eqnarray}
F
&=& \frac{S_{B}}{S_{W}} \\
&=& \frac{ \sum_{i=1}^{n} (\bar{y}_{i} - \bar{y} )^{2}}{\sum_{i=1}^{n} \sum_{j=1}^{n_{j}} (y_{ij} - \bar{y}_{i})^{2}} \\
\end{eqnarray}
そして層間分散の自由度は、k-1(kはグループ数)
層内分散の自由度は、n-k(kはグループ数)
有意水準を\(\alpha\)
よって、
\begin{eqnarray}
F
&=& \frac{\displaystyle \frac{S_{B}}{k-1} }{\displaystyle \frac{S_{W}}{n-k} } \\
&\sim& F_{\alpha}(k-1, n-k)
\end{eqnarray}
以下4つの正規分布から得たデータがあります。
それぞれの正規分布の平均値は以下の表のとおりで、それらの分布から採れたデータは\(y_{ij}\)とします。
この時、それぞれのクラスの合計値やデータ数、平均値は計算をして以下の通りとなります。
この時、それぞれのクラスで有意性があるかどうかをテストしてみましょう!
まずそもそも、この正規分布から得られた\(y_{ij}\)は、\(y_{ij} = \mu_{i} + \epsilon_{ij}\)と表現できます。
要は各正規分布の平均から、誤差をたすことでデータが生成されるといったイメージになります。
ここで考えたいのが、各水準の平均値\(\mu_{i}\)に差がないかどうかの検証です。
そのため、帰無仮説では、\(\mu_{1} = \mu_{2} = \mu_{3} = \mu_{4}\)と仮定して、
対立は実際の上記の表になります。
各水準の平均値に差がないのであれば、帰無仮説を採択して、有意な差があるのであれば帰無仮説を棄却(対立仮説を採択)ということになります。
これが分散分析の基本方針になります。
さまざまな分散分析
さまざまな要因によって、分散分析にも種類があります。
主には以下の3つがあります。
- 一元分散分析
- 二元分散分析
- 乱塊法
これらの違いとしては要因の数もありますが、以下のような要因にも種類があり、その組み合わせによっても変わります。
- 母数因子とは、因子水準を指定できるもの。
- 変量因子とは、因子水準を指定できないもの。
- 一元分散分析は、母数因子が1つ。
- 二元分散分析は、母数因子が2つ。
- 乱塊法は、母数因子が1つ+変量因子が1つ。
です。
1つずつ説明していきます。
一元分散分析
全てのデータ\(y_{ij}\)は、データの全平均\(\mu\)を基準として、各グループ平均と全平均の差分\(\alpha_{i}\)と各データごとに発生する誤差\(\epsilon_{ij}\)を加えた値になります。
なので、各グループごとに有意性がないとする場合、この\(\alpha_{i}\)の値が全て0であれば、全く有意性がないということになります。
\(y_{ij} = \mu + \epsilon_{ij}\)となり、全てのデータは全平均からの誤差の影響によるものと表現ができる。
(有意性があれば核水準の影響を受けているということになるので、上の式の通り、\(y_{ij} = \mu + \alpha_{i} + \epsilon_{ij}\)となる。)
二元分散分析
以下のような表になります。
例としては、以下のように要因が2つで、それぞれが水準が複数ある感じです。
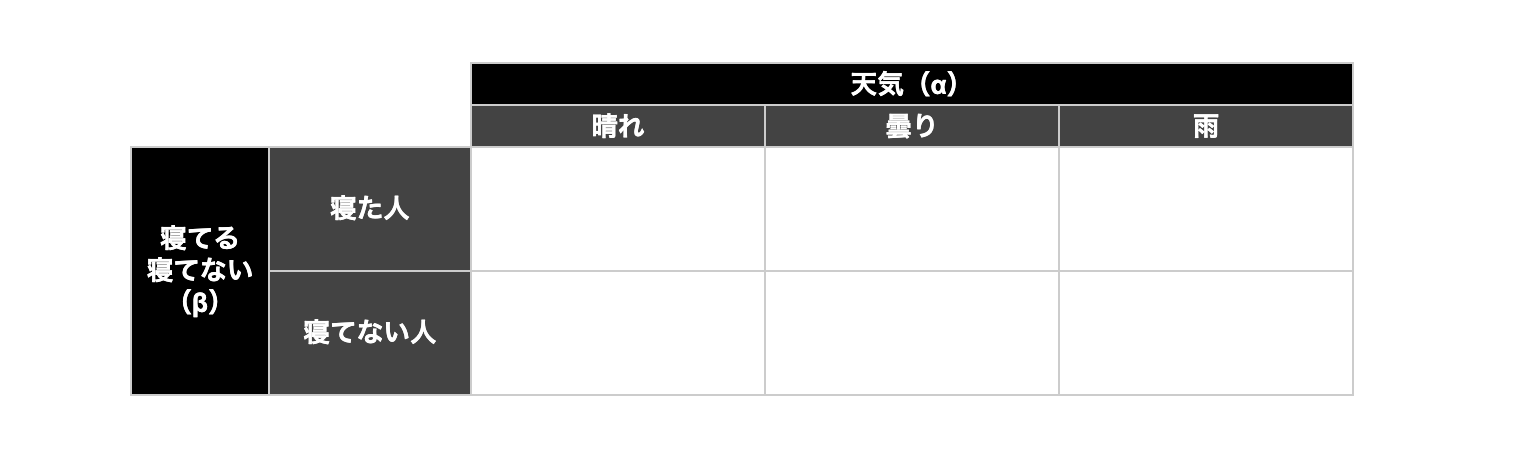
要因が2つでそれぞれ複数の水準がある場合です。
寝ている人で、その日が晴れの場合の集中力、
寝ている人で、その日が曇りの場合の集中力、、、
みたいな感じです。
上記のように2つの要因で水準があるので、母数因子2つの分析になります。
\(y_{ij} = \mu + \alpha_{i} + \beta_{j} + \gamma_{ij} + \epsilon_{ij}\)
まず、普通にそれぞれの要因の水準から影響を受けるので、\(\alpha_{i}\)と\(\beta_{j}\)を足します。
そして2つの要因がある場合、この2つが重なることで大袈裟ですが何かしらの化学反応で、影響を別に受ける可能性があります。そのため交互作用というものを考える必要があります。これを\(\gamma_{ij}\)として足します。
この違いはというと、
1つのみのデータの場合、そのデータがどういった要因によって生成されたかがわからない。
しかし複数のデータがある場合、そのデータを解析することで、A要因の影響なのか、B要因の影響なのか、さらに言えばAとBの組み合わせによって生まれた別の要因なのか(これを交互作用と言います)。
なので、二元分散分析では、この交互作用も考える必要があり、それが\(\gamma_{ij}\)になります。
どの要因なのかを特定するために、複数回試行します。
乱塊法
2つの要因があるので、\(\alpha_{i}(i=1,2,...,n)\)と\(\beta_{j}(j=1,2,...,m)\)とすると、
\(y_{ij} = \mu + \alpha_{i} + \beta_{j} + \epsilon_{ij}\)
なので有意性がAとBでないのであれば、
\(\alpha_{i}\)の値が全て0 かつ \(\beta_{j}\)の値が全て0
であれば、\(y_{ij} = \mu + \epsilon_{ij}\)となり、有意性がないということになります。
乱塊法とは、英訳すると「randomized block design」と呼ばれるように、ランダムなブロック、つまり実験の順序をランダム化するというものです。
乱塊法とは、変量因子という因子も取り入れて分散分析を行います。
変量因子の変動をとらえた上で、解析の精度を上げる手法です。
例えば道路の摩擦によって速度に影響も出たりしますが、実際摩擦がどれくらいとかの計測はできず、分析に入れることなどはできません。
つまり複数の水準に分けることなどができません。
なので、1つの要因に対して裏でこういった事情で、いくつかの道路の場所で計測しているのであれば、
それぞれの道路で要因の水準ごとに計測をしましょうよ!というのが乱塊法になります。
晴れと曇り、雨で道路の摩擦は全然違います。
なのに、とにかくデータを取るために、晴れの日に多く計測データをとって、曇りでは少なくデータをとって、雨は1件データとってとなる時に、
身長だとDNAなどそういった要因でも影響受けますが、その場合DNAの変動はとることはできません?
でも、これって2つの要因ということにはならないのか?
つまり2次元分散分析でできないのか?
となりそうですが、上でも話した通り、変量因子は水準指定ができないものということなので、
2次元での分散分析ができないということになります。
と言いつつも、できたりします。