ギブスさんプリンングを行う上で必要な処理としては以下のようなものが存在する。
マルコフ連鎖の話ではあるが絶対に必要かはわからない。
・マルコフ連鎖(最尤推定量と、斉次性、帰着性?
の性質については整理をする。
通常であれば、以下のように過去の情報から遡ってデータに影響を与える。
しかし、
マルコフ連鎖では1つ前の値を用いて、判断します。
そのような連鎖のことをマルコフ連鎖と言います。
マルコフ連鎖はいろんなところで使われています。
Contents
具体例
みなさんはよく、明日の天気は
調べない人だったり、天気どうでもいい人は、天気予報を見ず、今日晴れだったからおそらく晴れじゃないかなーとか、
少し曇ってたから曇りじゃないかなーとか、色々考えた上で結論を出しているかと思います。
はたまた、究極的に小学生時代の時にやった靴飛ばしで明日の天気を占ったりして、明日の天気を考えたりする方もいらっしゃるかもしれません。
今日はまさにその前者の考え方である、1つ前の日がこうだったら、次はどうなるのかなという連鎖的なことを考えていきます。
マルコフ連鎖の例
先程あげた天気を例にして話していこうと思います。
天気は晴れが続いたり、さらには曇りが続いたり、でも次の日は晴れたりと様々な変化を見せてくれます。
状態変化ですね。
当然シーズナリティによって、雨が多く続く日として梅雨や夏があったり、冬では雪が降ったり、ジオロケーションによっても変わりますが、
あくまでここの例ではひとまず純粋に晴れなのか、曇りなのか、雨なのかをマルコフ連鎖で考えてみたいと思います。
天気の晴れ、曇り、雨のやつで、
晴れから曇りの条件付き分布
まず
p(曇り|晴れ)*P(晴れ)
P(晴れ)は条件付きとかではなく、純粋の晴れが出る確率(前日がどうだったかどうかは関係ない)
なので、
全体のうち、晴れが出た回数で確率を算出します。
例えば、ある1年で、
1年間のうち晴れが80回なら、確率は80/365となります。
単純に集計して、晴れ、曇り、雨、雪の確率を出すイメージです。
これによって、
\begin{eqnarray}
P(晴れ) &=& ・・・①\\
P(曇り) &=& \\
P(雨) &=&
\end{eqnarray}
というように算出されます。
そして前日が晴れの時、今日が曇りになる確率は、
1 2 3
晴 曇 晴
というデータがあった時、
全ての組み合わせから、出す。
1->2のように晴れ→曇の回数を出して、365で割って確率を出します。
そして以下のような確率が出たとします。
\begin{eqnarray}
P(晴れ|晴れ) &=& 0.4\\
P(晴れ|曇り) &=& 0.3\\
P(晴れ|雨) &=& 0.3\\
\\
P(曇り|晴れ) &=& 0.4\\
P(曇り|曇り) &=& 0.4\\
P(曇り|雨) &=& 0.5\\
\\
P(雨|晴れ) &=& 0.2\\
P(雨|曇り) &=& 0.3\\
P(雨|雨) &=& 0.2\\
\end{eqnarray}
これによって、今日雨だった場合、次の日が晴れになる確率など、
1つ前の天気によって今日がどんな天気になるのかの確率が出ました。
では、晴れだった日の2日後は晴れになる確率はどうなるでしょうか?
こういった時系列を考えた上で、どうなるかを予測するのをマルコフ連鎖です。
まず今日晴れが出る確率は、①から\(P(晴れ)\)です。
そして、晴れが出て翌日はどんな天気が出てもいいです。結果的に2日後に晴れになる確率を求めるので。
なので、
今日晴れが出たとして、翌日に晴れになる確率は\(P(晴れ|晴れ)\)
翌日に曇りになる確率は\(P(曇り|晴れ)\)
翌日に雨になる確率は\(P(雨|晴れ)\)
です。
これらは互いに排反で同時に起こり得ない(次の日の天気が同時に晴れ、曇り、雨になることはない。お天気雨とか晴れのち曇りとかは考えないとして)
そして、2日後には晴れになるので、
翌日晴れだった時、その翌日つまり2日後が晴れになる確率は、\(P(晴れ|晴れ)\)
翌日曇りだった時、その翌日つまり2日後が晴れになる確率は、\(P(晴れ|曇り)\)
翌日雨だった時、その翌日つまり2日後が晴れになる確率は、\(P(晴れ|雨)\)
よって今日晴れだった時、2日後も晴れになる確率は、
\begin{eqnarray}
P(晴れ|晴れ)*P(晴れ|晴れ)*P(晴れ) + P(晴れ|曇り)*P(曇り|晴れ)*P(晴れ) + P(晴れ|雨)*P(雨|晴れ)*P(晴れ)
\end{eqnarray}
行列表記
上の式は実は行列表記すると簡単に表現が可能です。
上では晴れを基準に求めてました。でも行列を使うことで簡単にまとめて計算処理が可能になります。

行に現在の起点の値を置いて、列に次に起こる値を置きます。

\((1,1)\)では\(P(晴れ|晴れ)\)とありますが、これは晴れだった時に、晴れになる確率で、\(t\)期で晴れだった時、\(t+1\)期で晴れになる確率を表しています。
なのでこの行列は各天気から次の天気を予測するための確率を表したもので、\(t\)期から\(t+1\)期へ遷移するという意味も含めて、遷移核と呼んだりします。
そして行列は線形代数で、写像という意味が込められています。
写像とはあるベクトルに対して行列をかけることで、別のベクトルへ変化を加える(移動させる)という性質を持っています。
なので、\(t\)期の天気から\(t+1\)期の天気の確率予測を出す際は、\(t\)期でのベクトルに対して、上記の行列をかけることで\(t+1\)期での予測を出すことができるということです。
上記の行列を\(P\)とした時、
\(x_{t+1} = P x_{t}\)
\begin{eqnarray}
P =
\begin{pmatrix}
0.4 & 0.4 & 0.2 \\
0.3 & 0.4 & 0.3 \\
0.3 & 0.5 & 0.2 \\
\end{pmatrix}
\end{eqnarray}
\(t\)期が晴れであれば、
\begin{eqnarray}
x_{t} =
\begin{pmatrix}
1 \\
0 \\
0 \\
\end{pmatrix}
\end{eqnarray}
とします。
そして\(t+1\)期の天気ベクトルを\(x_{t+1}\)とすると、\(x_{t+1} = P x_{t}\)となります。
実際に当てはめて計算をしてみます。\(t\)期では晴れだったとした時、\(t+1\)では、
\begin{eqnarray}
x_{t+1}
&=& P x_{t} \\
&=&
\begin{pmatrix}
0.4 & 0.4 & 0.2 \\
0.3 & 0.4 & 0.3 \\
0.3 & 0.5 & 0.2 \\
\end{pmatrix}
\begin{pmatrix}
1 \\
0 \\
0 \\
\end{pmatrix}
&=&
\begin{pmatrix}
0.4 \\
0.3 \\
0.3 \\
\end{pmatrix}
\end{eqnarray}
になります。
そもそも、tからt+1という1つ先に遷移するだけなので、そもそもの上の確率と一致するのは当然ですね笑
では2つ先の、tからt+2という2つ先に遷移した場合はどうなるでしょうか。その場合は遷移行列\(P\)を2回かけてあげればよいです。
それは、\(x_{t+1} = P x_{t}\)から\(x_{t+2} = P x_{t+1}\)になり、\(x_{t+2} = P^{2} x_{t}\)となるからです。
ここでt期を晴れとして計算してみると、
\begin{eqnarray}
x_{t+2}
&=& P^{2} x_{t} \\
&=&
\begin{pmatrix}
0.4 & 0.4 & 0.2 \\
0.3 & 0.4 & 0.3 \\
0.3 & 0.5 & 0.2 \\
\end{pmatrix}
\begin{pmatrix}
0.4 & 0.4 & 0.2 \\
0.3 & 0.4 & 0.3 \\
0.3 & 0.5 & 0.2 \\
\end{pmatrix}
\begin{pmatrix}
1 \\
0 \\
0 \\
\end{pmatrix}
&=&
\begin{pmatrix}
0.4 \\
0.3 \\
0.3 \\
\end{pmatrix}
\end{eqnarray}
となります。
このように現時点tからt+2という2つ先の各種晴れ、曇り、雨の予測確率をマルコフ連鎖で出すことができました。
計算式をもう少し深ぼってみると、
確率の掛け算と足し算が混在しています。
掛け算はまさに同時に成立しないといけないものです。足し算は互いに排反だから。
このように、マルコフ連鎖はn先を予測するとなると、\(x_{t+n} = P^{n}x_{t}\)となります。
行列でも1つ前のデータしか考えていないので、マルコフ連鎖は1つ前のデータで予測する連鎖するということがわかります。
ただこのような仮定を置くことで、さまざまな性質があります。
もちろん何回も処理(n回を無限)をしていけば確率収束により、不変分布と呼ばれる完全な予測モデルができます。
マルコフ連鎖を一般化する
上記の天気のマルコフ連鎖を用いて一般化してみます。
\begin{eqnarray}
P(x_{ac}^{2}) = P(X_{n+2} = c | X_{n} = a)
\end{eqnarray}
とします。X_{n}をあるn時点での値を示し、X_{n+2}をn時点から2回試行した際の値を示します。
そしてこの時、acはn時点でaだったとき、n+2時点ではcになる確率を示します。
上の天気の例であった通り、間はなんでもよかったので、今回の場合だとn+1時点の値はなんでも良いです。
\begin{eqnarray}
P(x_{ac}^{2}) = P(X_{n+2} = c | X_{n} = a)
\end{eqnarray}
そして最終的に求めたいのが、この思考を無限にして行った時に値が収束するわけです。
要は
マルコフ連鎖の性質
上記でマルコフ連鎖の概要については大まかわかったところで、ここではマルコフ連鎖の性質について説明します。
マルコフ連鎖を考えていく上で重要な性質は以下の4つになります。
- \(①\) 非周期的
- \(②\) 再帰性
- \(③\) 規約性
- \(④\) 不変性
\(①\) 非周期的
\({n : p_{ii}^{(n)} > 0}\)の最大公約数が1であること。
周期というのは通常、1年は12ヶ月あって、また12ヶ月経てば新しい年になります。
さらにメトロノームは左端から、右端を経由してまた左端まで戻ってくる時間はほぼ同じです。
周期とは同じ時間が経てばまた戻ってくることを言います。
そしてこのマルコフ連鎖の非周期的というのは、その名の通り周期ではないので、
同じ時間で同じ地点に戻ってくる事がないということになります。
ある地点から10回遷移したらまたその地点に戻ってきて、さらにまた10回遷移したら同じ地点に戻ってきて、、という繰り返しの遷移がないということになります。
\(②\) 再帰性
\(n > 1\)で\(p_{ii}^{(n)} > 0\)となることである。
つまり、\(p_{ii}\)なので\(i\)から\(i\)へ、つまり同じ地点に\(n\)つまり\(n\)回した後に0より大きいということは確率は0ではないということなので、
状態\(i\)から状態\(i\)に何回か(\(n\)回)した後に、戻ってくる確率は0より大きいので、いつかは必ず戻ってくるということになります。
ここで状態\(i\)は「任意」なので、全ての状態\(i\)で成立する必要がある。
再帰性とはある地点から移動して、またその地点にいつか戻って来れるということ。
再び帰れると書いて再帰性。
マルコフ連鎖が再帰性を持つということは、1つでもその地点にはもう一生戻って来れない場合があるときは、再規制とは言わない。
例えば、
A→B,C,Dで、B, C, Dの間でぐるぐる回ってて、B,C,DからAにいくことがない場合、
最初Aにいるけど、一生もうAにいくことができないので、これは再帰性があるとは言えない。
エルゴート性
ここで1つ。エルゴート性について。
エルゴート性とは上の非周期的かつ再帰性をもったマルコフ連鎖のことを言います。
上記2つを持つことでエルゴート性を持ったと言えます。
\(③\) 規約性
任意の\(i,j\)に対して、\(p_{ij}^{(n)} > 0\)となる正の整数\(n\)が存在すること。
上の文章をもう少し噛み砕くと、
\(p_{ij}^{(n)}\)は状態\(i\)にいて、\(n\)ステップ後に状態\(j\)にいる確率が0より大きい、つまりどんだけ状態移動したとしても(\(n\)が大きくなっても)、いつかはたどり着くということが言えます。
そして「任意の\(i,j\)に対して」なので、状態\(i\)や\(j\)がどれだとしてもこれが成立するということになるので、該当のマルコフ連鎖で考えている全ての状態が行き来できることということになります。
再帰性は\(ii\)ということで、同じ地点に戻って来れるということでした。
この規約性は\(ij\)ということで、状態\(i\)から状態\(j\)にいつか推移できるということです。
状態\(i\)から状態\(j\)への推移は地点を結べば直接で推移できるが、そういうことではなく、何回か遷移して状態\(j\)に行けるのであればOKです。
直接でも良いし、何回か遷移して状態\(j\)に行けるでもOK。つまり直接が結ばれてなく遷移できなくても、遠回りして遷移できればOKということです。
ではどのような場合に規約性がないか。
以下のように地点が独立してポツンとある状態です。例で、A,B,C,D,Eで構成されて、独立してX,Yがあるみたいな。
この場合、どんなに遷移しても繋がっていないので、遷移できないですね。。
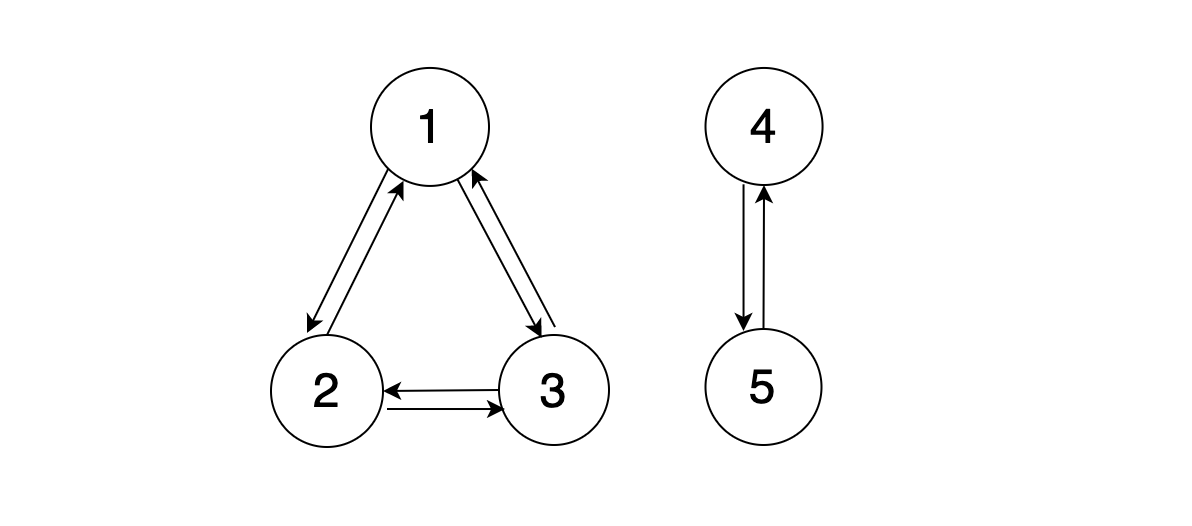
以下の場合は繋がってるので規約性あるのではと思いそうですが、4から5へはいけません。
1からも4を経由して5へはいくことができません。
そのため、任意の状態\(i\)から別の任意の状態\(j\)へ移ることができるわけではないので、規約性はないことになります。
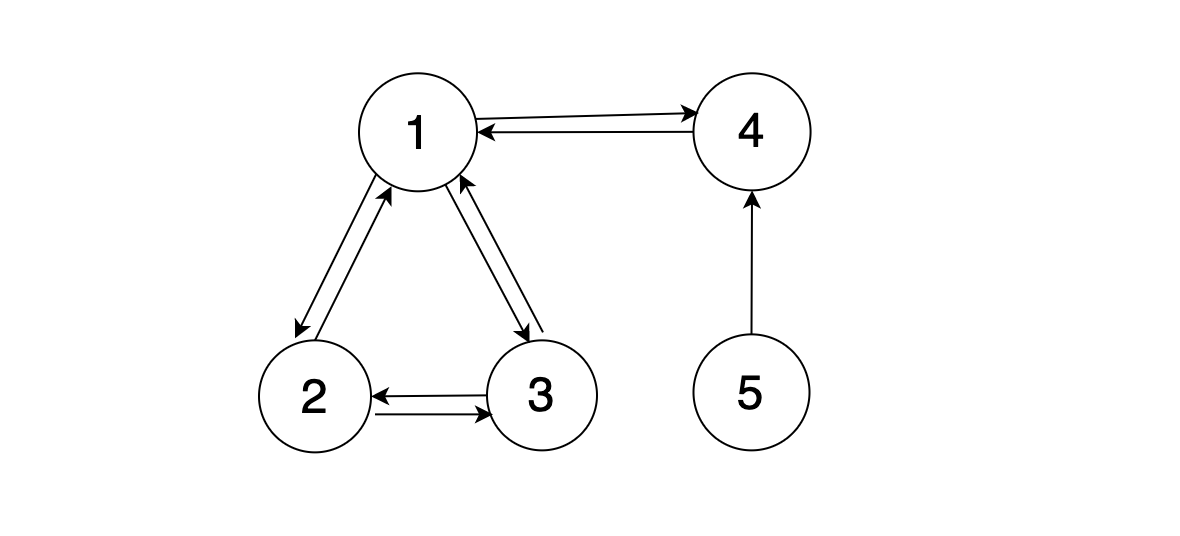
以下の場合だと、3から5がつながっていて、3→5→4→1というように流れができているので、任意の状態\(i\)から別の任意の状態\(j\)へ移ることができることになるので、規約性はあるということになります。
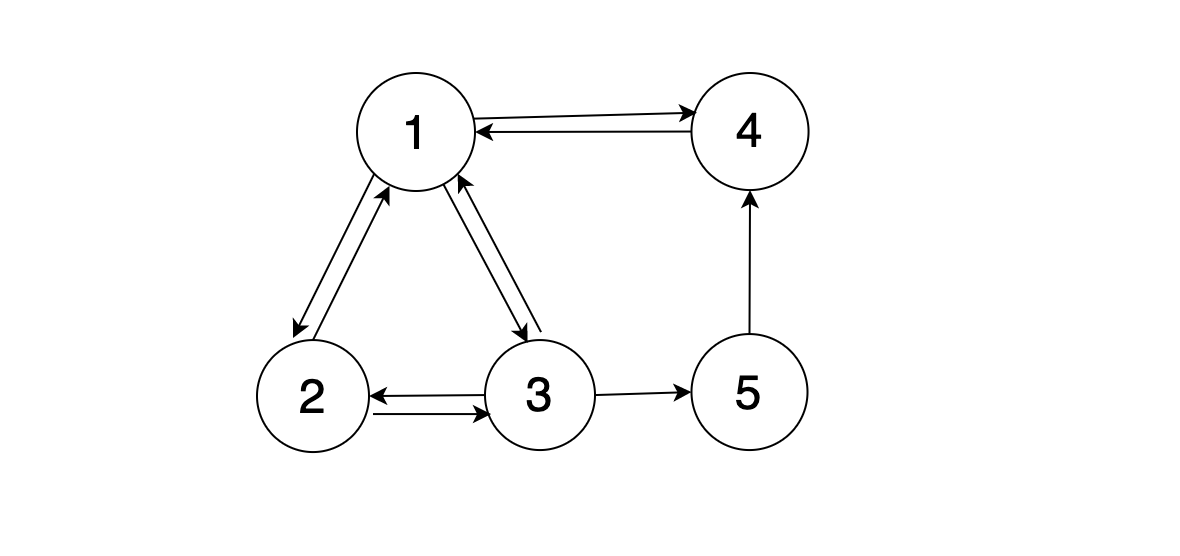
状態\(i\)から状態\(j\)へ0より大きい確率で遷移できる、なので何回かすれば必ず状態\(i\)から状態\(j\)へいく事ができるという事です。
任意なので、上の晴れ、曇り、雨とあれば、
\((i,j)\)の組み合わせは、\((i,j)=\)(晴れ, 曇り),(曇り, 雨),(雨, 晴れ),(の6通りでそれぞれ成立する必要があります。
注意は、\(ij\)は状態\(i\)から状態\(j\)に行ける確率であり、この\(i,j\)には晴れ、曇り、雨が入ります。なので、状態\(i\)が晴れ、状態\(j\)が雨で確率があったとしても、状態\(i\)が雨、状態\(j\)が晴れの場合も考えないといけません。もしかしたら一方通行で晴れから雨はあるが、雨から晴れは絶対に起こり得ないみたいな事がある場合は、規約性は成立しません。
規約性はなので、どこかの遷移の線をもうこれ以上切ってしまうと完全にその島に行けなくなってしまう場合が規約性と呼べます。
エルゴート的なマルコフ連鎖
さらにここで、再度エルゴート性を考えます。
エルゴート性は非周期性と再帰性を持てばそのマルコフ連鎖はエルゴート性と言いました。
これに加えて、規約性ももつマルコフ連鎖は、「エルゴート的なマルコフ連鎖」と呼びます。
\(④\) 不変性(定常分布)
エルゴート的なマルコフ連鎖では、以下の重要な不変性という性質を持ちます。
任意の\(i,j\)に対して「\(\pi_{i}p_{ij} = \pi_{j}p_{ji}\)」が成立する、確率ベクトル\(\pi = (\pi_{1},\pi_{2}, ..., \pi_{n})\)が存在する時、マルコフ連鎖は可逆と呼び、この時の\(\pi\)は不変分布と呼びます。
\(\pi = P\pi\)が成立する。
※ 「\(\pi_{i}p_{ij} = \pi_{j}p_{ji}\)」は詳細釣り合い条件と呼ばれる。
例えば梅雨の時期を考えると、その時期では雨の確率が高くなります。
なので最初に梅雨の時期からマルコフ連鎖を考えると、かなり雨の影響を受けるかと思います。
しかしだんだん月日も流れてマルコフ連鎖の遷移数もかなり増えていくと、あまり確率ベクトルの数値が変わらず収束していきます。
いわゆる大数の法則みたいにサンプル数が増えれば確率も自ずと収束していくというイメージです。
確率ベクトルはいわゆる\(\pi = (晴れの確率、曇りの確率、雨の確率)\)です。
そして\(p\)は晴れから曇りなど、天気を移動させる確率です。
「任意の\(i,j\)に対して」とあるので、晴れ、曇り、雨それぞれが収束してもう確率ベクトルの値がどれも変わらない状態になる必要があります。
マルコフ連鎖では推移行列\(P\)によって、確率ベクトル\(\pi\)は変わっていきます。
変わっていくと、だんだんある値に収束していき、それを\(\pi^{*}\)とすると、そのとき推移行列\(P\)をかけても、変わらず、\(\pi = P\pi\)が成立します。
最初の確率ベクトルを\(\pi_{1}\)とすると、\(P\pi_{1} = \pi_{2}\)、\(P\pi_{2} = \pi_{3}\)、\(P\pi_{3} = \pi_{4}\)、、、、と変わっていきます。
そしていつか、\(P\pi = \pi\)となる分布が出ると仮定します。
これがいわゆる不変分布で、一度でも\(\pi\)が出てしまったら、それ以降推移行列\(P\)を掛けても、\(\pi\)になり続けます。
初期状態を\(\pi_{1}\)、\(n\)ステップ後の状態を\(\pi_{n}\)とすると、
\begin{eqnarray}
\left\{
\begin{array}{l}
\pi_{2} = P\pi_{1} \\
\pi_{3} = P\pi_{2} \\
\pi_{4} = P\pi_{3} \\
\cdot \cdot \cdot \\
\pi_{n+1} = P\pi_{n}
\end{array}
\right.
\end{eqnarray}
繰り返し代入をしていくと、\(\pi_{n+1} = P\pi_{n} = P(P\pi_{n-1}) = P(P(P\pi_{n-2}) = \cdot \cdot \cdot = P^{n}\pi_{1}\)で、
\(\pi_{n+1} = P^{n}\pi_{1}\)
となります。
ここでpは提案分布と呼ばれたりします。
pは上で説明してきた通り、ある状態からある状態へ遷移をさせる分布みたいなもので、このpによって様々な確率で晴れだった時、雨になる確率(今いる地点/今いる確率変数から、別の地点/別の確率変数に移動する確率)を
ちなみに確率ベクトルは、初期値の晴れ自体の確率、雨自体の確率、曇り自体の確率のこと。初期分布と言ったりもします。
1回遷移すると、晴れの確率は変わってきたりする。
これを繰り返すと、真の晴れの確率などが出て収束していくイメージです。
不変分布と聞くと、よく\(\pi = P\pi\)という表現のものが出てきます。
これももちろんあっており、今の地点から提案分布Pによって移動した結果、また同じ\(\pi\)に移動するということなので、無限ループとなり、不変状態になります。
この詳細釣り合い条件でも同じで、今いるところから別のところに移動する確率と、その別のところから今いるところに移動する確率が同じということを示しています。同じであれば今いるところと別のところが同じところにいることになるので、結果的に不変状態ということになります。
表現方法はいくつもあるので注意が必要です。
もちろんどんな分布も不変性を持つわけではないです。
粒子などで、こっちに移動してもまたこっちに移動してと常にあるところを行ったり来たりしてしまう状態が平衡状態と呼びますね。
これが成立すると、もうここから移動できなくなってしまい均衡状態になるので、この時の分布を定常分布や不変分布と呼びます。
詳細釣り合い式と呼びます。
(ギブスサンプリングとかで使います)
不変分布はどういう時に持つか?
不変分布は、上で扱った「エルゴート的なマルコフ連鎖」であるマルコフ連鎖において、不変分布を持つと証明されてます。
\(\pi = (\pi_{1}, \pi_{2}, ..., \pi_{n})\)とします。
「エルゴート的なマルコフ連鎖」では任意の\(i\),\(j\)で
\begin{eqnarray}
\pi_{j} = \lim_{n \rightarrow \infty} p_{ij}^{n}
\end{eqnarray}
が存在する。\(\pi\)は\(P\)の定常分布になる。