わかりやすいベルヌーイ分布

ここでは、有名な離散分布の第1弾として、

• ベルヌーイ分布
• 二項分布

について話していこうと思います。
 

ベルヌーイ分布

ベルヌーイ分布の確率密度関数は以下です。

ベルヌーイ分布は1回の試行で、正が出る確率のことをいいます。
つまり、1回何かをやった時、起こる場合と起こらない場合のような2つに事象を分けた場合の確率を意味しています。

ベルヌーイ分布の確率関数は以下となります。
$$
P(X=k) = p^{k}(1-p)^{1-k}
$$

コインを投げた時、表が出るとき\(X=1\)、裏が出るとき\(X=0\)とすると、
表が出る時\(k=1\)を代入すると、\(P(X=1) = p\)となり、表の出る確率を表し、
裏が出る時\(k=0\)を代入すると、\(P(X=0) = 1-p\)となり、裏の出る確率を表しています。

期待値\(E[X]\)と分散\(V(X)\)の計算

確率変数\(X\)の期待値は、
確率変数のとりうる値は0と1で、それぞれの出る確率は\(1-p\)、\(p\)なので、
$$
E[X] = 0 \cdot (1-p) + 1 \cdot p = p
$$
となります。

確率変数\(X\)の分散は、分散は期待値(平均)からの確率変数の値の距離なので、
\begin{eqnarray}
V(X) &=& (0 - E[X])^{2}(1-P) + (1 - E[X])^{2}p \\
&=& p^{2}(1-p)+(1-p)^{2}p \\
&=& p^{2}-p^{3}+p-2p^{2}+p^{3} \\
&=& p-p^{2} \\
\end{eqnarray}
 

二項分布

ポアソン分布の確率密度関数は以下です。

二項分布とは、「2つの事柄に対して、\(n\)回試行した時、片方が\(k\)回出る確率のこと」を言います。
 
主な事象例としては、2つの事柄なので、コインの裏表を考えた時、
\(n\)回コインを投げた際に\(k\)回表が出る確率のこと。

二項分布は確率変数はこの1回の試行の表か裏ではなく、
n回の試行した結果表が何回出たかが確率変数になります。
なので、
$$
X=X_{1}+X_{2}+...+X_{n}
$$
この\(X_{1}\)、\(X_{2}\)、...は1回投げて表か裏なのでベルヌーイ分布です。

 
さらには無理やり2つの事柄にして考えると、例えばサイコロ。
サイコロで1,2,3,4が出た場合を表とし、5,6が出た場合を裏とすれば、サイコロも2つの事柄になります。
 
このように世の中のいろんな事象を2つの事柄に置き換えると、この分布を利用してさまざまな計算ができる特徴があります。
 
$$
P(X=k)={}_nC_k p^ k(1-p)^{n-k}
$$
 

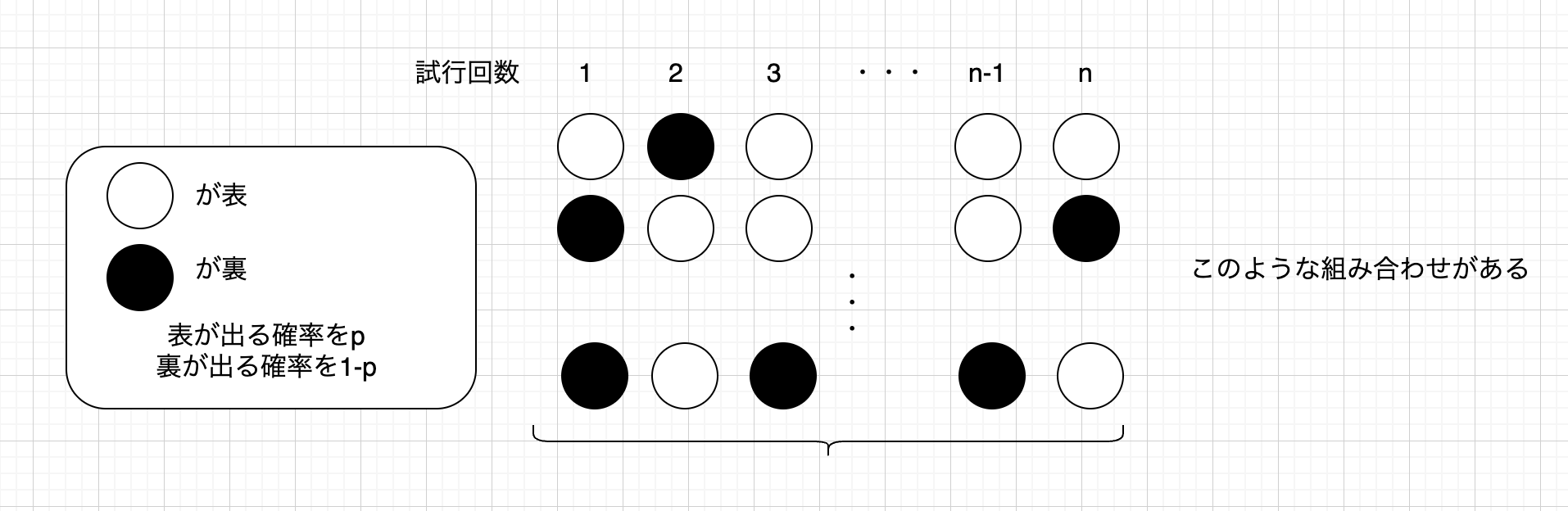
この式の導出について、考えてみます。
 

上の図を見ながら、説明していきます。

試行回数\(n\)回うち\(k\)回表が出るとします。
でも何回目で表が出るかわかりません。
ただ、\(k\)回表が出るということは、\(n-k\)回は裏が出ると分かります。
 

\(①\) まず出る順番（上の図）の組み合わせは、\({}_nC_k\)通り。
\(②\) そして、表が出る確率は\(p\)で同時に表が今\(k\)回出るので、確率の積により\(p^{k}\)。
\(③\) そして、裏が出る確率は\(1-p\)で同時に裏が今\(n-k\)回出るので、確率の積により\((1-p)^{n-k}\)。
 

これらは同時に起きるので、全てを掛け算して、
\(P(X=k)={}_nC_k p^ k(1-p)^{n-k}\)
となります。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

#二項分布乱数
n =100
p =0.4
data_rb= np.random.binomial(n, p, size=1000)
print(data_rb)

bins = np.arange(20, 60)-0.5
plt.hist(data_rb, bins, density=True)

#二項分布理論値
from scipy.stats import binom
#x: data_rbの範囲...integer
k = range(min(data_rb),max(data_rb))
binom_pmf = binom.pmf(k, n, p)

plt.plot(k, binom_pmf)

 
二項分布のモーメント母関数
期待値と分散
 
確率関数の形を見ると、
二項分布とベルヌーイ分布の形は似ています。
それもそのはず、両方とも表と裏のような相反する事象(2つの事象が出るかどうか)と、二項分布は試行回数が複数回、ベルヌーイ分布は1回のみ。
なので、二項分布の関数にn=1を入れると、ベルヌーイ分布と同じ確率関数になります。
 

二項分布のモーメント母関数

以下※にて、パスカルの三角形を用います。

\begin{eqnarray}
M(t)
&=& E[e^{tx}] \\
&=& \sum_{x=0}^{\infty} e^{tx}\cdot P(X=x) \\
&=& \sum_{x=0}^{\infty} e^{tx}\cdot {}_nC_x p^x (1-p)^{n-x} \\
&=& \sum_{x=0}^{\infty} {}_nC_x (e^{t}p)^x (1-p)^{n-x} ・・・※ \\
&=& \{ (e^{t}p) + (1-p) \}^{n} \\
\end{eqnarray}
 

二項分布の期待値

\begin{eqnarray}
M^{'}(t)
&=& \{ (e^{t}p) + (1-p) \}^{n(')} \\
&=& n(e^{t}p + 1-p)^{n-1} \cdot (e^{t}p + 1-p)^{'} \\
&=& ne^{t}p(e^{t}p + 1-p)^{n-1} \\
\end{eqnarray}

\begin{eqnarray}
E[X]
&=& M^{'}(0) \\
&=& ne^{0}p(e^{0}p + 1-p)^{n-1} \\
&=& np(p + 1-p)^{n-1} \\
&=& np \\
\end{eqnarray}
 

二項分布の分散

\begin{eqnarray}
M^{''}(t)
&=& \frac{d}{dt} M^{'}(t) \\
&=& np e^{t} (e^{t}p + 1-p)^{n-1} + np e^{t} (n-1)(e^{t}p + 1-p)^{n-2} \cdot e^{t}p \\
&=& np e^{t} (e^{t}p + 1-p)^{n-1} + n(n-1) p^{2} e^{2t} (e^{t}p + 1-p)^{n-2} \\
\end{eqnarray}

\begin{eqnarray}
M^{''}(0)
&=& np e^{0} (e^{0}p + 1-p)^{n-1} + n(n-1) p^{2} e^{0} (e^{0}p + 1-p)^{n-2} \\
&=& np(p + 1-p)^{n-1} + n(n-1) p^{2}(p + 1-p)^{n-2} \\
&=& np + n(n-1) p^{2} \\
\end{eqnarray}
 

したがって、
\begin{eqnarray}
V(X)
&=& E[X^{2}] - \{E[X]\}^{2} \\
&=& M^{''}(0) - \{M^{'}(0)\}^{2} \\
&=& ( np + n(n-1) p^{2} ) - n^{2}p^{2} \\
&=& ( np + n^{2}p^{2} - np^{2} ) - n^{2}p^{2} \\
&=& np - np^{2} \\
&=& np(1-p) \\
\end{eqnarray}