ここでは離散の確率分布である、「負の二項分布」について話していこうと思います。
負の二項分布はあまり統計学の分野でそこまで取り上げられるものではないですが、簡単にここで説明できればと思います。
負の二項分布
負の二項分布は、決められた回数、裏が出たらそこで終了というもの。
つまり、幾何分布は一回出ただけで終了だが、負の二項分布は決められた回数出たら終了。
式についてはいろんな書き方がありますが、以下の書き方は1つの例です。
負の二項分布の確率密度関数は以下です。
\begin{eqnarray}
P(X=x)= {}_{r+x-1}C_{x}p^{r}(1-p)^{x}
\end{eqnarray}
負の二項分布の導出
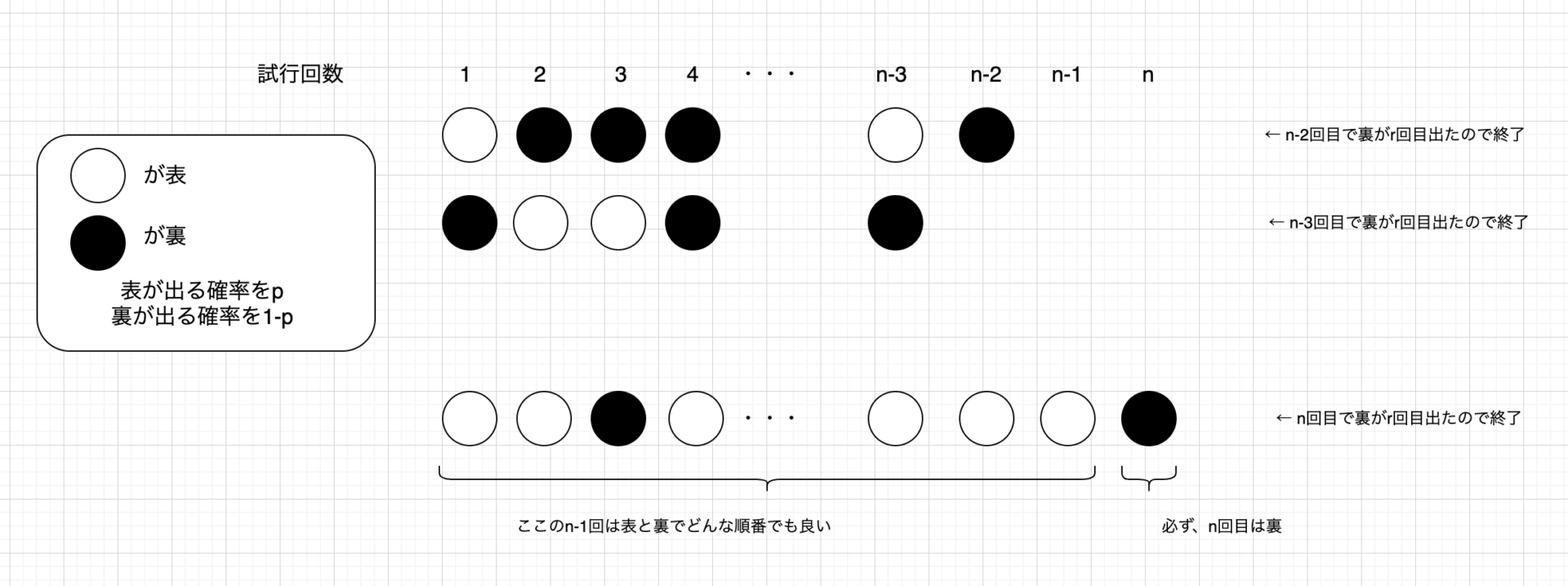
上の図を見ながら、説明していきます。
コイントスを行っていき、裏が\(r\)回出た時に終了する場合を考えます。そしてその時の表の出た回数を\(x\)とします。
そして、表の出る確率を\(p\)として、裏を\(1-p\)とします。
この場合、以下のことが言えます。
- 裏が\(r\)回出た時に終了するということは、最後のコイントスは\(r\)回目の裏が出たということ。
- 最後のコイントスでは裏が出ているので、その前までに裏は\(r-1\)回出ており、表は\(x\)回出ている。そして\(r-1\)回までの裏、表の出る順番はなんでも良い。
どんな場合でも必ず最後は\(r\)回目の裏で終了することが大事です。
まず裏\(r-1\)回、表\(x\)回の順番を考えます。
区別はないので、そのままコンビーネーションで、試行回数\(x+(r-1)\)回でその中で表が\(x\)回出る組み合わせは、\({}_{x+(r-1)}C_{x}\)通り。
そして表が\(x\)回出るので、\(p^{x}\)
裏が\(r\)回出るので、\((1-p)^{r}\)
これらは同時に成立するので、掛け算により、
\begin{eqnarray}
P(X=x)= {}_{r+x-1}C_{x}p^{r}(1-p)^{x}
\end{eqnarray}