\(N(\mu,\sigma^{2})\)

今回は、時系列データや金融工学などでよく用いられるブラウン運動という概念についてご紹介します!
ブラウン運動は統計学的にも応用的な分野で初学者にとっては難しい内容になります。
さらに今までは確率変数という1つの値を取るようなイメージで扱ってきましたが、
ここではパスという新しい概念を使って運動を考えていきます。
このパス、英語で道という意味で、このパスが今回は確率変数になります。
ちょっと違った角度で確率変数としてとらえたり、より世の中の時系列データをどう捉えるかが大事になってくるので、ここで学んでいきましょう!
ブラウン運動とは
まずは早速ブラウン運動の定義です。
ブラウン運動の定義
(統計学ワークブックから参照)
確率過程\(X=(X_{t})_{t>0}\)が以下の(1),(2)を満たすとする。
(1) 任意の\(0 = t_{0} < t_{1} < \cdot \cdot \cdot < t_{n-1} < t_{n}\)に対して、\(X_{t_{0}}, X_{t_{1}} - X_{t_{0}}, X_{t_{2}} - X_{t_{1}}, ..., X_{t_{n}} - X_{t_{n-1}}\)は互いに独立である。(独立増分性) (2) 任意の\(0 < y < t+h\)に対して、\(X_{t+h} - X_{t}\)の分布は\(X_{h} - X_{0}\)の分布と同一である。(定常増分性)
\(B_{0} = 0\)なる確率過程\(B=(B_{t})_{t>0}\)が以下の(1)〜(3)の性質を満たすとき、\(B\)をブラウン運動という。
(1) \(B\)は独立定常増分過程である
(2) 各\(t>0\)に対して、(周辺分布)\(B_{t} \sim N(\mu t, \sigma^{2}t)\)
(3) \(B\)のパスは連続である。
【標準ブラウン運動】
(2)において、\(\mu = 0, \sigma^{2} = 1\)となるものを標準ブラウン運動という。
\begin{eqnarray}
Z_{k}
&=& B_{\Delta k} - B_{\Delta k-1} \\
&\sim& N(\mu \Delta k, \sigma^{2} \Delta k) - N(\mu\Delta(k-1), \sigma^{2}\Delta(k-1)) \\
&\sim& N(\mu \Delta(k-(k-1)), \sigma^{2} \Delta(k-(k-1))) \\
&\sim& N(\mu\Delta, \sigma^{2}\Delta) \\
\end{eqnarray}
これは、正規分布となる確率変数
\(f(z_{k}) = \displaystyle \frac{1}{\sqrt{2\pi}\sigma^{2}\Delta} \exp\Bigr\{ - \frac{(z_{k}-\mu\Delta)^{2}}{2\sigma^{2}\Delta} \Bigr\}\)
この\(\delta\)が0に近づいていけば、どんどんこの感覚は狭くなっていくので、よりパスが滑らかなものになっていきます。
この時パスが今回は確率変数になり、
定義をよりイメージ的に
上の定義、ちょっとわからないですよね。。
なので、図を使って噛み砕いてみましょう!
ちょっとここで、上の定義
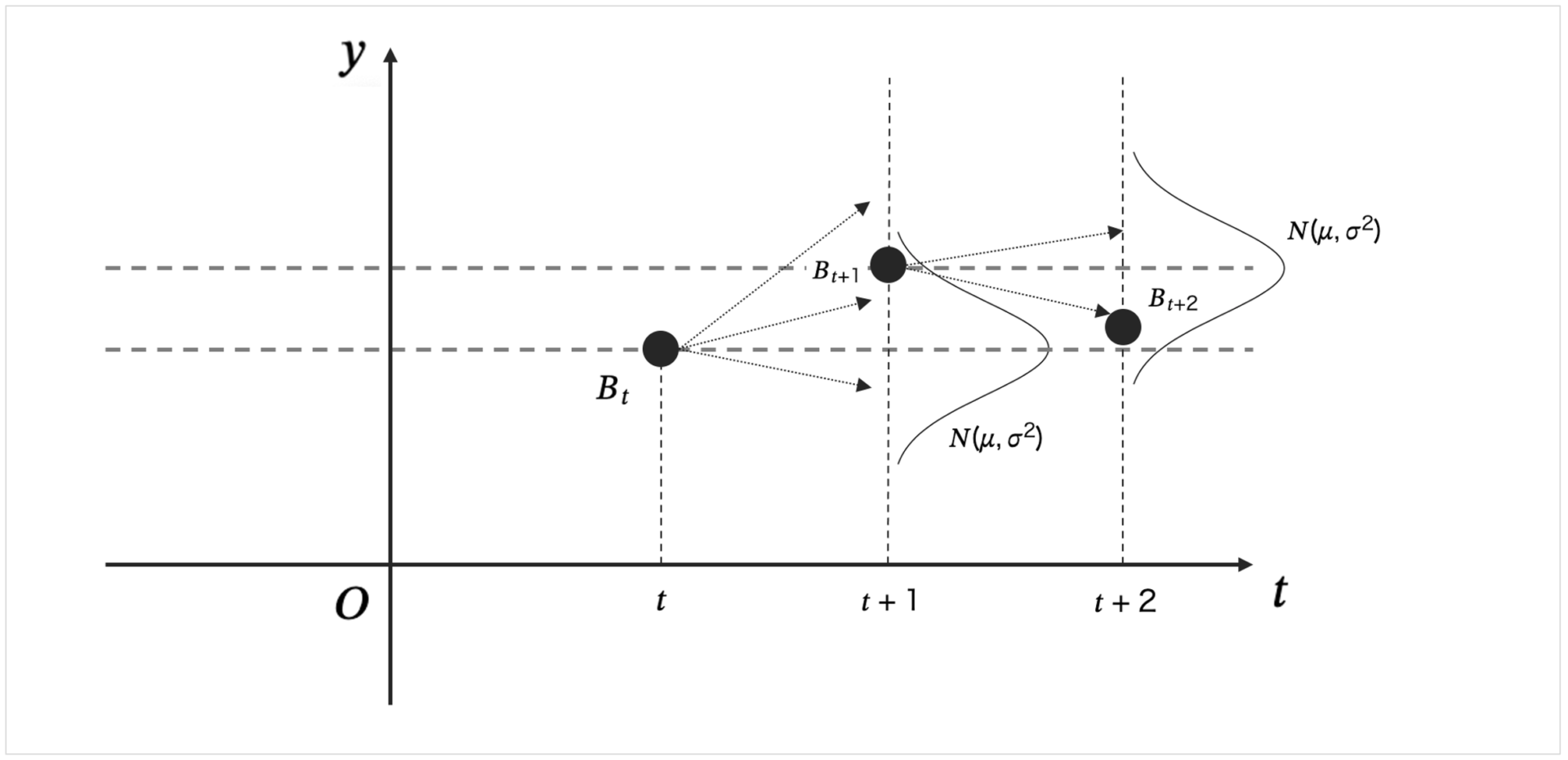
各点にて、\(N(\mu t, \sigma^{2}t)\)で次のt+1時点の値がサンプリングされます。
つまり各t時点において、正規分布によって遷移していくのがブラウン運動になり、その正規分布が標準正規分布である場合、標準ブラウン運動ということになります。
(通常正規分布は上に凸のグラフで見てるので、ちょっと違和感があると思いますが、このように横にどんどんデータが繋がっていきます。)
各点からは、\(N(\mu, \sigma^{2})\)で次の点のサンプリングが行われます。(行われるというか想定)
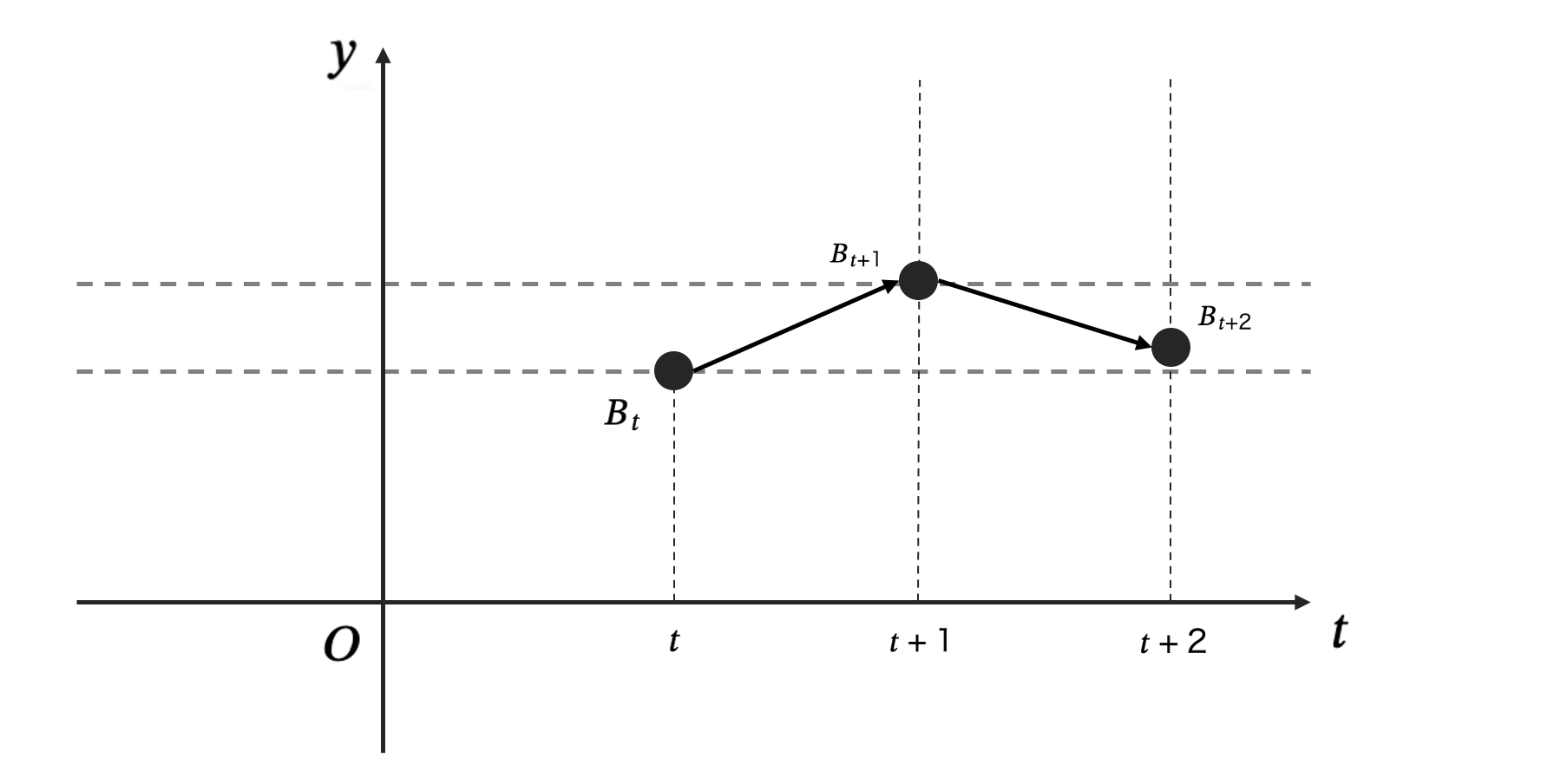
例として、t時点からt+1時点へのパスは、
\begin{eqnarray}
Z_{t}
&=& B_{t+1}-B_{t} \\
&\sim& N(\mu(t+1), \sigma^{2}(t+1)) - N(\mu t, \sigma^{2}t) \\
&\sim& N(\mu((t+1)-t), \sigma^{2}((t+1)-t)) \\
&\sim& N(\mu, \sigma^{2}) \\
\end{eqnarray}
となり、各\(t\)時点において、\(N(\mu, \sigma^{2})\)によってサンプリングされるということになります。
まず、\(t\)時において\(t+1\)時の値を平均として\(N(\mu, \sigma^{2})\)でサンプリングし、\(t+1\)期の値の\(B_{t+1}\)を取得します。
次に\(B_{t+1}\)の値を平均と見て、\(N(\mu, \sigma^{2})\)で\(t+2\)期の値の\(B_{t+2}\)を取得します。
このようにして繰り返しサンプリングをして今の時系列データが生成されるというメカニズムを仮定しています。
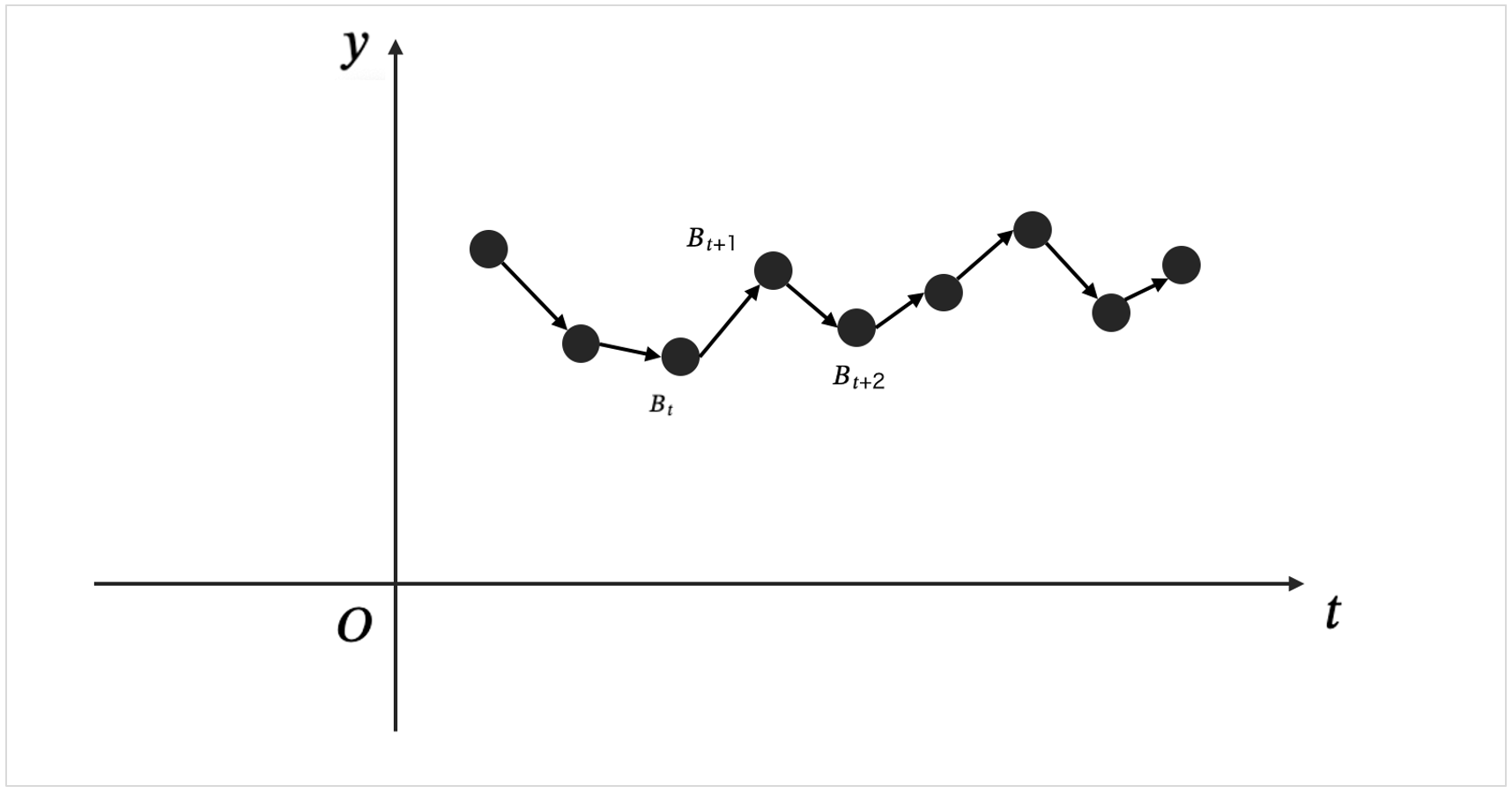
そして取れたデータを繋いでいくと以下のようにパスが出来上がります。これが運動で、今回のブラウン運動では確率変数になります。
このパスが確率変数になるということは、確率変数があるので確率密度関数を持つということにもなります。
そうすると、この確率変数が取る分布を考えて、どんな関数になるのか、パラメータを求める必要があります。
となると、どうやってパラメータを求めるのか。。
そうです!確率密度関数のパラメータを求めるには、点推定である「最尤法」を用います!
最尤法については、以下にて扱っているのでぜひご覧ください!
より\(\delta\)を0に近づけていけば、より細かな間隔でのパスを作ることができます。
最尤法によるパラメータ推定
よって、尤度は、
\begin{eqnarray}
L
&=& f(z_{1}) \cdot f(z_{2}) \cdot f(z_{3}) \cdot \cdot \cdot f(z_{n}) \\
&=& f(z_{1}) \cdot f(z_{2}) \cdot f(z_{3}) \cdot \cdot \cdot f(z_{n}) \\
\end{eqnarray}
\begin{eqnarray}
L
&=& f(z_{1}) \cdot f(z_{2}) \cdot f(z_{3}) \cdot \cdot \cdot f(z_{n}) \\
&=& f(z_{1}) \cdot f(z_{2}) \cdot f(z_{3}) \cdot \cdot \cdot f(z_{n}) \\
\end{eqnarray}