信頼区間とは、、、
よくある間違いとして、95%の確率で真の平均がこの区間に含まれるということではありません。
最終的に求める区間は
\begin{eqnarray}
P(10 < \mu < 15 ) = 0.95
\end{eqnarray}
の形で、確かに\(\mu\)が10から15の間に95%の確率で真の平均が入っているということに読み取れると思います。
この式だけを見ると、そう感じてしまうかもしれないです。
ただ一回計算過程を振り返ってみます。
いくつか確率変数が取れました。
それらのデータから今回の信頼区間を出しました。
\(\mu\)も確率変数で、取れたデータによってこの信頼区間が変わることは容易に想像できると思います。
ということは上の結果が必ず、常に出されるわけではないということがわかると思います。
となるとこの信頼区間を何個も出していき、100回出してみます。
100回出したうち、95パーセントつまり、95回ほど重なっているものが真の平均に近いということになります。
サンプルで採れたデータに対して信頼区間を構築した時、95%の確率でその区間の中に母平均が入っていると考えると、
滅多に出ないような外れ値のデータが例えば20回サンプリングした時18回くらい出たとします。
そのデータに対して母平均を出すとほぼ母平均の信頼区間は外れ値レベルの母平均になる可能性があります。
となると、この区間の中に95%の確率で母平均が入るとは考えにくいです。
なので、いきなりデータに対していきなり区間を構築して、その区間の中にほぼほぼ母平均が入っていると考えることはおかしいことなのです。
信頼区間を出すには、どのようにすればいいか。
さまざまな確率密度関数はパラメータの値が変わることで、分布の形は代わり、そして確率変数の確率も変わります。
そうなった場合、最後判断する5%確率となる確率変数点は毎回データを取るたびに変わってしまい、信頼区間を求めるのは難しくなります。
そのため、信頼区間を出すためには、中心極限定理を用います。
そうすることで、データ量が増えれば増えるほど、分布は標準正規分布\(N(0,1)\)に収束していき、\(y\)軸対象な確率分布になります。
これによって、正規分布と二項分布については\(n->∞\)で標準正規分布になります。
この性質を用いて信頼区間を求めてみましょう!
パラメーを求める方法として、以下2つがあります。
- 点推定
- 区間推定
点推定はもうパラメータの値を特定する、つまり1点になるということ、区間推定はおおよそこのパラメータはこの区間の中の値を取るであろうと推測するように区間を推定するものです。
その区間推定の1つの手法である、信頼区間について考えていきましょう。
Contents
信頼区間の考え方
正規分布や二項分布はそれぞれの分布で確率変数の形式は違います。
正規分布ではそのまま採れたデータが確率変数になりますが、二項分布では複数回実行してその0,1の和が確率変数の値になり、つまりはn回やってやっと1つの確率変数の値が取れるということです。
分布によって確率変数の定義が違うのは注意です。
そして、普通の上記の分布ではy軸対象ではなく、さらにはパラメータによってはかなり形が変わってしまう。
そこで、正規分布や二項分布については、n->∞で標準正規分布に収束するという性質を使って、信頼区間を構成することができます。
必ず標準正規分布に収束し、さらにはy軸対象の分布になるので、標準正規分布用の確率変数に正規分布と二項分布の確率変数から変換をして、扱えるようにする必要があります。
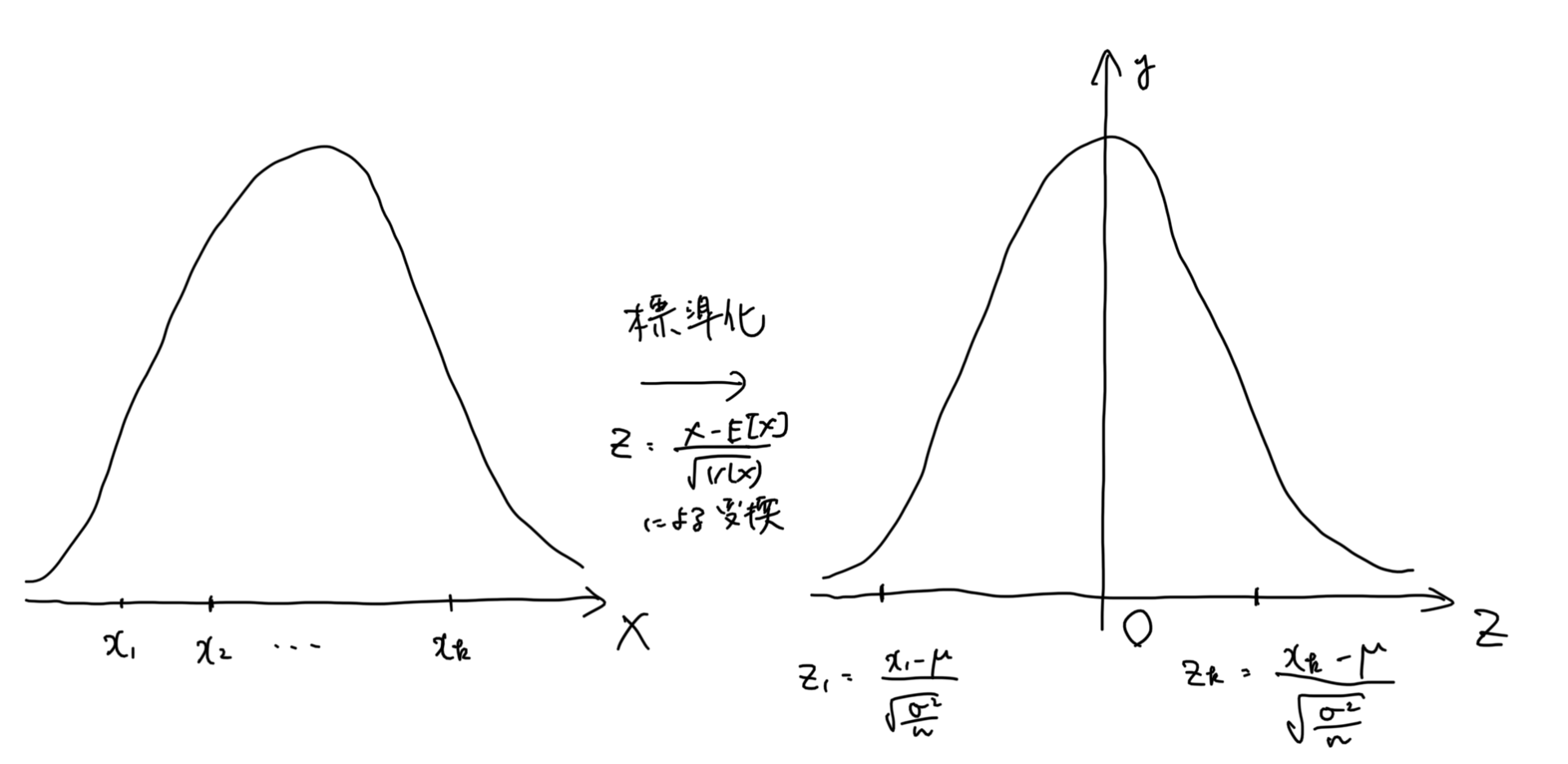
ここで採れたデータを、右の標準正規分布の確率変数に対応させます。
これによって、以下のように標準正規分布ではy軸対象でかつ確率が求まっているので(パラメータがないので形も変わらず確率が固定なので)、出したい信頼区間の範囲を求めることができます。
そのため、右の\(\displaystyle Z=\frac{X-E[X]}{\sqrt{V(X)}}\)に変換をした場合は、以下のように区間を考えることができます。
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < Z < z_{\frac{\alpha}{2}}) &=& 1-\alpha ・・・①
\end{eqnarray}
【連続】正規分布の平均\(\mu\)の信頼区間
1つの確率変数でヒストリグラムや確率密度関数を想像しながら、信頼区間を構成します。
母分散は経験やデータからすでにわかっているが、母平均はまだ不明な状況を仮定して、母平均の信頼区間を推定してみたいと思います。
ここでは母分散はすでにわかってるので定数で\(\sigma^{2}\)(0より大きい)とし、母平均はわかっていないのでひとまず
ここで母分散や母平均はまさにそれぞれの標本データの分散の期待値、平均の期待値であり、n->∞です。
中心極限定理もn->∞の話なので、
ここではデータが十分ある前提の話として考えることで、以下のような等式が完成します。(左辺も無限大。母平均、母分散を使っていて、右辺は標準正規分布の確率)
標準正規分布を使用するので、出だしは標本平均を確率変数とみなして考えていきます。
標本平均\(\bar{X}\)の期待値\(E[\bar{X}]\)は、\(\hat{\mu}\)で、
標本平均\(\bar{X}\)の分散\(V(\bar{X})\)は、\(\displaystyle\frac{\sigma^{2}}{n}\)なので、
正規化すると、
\begin{eqnarray}
Z
&=& \frac{\bar{X}-E[\bar{X}]}{\sqrt{V(\bar{X})}} \\
&=& \frac{\bar{X}-\hat{\mu}}{\sqrt{\frac{\sigma^{2}}{n}}} \\
\end{eqnarray}
となります。
両側推定で有意水準5%とすると、両端に5%と5%になるのでその間の確率は0.9になり、①から、
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < \frac{\bar{X}-\hat{\mu}}{ \sqrt{\frac{\sigma^{2}}{n}}} < z_{\frac{\alpha}{2}}) &=& 0.9
\end{eqnarray}
と表せます。
左辺を展開していきましょう。
\(\displaystyle\frac{\sigma^{2}}{n}\)は0より大きいので、分母を払い、そして\(\hat{\mu}\)について解くと、
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < \frac{\bar{X}-\hat{\mu}}{ \sqrt{\frac{\sigma^{2}}{n}}} < z_{\frac{\alpha}{2}})
&=& P(-z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}} < \bar{X}-\hat{\mu} < z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}} ) \\
&=& P(-\bar{X} -z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}} < -\hat{\mu} < -\bar{X} + z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}} ) \\
&=& P(\bar{X} - z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}} < \hat{\mu} < \bar{X} + z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}} ) \\
\end{eqnarray}
よって、有意水準10%での、母分散がすでにわかっていて、母平均がわからない時の母平均\(\hat{\mu}\)の信頼区間は
\begin{eqnarray}
(\bar{X} - z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}}, \bar{X} + z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\sigma^{2}}{n}})
\end{eqnarray}
になります。
上の信頼区間をもう少し見てみましょう!
nを大きくすると点推定
信頼区間は当然ながら小さくしたいというのが通常である。
信頼区間を見ると両辺の分母にnがある。つまり、サンプルデータを増やしていけば0になり、
標本平均に収束していくことがわかる。
なのでデータが多ければ多いほど、点推定に近づくということになる。
(やっぱデータは多い方がいいってことね!)
【連続】正規分布の分散\(\sigma^{2}\)の信頼区間
1つの確率変数でヒストリグラムや確率密度関数を想像しながら、信頼区間を構成します。
今度は、母平均がわかっていて、母分散がわかっていない時に、母分散の信頼区間を構成してみたいと思います。
今回も標準正規分布を使用するので、出だしは標本平均を確率変数とみなして考えていきます。
標本平均\(\bar{X}\)の期待値\(E[\bar{X}]\)はわかっているので\(\mu\)で、
標本平均\(\bar{X}\)の分散\(V(\bar{X})\)は、未知なので\( \displaystyle\frac{\hat{\sigma^{2}}}{n} \)なので、
正規化して、両側推定で有意水準5%とすると、両端に5%と5%になるのでその間の確率は0.9になり、
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < \frac{\bar{X}-{\mu}}{ \sqrt{\frac{\hat{\sigma^{2}}}{n}}} < z_{\frac{\alpha}{2}}) &=& 0.9
\end{eqnarray}
と表せます。
左辺を展開していきましょう!
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < \frac{\bar{X}-{\mu}}{ \sqrt{\frac{\hat{\sigma^{2}}}{n}}} < z_{\frac{\alpha}{2}})
&=& P(-z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\hat{\sigma^{2}}}{n}} < \bar{X}-{\mu} < z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\hat{\sigma^{2}}}{n}} ) \\
&=& P(-z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\hat{\sigma^{2}}}{n}} < \bar{X}-{\mu} < z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{\hat{\sigma^{2}}}{n}} ) \\
\end{eqnarray}
このように正規分布の信頼区間は、中心極限定理を用いるためにはただの正規分布の確率変数ではダメで、別の確率変数である標本平均を用いることで、確率変数の和になり、
標準正規分布に\(n->∞\)で収束するという性質を用いて、信頼区間を構成しました。
信頼区間とは未知である母分散の推定区間を求めるものです。
そしてその区間は標本データから算出します。
となると、母分散は標本データから算出しようとすると期待値は過小評価してしまうため、単純に上記のようにおいて計算するとずれることになります。
そのため、ここでは単純に未知と仮定するだけではなく、不偏分散を用いて計算をするようにします。
不偏分散\(s\)として、\(\displaystyle \frac{\bar{X}-\mu}{\displaystyle \sqrt{\frac{s^{2}}{n}}}\)とします。
そしてこれを
\begin{eqnarray}
t &=& \frac{\bar{X}-\mu}{\sqrt{\frac{s^{2}}{n}}}
\end{eqnarray}
とすると、これはスチューデントの\(t\)分布と呼ばれるものになります。
ちなみに、今までは\(Z\)であったので標準正規分布の確率を用いて信頼区間を算出していましたが、\(t\)分布に従う変数に置き換えたので、
上記のtの式で算出する場合は、スチューデントの\(t\)分布の確率を用いて信頼区間を算出することになります。ちなみにこのスチューデントのt分布も標準正規分布と同じようにy軸対象な分布になります。
【離散】二項分布の確率\(p\)の信頼区間
1つの確率変数でヒストリグラムや確率密度関数を想像しながら、信頼区間を構成します。
1つの離散確率変数で信頼区間を構築する際に使用します。さらには二項分布なので、2つの種類に分けた上で信頼区間を考えます。
1つの変数が2つの値しか取らない場合、二項分布ではなく、6つとったとしてもそれを2つの種類、例えばサイコロで1,2と3,4,5,6の2つに分けるなどでも二項分布を適用することができます。
二項分布の確率がデータから解らないとして、この確率\(p\)( \(p > 0\)とする)の信頼区間を構成してみましょう。
正規分布の場合では、確率変数をXとしたら、標本平均を定義することで、
確率変数の和で表現できたので、それによって中心極限定理によって最終的に標準正規分布に帰着して算出することができました。
じゃあ、二項分布も標本平均を出すのか?というとそうではなくて、
二項分布の確率変数はすでに和で表現されているので、基本的にはそれを用いることで簡単に中心極限定理を使用することができます。
ここで二項分布の確率変数を\(S_{n}\)とすると、
\(S_{n}\)の期待値は\(np\)、分散は\(np(1-p)\)になるので、
信頼区間は、
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < \frac{S_{n}-np}{\sqrt{np(1-p)}} < z_{\frac{\alpha}{2}}) &=& 0.9
\end{eqnarray}
と表せます。
左辺を展開していきましょう!分散は0より大きいので、
\begin{eqnarray}
P(-z_{\frac{\alpha}{2}} < \frac{S_{n}-np}{\sqrt{np(1-p)}} < z_{\frac{\alpha}{2}})
&=& P(-z_{\frac{\alpha}{2}}\sqrt{np(1-p)} < {S_{n}-np} < z_{\frac{\alpha}{2}}\sqrt{np(1-p)}) \\
\end{eqnarray}
\(p\)の信頼区間を求めるため、上記の不等式を\(p\)について解く必要があるので、二次不等式を解きましょう。