ロジスティック回帰分析は、その名の通りロジスティックな回帰分析です。
はい。意味わかんないですね。
ロジスティック回帰分析というと、統計学初学者は何のことがわからず挫折することが多いかと思います。
そしてとりあえず検索して調べたり、参考書などを買って読んでも数式の羅列ばっかりでより挫折して、
そのまま投げやりになってしまう方も多いと思います。
ここでは、そんな数式ばっかで理解するのが難しいロジスティック回帰分析について話していきたいと思います!
Contents
ロジスティック回帰分析とは
回帰分析という言葉があるので、
なんとなく以下の式を想像するかと思います。以下は
- 単回帰分析 \(y=\beta_{0} + \beta_{1}x_{1}\)
- 重回帰分析 \(y=\beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2}\)
- 非線形回帰分析 \(y=\beta_{0} + \beta_{1}x + \beta_{2}x^{2}\)
ですね。
回帰分析はxの値が取れた時、yの値を予測するというのが回帰分析です。
まず回帰分析はこれでOKです。
で、問題はロジスティックという言葉なのですが、
回帰分析の\(y\)(推測したい目的のものなので、目的変数)の取り得る値はマイナス無限から無限大。
\(x\)(説明変数)の値によって\(y\)の値の予測をします。
しかし、\(x\)の値を使って確率を出したい場合があります。
このような説明変数があるとき、購入する確率であったり。
回帰分析ではこのような説明変数があるとき、目的変数はどのくらいの値になるのかを予測しますが、
ロジスティック回帰ではこのような説明変数があるとき、どのくらいの確率で発生するかを予測します。
つまり\(y\)が目的変数になるので、0から1を取るものです。
取れた\(x\)の値から、いや0と1の間になる\(y\)なんて難しいんじゃないの?と思った方、ほんとその通りです!
でも、うまく計算をすることで、\(x\)の値が例えば1000000だったとしても、-9876でも0から1に絞れます。
以下の関数を用いることでそれが可能になります。
ココがポイント
回帰分析は予測値を求めるもの、ロジスティック回帰分析は確率を求めるもの。
ロジスティック回帰分析に使用する関数
ロジスティック回帰分析では、上で説明したように0から1に変換する関数を用いる必要があります。
二次関数\(y=x^{2}\)は、どんな\(x\)の値でも二次関数は\(y\)の値を0以上に変換します。
これは、どんな\(x\)の値でも0から1に変換する関数ではないですね。。
ではどんな関数が0から1に変換をするのでしょうか。その関数は「シグモイド関数」と呼ばれ以下の式で表されます。
シグモイド関数
\begin{eqnarray}
y=\frac{1}{1+e^{-x}}
\end{eqnarray}
上記のシグモイド関数に対して右辺の分子分母に\(e^{x}\)をかけて、
\begin{eqnarray}
y=\frac{e^{x}}{1+e^{x}}
\end{eqnarray}
と書いてあるものもあったりします。
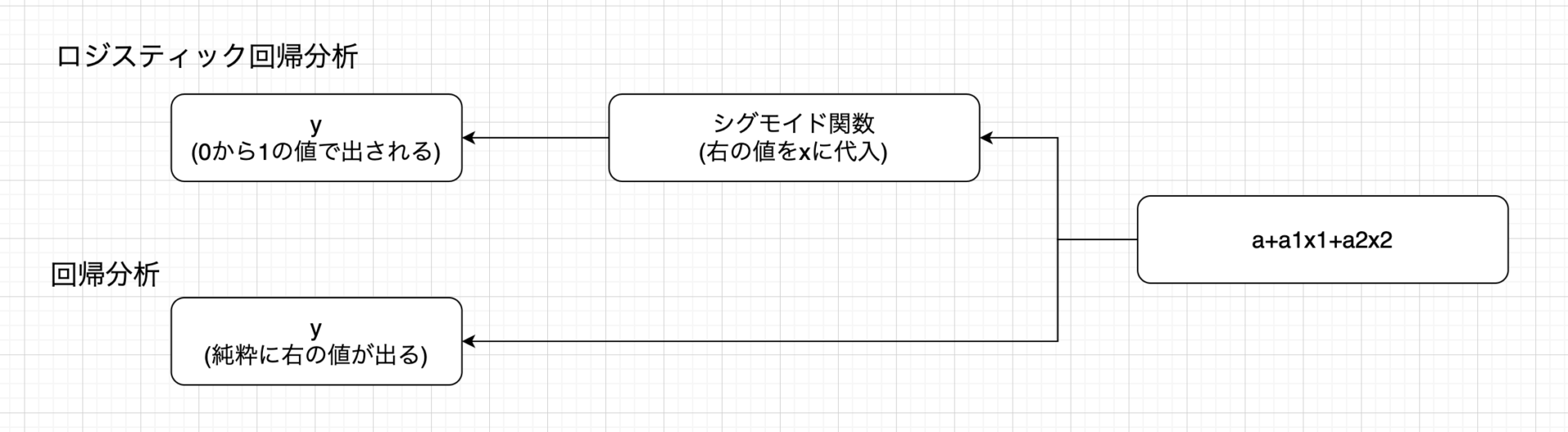
シグモイド関数の\(x\)と書いてある部分がいわゆる\(x\)の式で、つまり説明変数の式になります。
単回帰であれば、\(x\)の部分を\(ax+\epsilon \)というように置き換えたり、
重回帰であれば、\(x\)の部分を\(a_{1}x_{1} + a_{2}x_{2} + \epsilon \)というように置き換えたりして、ロジスティック回帰分析を行います。
シグモイド関数の図示
で、シグモイド関数というのを用いるとはわかったけど、実際それはどんな曲線を描く関数なのか?
実際ここで図示してみようと思いますが、実はこの関数を見るとちょっと面白かったりします!
関数を実際に見てみることで、ロジスティック回帰の理解もできるようになると思います。
数学に馴染みのない方からするとこんな形の関数があるんだってびっくりされることがちょくちょくあったので。。
\(y=f(x)\)とすると、線形代数での表現である写像や、実数の集合\(\mathbb{R}\)、そして0より大きく1より小さいを集合で表す\((0,1)\)を用いて、
以下のように表現されます。
シグモイド関数は、実数をとるどんな\(x\)の値も、この関数を通すことによって、\((0,1)\)の値に変換される。つまり確率に変換するということです。
\begin{array}{rccc}
f\colon & \mathbb{R} &\longrightarrow& (0,1) \\
& x & \longmapsto & f(x)
\end{array}
シグモイド関数はAIやディープラーニングなどでも使用される関数です。この関数を用いることで、どんな値でも0から1の値に絞り込むことが可能になります。
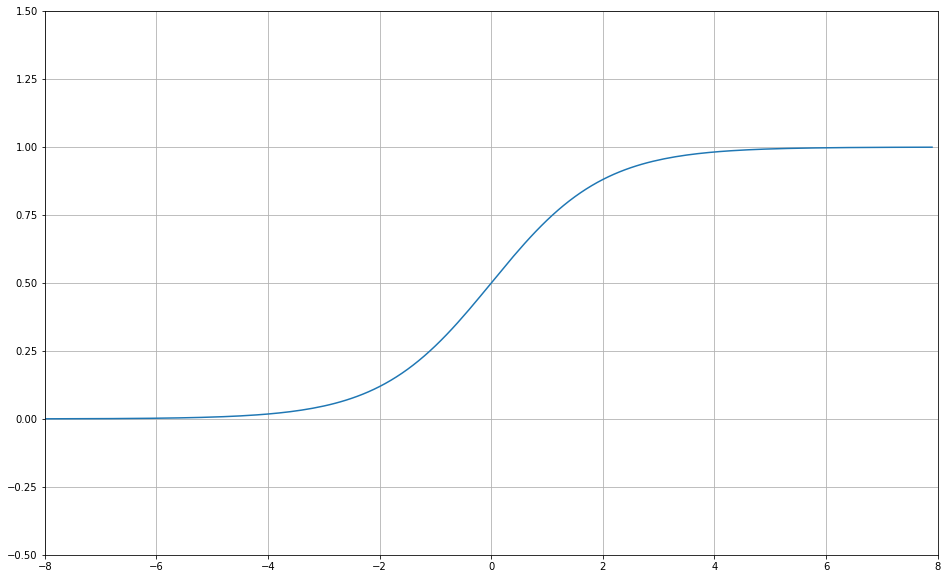
実際にグラフ化してみましょう!
import numpy as np import matplotlib.pyplot as plt # xの値(-8~8で0.1刻みで配列生成) x = np.arange(-8, 8, 0.1) # シグモイド関数 y = 1 / (1 + np.exp(-x) ) # グラフの設定 fig = plt.figure(figsize=(16,10)) plt.plot(x, y) # プロット plt.xlim(-8, 8) # x軸の範囲 plt.ylim(-0.5, 1.5) # y軸の範囲 plt.grid() # グリッド描画 plt.show() # グラフを出力
上記がシグモイド関数になります。区間的には\(-8 \le x \le 8 \)だが、\(y\)は\(0 < y < 1\)の中に収まっています。
このようにどんな\(x\)の値でも\(0 < y < 1\)に変換するのがシグモイド関数の特性です。
\(e^{x}\)からこの値は常に0より大きいため、この関数は確かにyのとる値は0から1です。
xを-100000とかしてみると、0には限りなく近い値にはなりますが、どんなにxが小さい値でも\(e^{x}\)は0にはなりません。もし\(e^{x}\)を0とすると、yは1になるので、1にも限りなく近くはなるが1にはなりません。
xの値をyに変換する、落とし込むというのが写像という概念です。
今回で言うと、xは回帰分析の右辺に値します。その値をyに変換する。そしてシグモイド関数は0から1に落とし込む関数なので、まさに確率
ロジスティック回帰分析の右辺の式について、
データが取れた時、回帰分析だと実測値の予測をしていたが、そのデータが出る確率を求めるのがロジスティック回帰分析になります。
そしてシグモイド関数それ自体、確率の意味を持つのでいわゆる二項分布の確率だったりにそのまま適用することができます。
ロジスティック回帰分析でパラメータを求める
これによって、確率をある基準で、
2つに分けることができました。
2つに分けたということは、二項分布を考えることができます。
二項分布は2つの
二項分布
あるxというデータが取れた時、そのデータを成功なのか、失敗なのかに振り分けます。
そうすることで、まさに二項分布になります。
毎回xのデータのサンプリングが取れた時、それが成功なら1、失敗なら0というように振り分けを考えれば、
まさに成功の確率をpとした時、失敗は1-pでこれは二項分布になります。
そして今ロジスティック回帰分析によって、あるxが取れた時、その確率を求めるわけですが、
まさにそれが成功なら成功確率が、失敗なら失敗確率が出るわけです。
まだこの時確率自体はスカラー値は出せず、パラメータが含まれている状態での確率式になります。
この状態で、二項分布を考え、
二項分布で最尤法でパラメータを求めることになります。
フィッシャースコア法
先程二項分布で最尤法を用いてパラメータを求めようとしましたが、実際には計算が難しく求めることができません。
そこで、フィッシャースコア法を用います。
この式について簡単に説明すると以下のような原理です。
数2で学んだことはあるかと思います!
接線方向でx軸と交わっていく方法です。
2次関数の最小値は下に凸(下に突起がある)の場合は最小値が存在しますが、平方完成を用いれば一発で出ますが、
フィッシャースコア法を用いることで段々と収束していき、その最小値となるxを求めます。
(ちなみに下に凸では接線の傾きは\(f'(x)=0\)なので、それで求めることもできます。
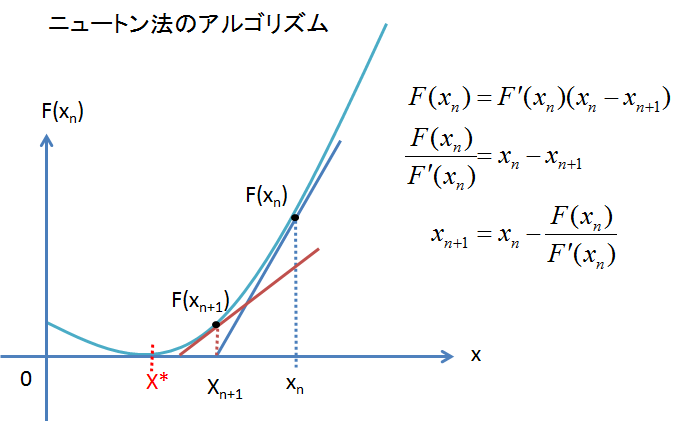
ニュートン法(ニュートンラフソン法)
画像の参照URL:https://ameblo.jp/zrfcsctd/entry-11235319941.html
ある関数\(y=f(x)\)のある\(x=x_{n}\)での接線の方程式を求めると以下の式になります。
\begin{eqnarray}
y - f(x_{n}) &=& f'(x_{n})(x-x_{n}) \\
y &=& f'(x_{n})(x-x_{n}) + f(x_{n})
\end{eqnarray}
そして、この接線がx軸と交わった点を\(x_{n+1}\)とします。そうすると、上の式から、\(y=0, x=x_{n+1}\)より、
\begin{eqnarray}
0 &=& f'(x_{n})(x_{n+1}-x_{n}) + f(x_{n}) \\
-f'(x_{n})(x_{n+1}-x_{n}) &=& f(x_{n}) \\
x_{n+1}-x_{n} &=& - \frac{f(x_{n})}{f'(x_{n})} \\
x_{n}-x_{n+1} &=& \frac{f(x_{n})}{f'(x_{n})}・・・①
\end{eqnarray}
※ 傾き\(f'(x_{n+1}) = 0\)とする。
※ 傾き\(f'(x_{n}) \neq 0\)とする。
よって、\(x_{n+1}\)と\(x_{n}\)の漸化式が求まりました。
上のことを繰り返しやっていけば、①式の\(n\)を\(n+1\)に、\(n\)を\(n+2\)にしていけば、
\begin{eqnarray}
x_{n+1}-x_{n+2} &=& \frac{f(x_{n+1})}{f'(x_{n+1})} \\
x_{n+2}-x_{n+3} &=& \frac{f(x_{n+2})}{f'(x_{n+2})}
\end{eqnarray}
これを両辺を足せば、\(x_{n}とx_{∞}\)が残り、収束していきます。
このように、ニュートンラフソン法は=0と置いて、瞬時に求めるのではなく、
勾配降下法を用いて、徐々に求めたい値を収束して求めていく方法になります。
よってこの式は\(f(x)=0\)を満たす\(x\)を求めるための漸化式になります。
本題に戻ります
今求めたいものは、以下の式でした。
この式は左辺は微分されている状態の式で、最尤法なので微分した式=0となるので、右辺は0です。
これってまさに上のニュートンラフソン法です。
左辺の式は\(f(x)\)ではなく1回微分したものです。なので、上記①の式の右辺は左辺を1回微分したものなので、
右辺を2階微分したものに置き換えればいいわけです。
ということは上記の式は、以下の式で求めることができます。
\begin{eqnarray}
x_{n} - x_{n+1} &=& \frac{f'(x_{n})}{f''(x_{n})}・・・②
\end{eqnarray}
上で見た通り、この漸化式によって\(f(x)=0)\)を満たす\(x\)を求めていくことができます。
そして今回求めたい二項分布の最尤推定ですが、
最尤法の式は尤度でパラメータで微分した式=0です。
なので、\(f(x)=\)パラメータで微分した式とすると、\(f(x)=0\)となり、上のような式を満たします。
これによって、上では\(f(x)\)は微分してなかったが、今回の\(f(x)\)は1回既に微分しているので、
①式では右辺の分子は2回微分に、分母は3回微分になります。
※ ニュートン法では必ず収束するとは限りません。
二つの山があったりします。そういう場合、どちらかに収束する可能性があり、求めたいものがもとまる保証はない。
ロジスティック回帰分析をpythonで
クロスバリデーションを用いるデータについては、各自入れて分析をする。
# 【クロスバリデーション】訓練データ
train_x = train_df.drop(list_col,axis=1) # 説明変数
train_y = train_df['メンバー'] # 目的変数
# 【クロスバリデーション】本番データ
valid_x = valid_df.drop(list_col,axis=1) # 説明変数
valid_y = valid_df['メンバー'] # 目的変数
# 説明変数は標準化
scaler_X = StandardScaler()
train_x = scaler_X.fit_transform(train_x)
valid_x = scaler_X.transform(valid_x)
# モデル学習
model = LogisticRegression() # ロジスティック回帰のインスタンス
model.fit(train_x, train_y) # modelインスタンスに回帰係数などのプロパティ情報が入る
model.predict(valid_x) # 構築したモデルで本番データの説明変数で実行
model.score(valid_x,valid_y) # ロジスティック回帰分析の決定係数
# 分析結果
print("【標準偏回帰係数】", model.coef_)
print("【切片】", model.intercept_)
print("【決定係数 R^2 (訓練データ)】:", model.score(train_x, train_y))
print("【決定係数 R^2 (本番データ)】:", model.score(valid_x, valid_y))
print('【正解率】Accuracy={}'.format(model.score(valid_x,valid_y)))