生存時間解析には以下2つのパターンがあります。
・ハザード関数
・カプランマイヤー
ハザード関数は打ち切りデータを含む場合
カプランマイヤーは打ち切りデータを含まない場合
の分析を行う。
生存時間関数などを求めていくのですが、求めていく目的を考える必要があります。
関数を求めることで、パラメトリック検定など2つの群、例えば薬を投与した検体と薬を投与していない検定、それぞれの生きている確率などに差があるのかどうかを見るために、関数などを求めることで、検定につなげようというのが目的になります。
ここではそんな生存関数などを求めることについて説明していこうと思います。
ハザード関数
このハザード関数はいろんな分野で扱われるが、関数名などが結構寿命を取り扱うような名称(ハザード関数とか生存関数とか)になっているので、
ここでいうイベントは生死に関わるようなイベントで考えていくのがいいです。
イベントが発生する時間をTとした時、
最初観察が開始した時では確率はほぼ0であるが、だんたんと時間が経っていくと確率は上がっていく。
なので、累積分布関数を用いて、以下のように表せる。
イベントが起きるまでの確率が上なので、逆の関数は生存関数で、余事象によって1から引いた値が生存関数となります。
なのでハザードなので、火事などのイベントもまさにこれと同じで、
さらには待ち時間を考える指数関数とも関わりがかなりあります。(指数関数も1回起きるまでの確率分布でもあったりする)
待ち時間の指数分布は、必ず起きることではない事象であり、
今回の場合は寿命というランダム性のあるものではなく、年々死ぬ確率が上がっていくような分布だからハザード関数という別の概念が必要になります。
寿命、すなわち時刻0に誕生した人が死亡する時刻は,確率変数であり、これを\(T\)で表します。
\(T\)を被験者の生存時間を表す確率変数とする。
登場関数
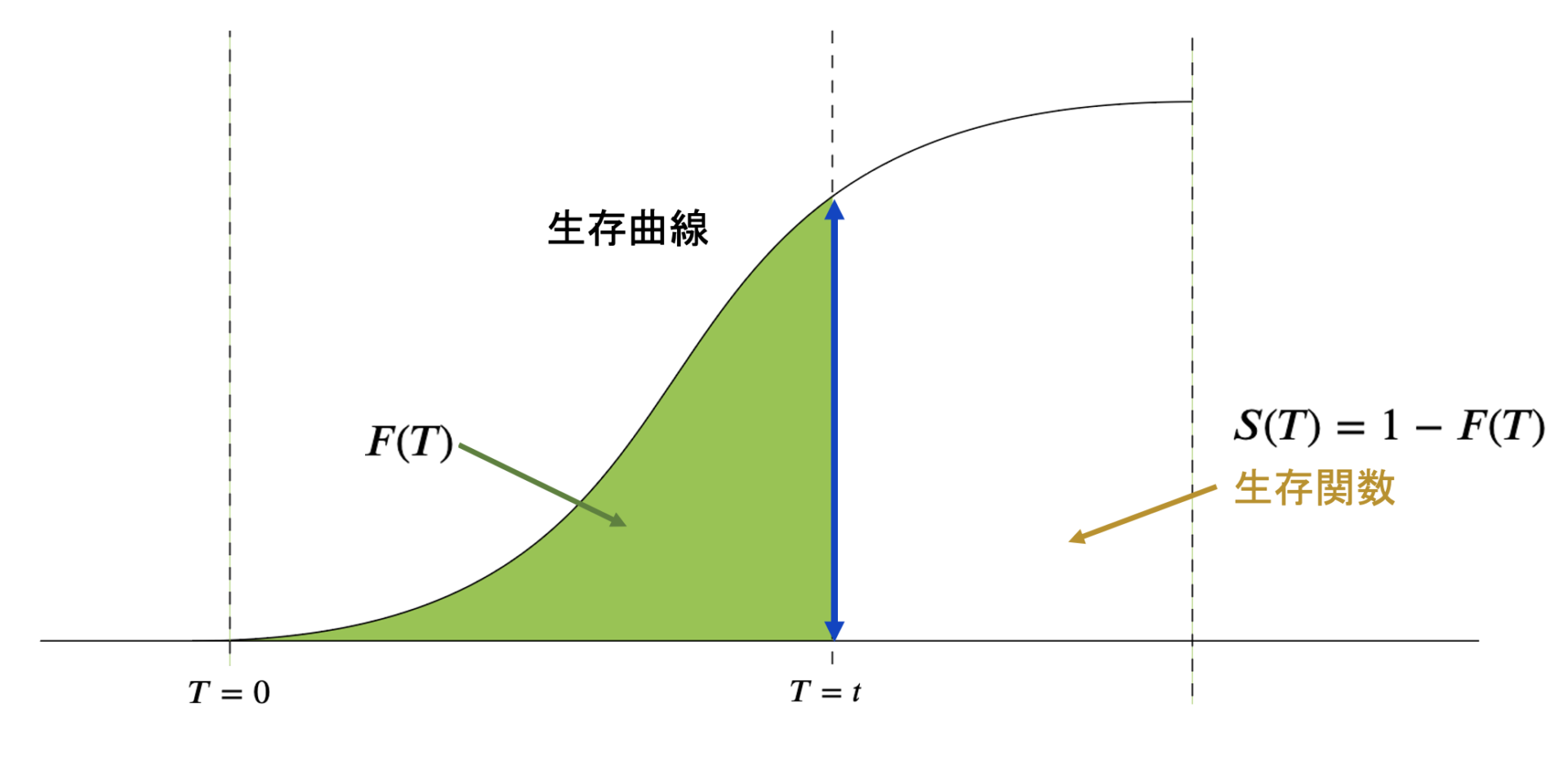
- 累積分布関数:\(F(T) = P(T < t) = \displaystyle \int_{0}^{t}f(t)du \)、いわゆるある時点\(t\)まででイベントが起きる確率( \(T < t\)で\(t\)前までの\(T\)つまりイベント:寿命が尽きるので、その\(t\)までにイベントが起きる確率、つまりイベントが起きる確率)
- 確率密度関数:\(f(T) = - \displaystyle \frac{d}{dt}S(T) \)、いわゆる\(T\)時点になくなる確率(イベントが起きる確率)
- 生存関数:\(S(T) = 1 - F(T)\)、余事象なので、イベントが起きない確率、つまり生存している確率
- ハザード関数:\(h(T) = \displaystyle \frac{f(T)}{S(T)}\)、この式よく見ると、\(f(T)\):T時点でのイベントが起きる確率、\(S(T)\):T時点でのイベントが起きない確率、これってオッズ比に見えますね!そうです!オッズ比で起きる確率/起きない確率ということになります。このオッズ比のことをハザード比と言います。被験者が時点tまで生存したという条件のもとで、その時間に死亡する確率です。
| 項目 | 式 | 説明 |
|---|---|---|
| 確率密度関数 | \(f(T) = - \displaystyle \frac{d}{dt}S(T) \) | いわゆる\(T\)時点になくなる確率(イベントが起きる確率) |
| 累積分布関数 |
\begin{eqnarray} F(T) &=& P(T < t) \\ &=& \int_{0}^{t}f(t)du \end{eqnarray} |
いわゆるある時点\(t\)まででイベントが起きる確率( \(T < t\)で\(t\)前までの\(T\)つまりイベント:寿命が尽きるので、その\(t\)までにイベントが起きる確率、つまりイベントが起きる確率)。\(f(t)\)がいわゆる\(T=t\)でのイベントが起きる確率なので、\(f(t_{i})\),\(f(t_{j})\)は互いに排反なので和による計算 |
| 生存関数 | \(S(T) = 1 - F(T)\) | 余事象なので、イベントが起きない確率、つまり生存している確率 |
| ハザード関数 | \(h(T) = \displaystyle \frac{f(T)}{S(T)}\) | この式よく見ると、\(f(T)\):\(T\)時点でのイベントが起きる確率、\(S(T)\):\(T\)時点でのイベントが起きない確率、これってオッズ比に見えますね!そうです!オッズ比で起きる確率/起きない確率ということになります。このオッズ比のことをハザード比と言います。 |
考え方
人は生きると死ぬの2つがあります。
その中で、死ぬというイベントは人生で1回きりで死ぬイベントが発生した場合、それ以降はもうイベントは発生しません。
まずこの生きる、死ぬを確率密度関数で置いてみます。
確率密度関数\(f(t)\)を時点\(T=t\)で死ぬ確率であり、これは原点を通る右肩あがりの関数です。
\(t=0\)では生まれた瞬間です。出産時に何かで死ぬことはあるかと思いますが、一旦は考えず、普通は確率はほぼ0に近いです。つまり一応\(f(0) = 0\)と言えそうです。
続いて、確率密度関数\(s(t)\)を時点\(T=t\)で生きる確率であり、これは原点を通る右肩下がりの関数です。
\(t=0\)では生まれた瞬間です。出産時はもちろん生きているかと思います。ただ何かで死んでしまう可能性もありますが、一旦は考えず、普通は確率はほぼ1に近いです。つまり一応\(s(0) = 1\)と言えそうです。
生きていることと死んでいることは排反な関係なので、\(s(t) + f(t) = 1\)であり、それぞれの累積関数\(S(t)+F(t) = 1\)も成立します。
そして、余事象の関係で生きてる確率 + 死ぬ確率 = 1なので、\(F(T) + S(T) = 1\)となり、\(S(T) = 1 - F(T)\)と言え、これに対して\(t\)で微分することで、
\begin{eqnarray}
\frac{d}{dt}F(T) &=& - \frac{d}{dt}S(T) \\
f(t) &=& - \frac{d}{dt}S(T)
\end{eqnarray}
このようにストーリーで覚えていくと分かりやすそうです!
\begin{eqnarray}
h(T)
&=& \lim_{\delta(t) \rightarrow 0} {\frac{P(t < T < t+\delta(t) | T > t)}{\delta(t)}}
\end{eqnarray}
この定義式の意味するところは、
デルタを置いてそこを0にしていきます。そうするとだんたんと幅を狭めていくことができ、最終的には傾きを表す微分式になることが想像できます。
そして仮定として、条件付き確率を置いていて、それまでは全くイベントが発生していないという条件をつけた上で、その後で\(\delta(t)\)を0に縮めていくことで、瞬間的な確率を求めようとしています。
被験者が時点tまで生存したという条件のもとで、その時間に死亡する確率です。
tまで
もし条件付きがない場合は、それまでに1回も発生していない場合に加えて、イベントが1回発生しているだけではなく何回か発生している場合も含むなど、今回のハザード関数を考える上で破綻してしまいます。
そのため、今回条件付き確率として、それまで1回もイベントが発生していないという条件をつけて考えています。
\(T < t\)ならば、\(t\)がいわゆる起点で、それよりも前にイベントが発生しているという意味。
\(T > t\)なので、\(t\)でもまだ発生はしていなく、それ以降に発生するという意味になります。
なのでこの条件の元でを考え、起点\(t\)ではまだ発生していないよと仮定します。
そしてこの\(t\)(この年齢)になったときに、瞬間的にリスクの確率を求めます。イメージとしてはこの年になくなる確率的な意味合いですかね。
なので、ちょっと\(t\)にちょっとの時間経過を\(\delta(t)\)と表現してプラスすることで、\(t+\delta(t)\)で現在の時間tからちょっと時間が経ったときを考えます。
そしてその間で\(t < T < t+\delta(t)\)とすることで、この間でイベントが発生すると仮定しています。
そして最後に0に近づけることで、間接的にtに近づけていき、より瞬間的なリスク確率を出そうという仕組みです。
この式を計算していきましょう!
道なりに進んでいけば簡単に計算ができます。
途中で、共通部分があるが、\(P(t < T < t+\delta(t)) \cap P(T > t) = P(t < T < t+\delta(t))\)になることに注意して、
\begin{eqnarray}
h(X)
&=& \lim_{\delta(t) \rightarrow 0} {\frac{P(t < T < t+\delta(t) | T > t)}{\delta(t)}} \\
&=& \lim_{\delta(t) \rightarrow 0} {\frac{P(t < T < t+\delta(t)) \cap P(T > t)}{P(T > t)}} {\frac{1}{\delta(t)}} \\
&=& \lim_{\delta(t) \rightarrow 0} {\frac{P(t < T < t+\delta(t))}{\delta(t)}} {\frac{1}{P(T > t)}} \\
&=& \lim_{\delta(t) \rightarrow 0} {\frac{S(t) - S(t+\delta(t)) }{\delta(t)}} {\frac{1}{P(T > t)}}・・・① \\
\end{eqnarray}
※ \(S(t) = 1- P(T < t)\)を用いている。
そして微分の定義式で以下を用います。要は\(t\)時点での変化率を計算していて、だんたんと\(t\)に近づけていく
f(x)
&=& \lim_{t \rightarrow a} { \frac{f(t) - f(a) }{t-a} } \\
&=& \lim_{\delta(t) \rightarrow 0} { \frac{f(t+\delta(t)) - f(t) }{t+\delta(t) - t} } \\
&=& \lim_{\delta(t) \rightarrow 0} { \frac{f(t+\delta(t)) - f(t) }{\delta(t)} } \\
\end{eqnarray}
よって①から
\begin{eqnarray}
h(X)
&=& \lim_{\delta(t) \rightarrow 0} {\frac{S(t) - S(t+\delta(t)) }{\delta(t)}} {\frac{1}{P(T > t)}}・・・① \\
&=& -\frac{d}{dt}S(t) \cdot {\frac{1}{S(t)}} \\
&=& -{\frac{1}{S(t)}} \frac{d}{dt}S(t) \\
&=& -\frac{d}{dt}\log(S(t)) \\
\end{eqnarray}
となります。
ここまでに出てきた関数を一回整理しましょう!
累積分布関数:\(F(X)\)
確率密度関数:\(f(X) = - \displaystyle \frac{d}{dx}S(X) \)
生存関数:\(S(X) = 1 - F(X)\)
→ 生存関数とは生きている時間を意味します。死ぬというイベントが発生するまでの時間の確率はイメージですが、どんどん確率は高くなっていくと思います。
ハザード関数:\(h(X) = \displaystyle \frac{f(X)}{S(X)}\)

生まれた瞬間がいわゆる\(T=0\)であり、当然この時生存確率\(S(T) = 1\)である。
そこからどんどん生存確率\(S(T)\)は減少していく。
最初は\(F(T) =0\)で生まれたばかりなので確率は0であり、そこから徐々に死ぬ確率(イベントが発生する確率)が高くなっていく。
\(S(t) = f'(t)\)で、S(t)はf(t)の微分つまり傾き、つまり変化率に等しい。
生存関数やハザード関数をわかりやすく直感的に理解する
生存関数
直感的に生存関数を
生存関数は
0歳の時ほぼ亡くなることはないので生存確率はほぼ100%、
10歳の時に生きている確率は98%、
30歳では85%、
75歳では40%
としたとき、生きている確率は歳をとるにつれて低くなっていく。
なので生存関数は下降していく関数になります。
ハザード関数
ハザード関数とは、今までは生存していたけど、ある時点が過ぎた直後に死ぬ確率がハザード関数になります。
なので
\begin{eqnarray}
h(t)
&=& \frac{f(t)}{S(t)} \\
&=& \frac{-S^{'}(t)}{S(t)} \\
&=& \{-\log(S(t))\}^{'} \\
\end{eqnarray}
直感的に理解できますね。
\(t\)時点では生存していたのでその確率は\(S(t)\)
そしてその直後になくなってしまう確率は\(f(t)\)
よって、確率的には\(\displaystyle \frac{f(t)}{S(t)}\)になります。
\(S(t)\)は生存関数で生きてる確率なので\(1-S(t)\)は死んでいる確率。そして\(F(t)= 1-S(t)\)とする。
この時、微分して、\(F'(t) = f(t) = - S'(t)\)となる。
この\(f(t)\)は\(F(t)\)を微分したものなので、もちろん瞬間的に\(t\)時にて死んでしまう確率。
つまり、ハザード関数\(h(t)\)は\(h(t) = \displaystyle \frac{f(t)}{S(t)}\)がハザード関数となります。
ココがポイント
-
ハサード関数は、\(t\)時には生きていたけど、\(t\)時を過ぎた瞬間に亡くなってしまった時の関数
Cox比例ハザードモデル
cox比例ハザードモデルの定義である、
\begin{eqnarray}
h(t;X) &=& h_{0}(t)\exp(x^{T}\beta) \\
\end{eqnarray}
から
\begin{eqnarray}
h(t;X) &=& h_{0}(t)\exp(x^{T}\beta) \\
\log(h(t;X)) &=& \log(h_{0}(t)) + \log(\exp(x^{T}\beta)) \\
\log(h(t;X)) &=& \log(h_{0}(t)) + x^{T}\beta \\
\log(h(t;X)) - \log(h_{0}(t)) &=& x^{T}\beta \\
\log\frac{h(t;X)}{h_{0}(t)} &=& x^{T}\beta ・・・① \\
\frac{h(t;X)}{h_{0}(t)} &=& \exp(x^{T}\beta) \\
\end{eqnarray}
ここで\(①\)についてみると、ロジスティック回帰分析になっていることが確認できます。
右辺を見ると、説明変数と回帰係数の重み付けの和になっていて、左辺では対数を取っています。この形はロジスティック回帰の式と同じです。
\(\displaystyle \frac{h(t;X)}{h_{0}(t)}\)はハザード比になっていて、尚且つロジスティック回帰分析の観点で見れば、オッズ比になっていることもわかります。
\begin{eqnarray}
log(\frac{p}{1-p}) &=& x^{T}\beta \\
\end{eqnarray}
\(\displaystyle \frac{p}{1-p}\)の部分がロジスティック回帰のオッズ比になっている。\(p\)は確率。
ココがポイント
Cox比例ハザードモデルとは、ハザードモデルではそもそも時間tのみに依存した結果で、ただ単に表面上における結果を表したもので、実際にさまざまな要因が裏で及ぼした結果、イベントが起こったりしている。その要因も入れて分析するハザードモデルをCox比例ハザードモデルという。
ハザード関数の定義である、
\begin{eqnarray}
h(t;X) &=& - \frac{S^{'}(t;x)}{S(t;x)} = \{-\log(S(t;x))\}^{'} \\
\end{eqnarray}
から、この式をcox比例ハザードモデルの定義式に入れると、
\begin{eqnarray}
- \frac{S^{'}(t;x)}{S(t;x)} &=& - \frac{S^{'}_{0}(t;x)}{S_{0}(t;x)}\exp(x^{T}\beta) \\
\{\log(S(t;x))\}^{'} &=& \{\log(S_{0}(t;x))\}^{'}\exp(x^{T}\beta) \\
\log(S(t;x)) &=& \log(S_{0}(t;x))\exp(x^{T}\beta) \\
S(t;x) &=& S_{0}(t;x)^{\exp(x^{T}\beta)} \\
\end{eqnarray}
途中の\(\log\)の微分式に対して両辺を時間\(t\)で積分することで、\(\log(S(t;x))\)にしてます。
カプランマイヤーの2重対数を考える。
2つの生存関数を考える。
1つは薬A(=\(x\))を投与した時の生存関数で、
もう1つは薬B(=\(x^{*}\))を投与した時の生存関数とする。
この2つの差はどう表されるのかを考える。
\begin{eqnarray}
\frac{S(t;x)}{S(t;x^{*})} &=& \frac{S_{0}(t)^{\exp(x^{T}\beta)}}{S_{0}(t)^{\exp(x^{*T}\beta)}} \\
\end{eqnarray}
に対して、分母分子それぞれ対数を取って、
\begin{eqnarray}
\frac{\log(S(t;x))}{\log(S(t;x^{*}))} &=& \frac{\exp(x^{T}\beta) \cdot \log(S_{0}(t))}{\exp(x^{*T}\beta) \cdot \log(S_{0}(t))} \\
\frac{\log(S(t;x))}{\log(S(t;x^{*}))} &=& \exp((x-x^{*})^{T}\beta ) \\
\log\frac{\log(S(t;x))}{\log(S(t;x^{*}))} &=& (x-x^{*})^{T}\beta \\
\log\{\log(S(t;x))\} - \log\{\log(S(t;x^{*}))\} &=& (x-x^{*})^{T}\beta \\
\end{eqnarray}
これにより、2重対数で2つの説明変数があって、それぞれの影響度合いの差分を取ってみると、\((x-x^{*})^{T}\beta\)になってる。
\begin{eqnarray}
\frac{S(t;x)}{S(t;x^{*})} &=& \frac{S_{0}(t)^{\exp(x^{T}\beta)}}{S_{0}(t)^{\exp(x^{*T}\beta)}} \\
\end{eqnarray}
カプランマイヤー
打ち切りなどの情報整理
https://pharma-navi.bayer.jp/bayaspirin/imasara/medical-statistics/no5/a3
実際に生存関数を求めるのが難しい場合、カプランマイヤー曲線などを用いて分析することが可能です。
カプランマイヤー曲線は生存曲線と同じ意味で、何かイベントが下がると下がっていく曲線です。
生存関数でも各年齢ごとに人は亡くなっているので、どんどん右下に加工していく曲線になりますが、
カプランマイヤー曲線を作成するのに必要な表を作成します。
まず大事なこととしては、生存関数と同じなので、イベントが起きた情報が必要です。
カプランマイヤーは生存関数と同じ座標軸なので、
曲線を書く上で必要な情報としては、時間とイベントが起きた時間です。
ここで、\(n_{i}\)は時間\(i\)時点における残りの被験者の人数で、
\(d_{i}\)は時間\(i\)時点における打ち切りで検証対象外となった人数
\begin{eqnarray}
S(t) &=&
\left\{ \,
\begin{aligned}
& \prod_{i:t > t_{1}} 1 - \frac{d_{i}}{n_{i}} (t > t_{1}) \\
& 1 (t_{1} > t)
\end{aligned}
\right.
\end{eqnarray}
最初は、誰もイベントが起きていないので、確率は1になる。つまり\(S(0)=1\)です。
イベントが発生したら、一段下がる。
一段下がったタイミングでの確率
生存関数は滑らかな図になりますが、
カプランマイヤーは表にある情報を図にして曲線を描いていくので、カクカクになります。
ただ両方の仕組みは全く同じですし、スタートラインの0が確率1であることも同じだし、イベントが発生したらその分下がるのも一緒です。
なので、原理は一緒ですが、
生存関数は具体的な僕らが普段使っている確率密度関数をそのまま使用でき、カプランマイヤーは自分でプロットして作成するという点が違います!生存関数、具体的な曲線を求めれない場合にカプランマイヤーを考えるという形になります。
ココがポイント
- カプランマイヤー曲線は具体的な生存関数を求めれない時にグラフィカルに求める曲線のこと。
- 生存関数と性質は全く同じ。
\begin{eqnarray}
S(t_{j})
&=& S(t_{j-1}) \cdot P(T > t_{j}|T \geq t_{j})
\end{eqnarray}
| 生存時間(週):\(t_{j}\) | 打ち切りの有無(1:打ち切り、0:イベント) |
|---|---|
| 5 | 0 |
| 8 | 0 |
| 10 | 1 |
| 12 | 0 |
| 15 | 1 |
のデータが取れた時、これをカプランマイヤー生存関数を求めてみます。
\begin{eqnarray}
S(5) &=& 1 \\
S(8) &=& S(5)(\frac{4}{5}) = \frac{4}{5} \\
S(12) &=& S(8)(\frac{1}{2}) = \frac{2}{5} \\
\end{eqnarray}
この生存時間解析の概念は、いろんなところで使えそうですね!
生存関数は減少関数になるので、例えば記憶は日が経つごとにどんどん忘れていくので、忘却曲線は減少関数になります。
となると、どういった要因で記憶が下がっていくのかを分析するのに有用です。
どの段階で忘れてしまったかのイベントの定義は難しいですが、、