
層別サンプリングでは、
ある地域をMECEで層別にいくつかの層に分けます。
そしてそれぞれの層から上のようなことをします。
非復元であるので独立ではなく、上の解法で求める必要があります。
ある1つの層に着目をした上で、
その層での標本平均の期待値と分散を求めます。
\(x_{11},x_{12},...,x_{1 N_{1}}\)
\(x_{21},x_{22},...,x_{2 N_{2}}\)
\(x_{31},x_{32},...,x_{3 N_{3}}\)
\(x_{k1},x_{k2},...,x_{k N_{k}}\)
層別抽出法では、
層別で通常は有限母集団を考えます。
その中でいくつかの層(グループ)に分けて単純サンプリングを行うというものです。
人のサンプリングであれば同じ人をサンプリングすることはないので、非復元サンプリングになります。
Contents
層別サンプリング
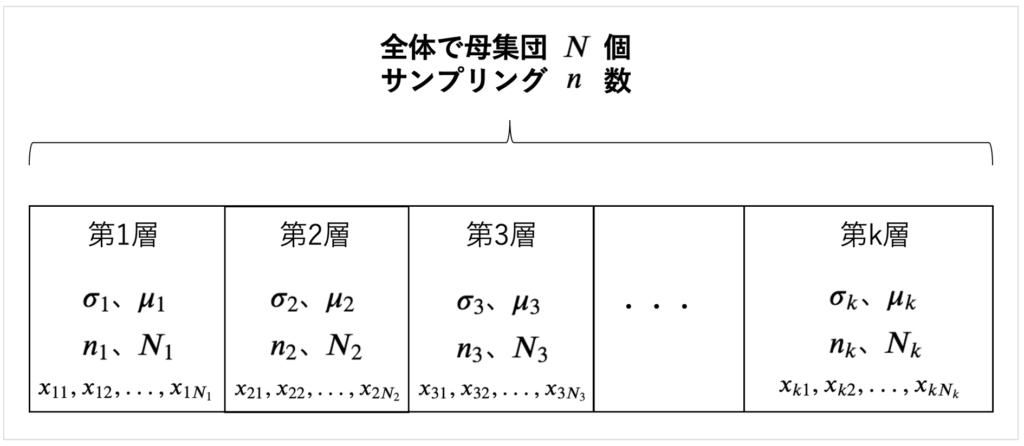
\( \sigma_{k}\)は第\(k\)層における標準偏差、
\( \mu_{k} \)は第\(k\)層における平均、
\( n_{k} \)は第\(k\)層における今回のサンプリング数、
\( N_{k} \)は第\(k\)層における母集団の数、
\( x_{k1},x_{k2},...,x_{k N_{k}} \)は第\(k\)層における全てのデータ(値)、
とします。
そしてサンプリングでは、母集団の平均を推測することが大事で、母集団の標本平均を求めてみましょう!
各層ごとの標本平均を出す
まず各層ごとの標本平均を出します。各層ごとに\(n_{k}\)個サンプリングするので、
\begin{eqnarray}
\bar{X_{k}}
&=& \displaystyle \frac{1}{n_{k}} \sum_{i=1}^{n_{k}} x_{k i}\\
\end{eqnarray}
このデータで平均値が出たので、この第\(k\)層における全データの数値は、\(k\)層では母集団\(N_{k}\)なので、\(N_{k}\)倍することで求めることができ、
\begin{eqnarray}
k層における総計
&=& k層のデータ数 \cdot k層の標本平均 \\
&=& N_{k} \cdot \bar{X_{k}} \\
&=& N_{k} \cdot \displaystyle \frac{1}{n_{k}} \sum_{i=1}^{n_{k}} x_{k i}\\
&=& \displaystyle \frac{N_{k}}{n_{k}} \sum_{i=1}^{n_{k}} x_{k i}\\
\end{eqnarray}
となります。
したがって、母集団全体における平均値は、
\begin{eqnarray}
母集団全体における平均値
&=& \displaystyle \frac{1}{N} \sum_{i=1}^{k} l層における総計 \\
&=& \displaystyle \frac{1}{N} \sum_{l=1}^{k} \frac{N_{l}}{n_{l}} \sum_{i=1}^{n_{k}} x_{k i} \\
&=& \displaystyle \sum_{l=1}^{k} \frac{N_{l}}{Nn_{l}} \sum_{i=1}^{n_{k}} x_{k i} \\
&=& \displaystyle \sum_{l=1}^{k} \pi_{l} \Bigr( \frac{1}{n_{l}} \sum_{i=1}^{n_{k}} x_{k i} \Bigr) \\
&=& \displaystyle \sum_{l=1}^{k} \pi_{l} \bar{X_{l}} \\
\end{eqnarray}
ここで、\(\displaystyle \pi_{l} = \frac{N_{l}}{N}\)とする。
標本平均\(\bar{X_{}}\)は、各層を\(k\)とした時、各層における標本平均を\(\bar{X_{k}}\)とした時、
\begin{eqnarray}
\bar{X_{}}
&=& \displaystyle \sum_{i=1}^{k} \pi_{k}\bar{X_{k}} \\
\end{eqnarray}
となります。
よって、各層からのサンプリングは独立であること、
そして、各層からのサンプリングは、母集団が\(N_{k}\)の有限母集団でそこから非復元サンプリングで\(n_{k}\)個をサンプリングするということは、単純な有限母集団の非復元サンプリングであるので、各層の標本平均の分散が、\(V(\bar{X_{k}}) = \displaystyle \frac{\sigma_{k}^{2}}{n_{k}} \Bigr( 1 - \frac{n_{k}-1}{N_{k}-1}\Bigr) \)であること
から
標本平均の分散\(V(\bar{X_{}})\)は、
\begin{eqnarray}
V(\bar{X_{}})
&=& V\Bigr(\sum_{i=1}^{k} \pi_{k}\bar{X_{k}}\Bigr) \\
&=& \pi_{1}^{2} V(\bar{X_{1}}) + \pi_{2}^{2} V(\bar{X_{2}}) + \pi_{3}^{2} V(\bar{X_{3}}) + \cdot\cdot\cdot + \pi_{n}^{2} V(\bar{X_{n}}) \\
&=& \pi_{1}^{2} \displaystyle \frac{\sigma_{1}^{2}}{n_{1}}\Bigr(\displaystyle \frac{N_{1}-n_{1}}{N_{1}-1} \Bigr) +
\pi_{2}^{2} \displaystyle \frac{\sigma_{2}^{2}}{n_{2}}\Bigr(\displaystyle \frac{N_{2}-n_{2}}{N_{2}-1} \Bigr) +
\pi_{3}^{2} \displaystyle \frac{\sigma_{3}^{2}}{n_{3}}\Bigr(\displaystyle \frac{N_{3}-n_{3}}{N_{3}-1} \Bigr) +
\cdot\cdot\cdot +
\pi_{n}^{2} \displaystyle \frac{\sigma_{n}^{2}}{n_{n}}\Bigr(\displaystyle \frac{N_{n}-n_{n}}{N_{n}-1} \Bigr) \\
&=& \sum_{k=1}^{n}\pi_{k}^{2}\cdot\displaystyle\frac{\sigma_{k}^{2}}{n_{k}}\Bigr(\displaystyle\frac{N_{k}-n_{k}}{N_{k}-1}\Bigr) \\
\end{eqnarray}
単純サンプリングと層別抽出法の比較
直感的にそれぞれのグループからいくつかをサンプリングするので、それぞれのグループの特徴をある程度反映したサンプリングができているので、それなりにサンプリングはうまく行ってそうな予感しますね!
ん?有限母集団で非復元サンプリング。。
以下のリンクで扱ってます!
直接有限母集団からいくつかサンプリングをした場合と、有限母集団をいくつかのグループに分けてそこからサンプリングする層別抽出法の場合ではどちらがよりいいサンプリングができるのかを考えていきましょう!!
これがポイントです!
さて、同じ有限母集団からの非復元サンプリング。
そのサンプリング方法が多少違いますが、条件は同じ。
どちらが良いサンプリングなのでしょうか?
比較するためにも、まずは層別抽出法での標本平均の期待値や分散を求めてみます!
(8.8)より\(N\)を\(\infty\)としたとき、
\begin{eqnarray}
\frac{1}{n} \sum_{i=1}^{k}\pi_{j}\sigma_{j}^{2} \cdot \frac{N_{j} - {n}}{N_{j} - 1}
&=& \frac{1}{n} \sum_{i=1}^{k}\pi_{j}\sigma_{j}^{2} \cdot \frac{1 - \displaystyle \frac{n}{N}}{1 - \displaystyle \frac{1}{N_{j}}} \\
&=& \frac{1}{n} \sum_{i=1}^{k}\pi_{j}\sigma_{j}^{2} \\
\end{eqnarray}
よって、
\(①\)有限母集団の非復元サンプリングにおける標本平均の分散と、
\(②\)有限母集団で複数の層に分けて、それぞれ\(n_{j}\)個を非復元サンプリングした際の標本平均の分散を比較して、
\begin{eqnarray}
① - ②
&=& \displaystyle \frac{\sigma^{2}}{n} - \displaystyle \frac{1}{n} \sum_{j=1}^{k}\pi_{j}\sigma_{j}^{2} \\
&=& \displaystyle \frac{1}{n} ( \sigma^{2} - \sum_{j=1}^{k} \pi_{j}\sigma_{j}^{2} ) \\
&=& \displaystyle \frac{1}{n} \sum_{j=1}^{k} \pi_{j}(\mu_{j}-\mu)^{2} \geq 0 \\
\end{eqnarray}
一番下は、層間分散と層内分散の違いから
\begin{eqnarray}
\sigma^{2} &=& \sum_{j=1}^{k} \pi_{j}\sigma_{j}^{2} + \sum_{j=1}^{k} \pi_{j}(\mu_{j}-\mu)^{2}
\end{eqnarray}
の法則を用いて変換しています。右辺の第1項は層内分散、右辺の第2項は層間分散です。
層内:層内のデータの分散なので通常の分散
層間:層を1つのデータとみなしたときの各層の間の距離(分散)
この結果から、
有限母集団の非復元サンプリングよりも、層別抽出法の方が良いサンプリングだということがわかりました!
ココがポイント
普通に母集団からサンプリング数を\(n\)個ときめて、母集団からサンプリングした場合と、層別抽出法のように層を切ってサンプリングをした方が、母平均のズレは小さくなる。
つまり層別抽出法の方が優れたサンプリング方法となる。
そもそもなぜ標本平均の分散が小さいといいのか?
サンプリングする際に母集団の中でも外れ値というか、変な部分をサンプリングして、母平均とそのサンプリングで得た標本平均が離れているとよくないです。
例えば、10回のうち4回くらいが母平均よりも離れてるくらいのサンプリング方法を作った時に、それでコスト的にも1回しか実施できないサンプリングを実施したときに母平均から離れてしまっては良くないです。
全数調査するわけではないので完全一致は無理ですが、できる限り母平均に近いようなサンプリングができることが望ましいです。
そして実際は母平均がどこにあるかはわからないので、分散が大きくなく、ある程度同じところに標本平均が固まれば大体そこら辺に母平均があるよねと判定できます。
なので標本平均の分散が小さいことが重要になるということです。
ココがポイント
サンプリングは1回のみ!その1回で求まった標本平均(母集団の予測値)を以下にして、母平均からずれていないかを目指すことが大事。
サンプルをとる手法を考える
上ではあくまで層別ごとにサンプルを取るという手法を構築しました!
そして普通の有限母集団から非復元サンプリングをした時よりも、分散が小さいので層別抽出法はいいサンプリングとは言えました!
ただ、じゃあ各層からはどのくらいの数のサンプル数\(n_{j}\)を取ればいいのでしょうか?
それを考えるために、以下3つのパターンを考えます!
- \(①\)【比例サンプリング法】各層ごとの数の比率に応じて、サンプル数を取得する
- \(②\)【等分配法】各層同じ数だけ、サンプルを取得する
- \(③\)【ネイマン配分法】全体の個数を一定にした上で、この層別抽出法の分散で最小となる各層のサンプリング数の組み合わせを求める
\(①\)比例サンプリング法
比例サンプリング法とは、各層の個数に応じて分配する方法です。
まず全体として\(n\)個サンプリングをすると決めている時に、各層の母数分で比例にサンプリングする方法で、
例えば、100個サンプリングをするとして、
今層が3つあり、A層の母集団は500個、B層は300個、C層は200個として全体の母集団は1000個としたとき、
A層の比率は0.5、B層は0.3、C層は0.2なので、
A層からは100*0.5 = 50個、
B層からは100*0.3 = 30個
C層からは100*0.2 = 20個
をそれぞれの層からサンプリングをするということになります。
これが比例サンプリング方になります。
\(②\) 等分配法
等分配法はその名の通り、各層からは同じ個数をサンプリングします。
全体のサンプリング数を\(N\)、層の数が\(l\)とすれば、
各層でのサンプリング数は\(\displaystyle \frac{N}{l}\)ということになります。
これは単純ですね!
サンプリング数を100個としたときに、層を4つとすれば、
各層からは100/4 = 25個をサンプリングするということになります。
\(③\)ネイマン配分法
\(n = \displaystyle \sum_{k=1}^{n} n_{k}\)と条件を定めた上でサンプリングをします。
サンプリングする総数は\(n\)で固定にしつつも、各層のサンプリングの数は変数にします。
なので、例えば、合計で100個をサンプリングするとした場合に、
層1:50個、層2:10個、層3:15個、層4:25個
層1:40個、層2:30個、層3:20個、層4:10個
というように、合計は100で固定にしつつも、各層のサンプリング数を変更して、数多あるパターンの中で一番標本平均の分散が小さくなるパターンを見つけるのが、ネイマン分配法と言います。
ラグランジュの未定乗数法を用いると、
\begin{eqnarray}
n_{j} &=& \frac{nN_{j}\sigma_{j} \sqrt{\displaystyle \frac{N_{j}}{N_{j}-1}} }{ \displaystyle \sum_{j=1}^{k} N_{j}\sigma_{j} \sqrt{\displaystyle \frac{N_{j}}{N_{j}-1}} }
\end{eqnarray}
となります。
\begin{eqnarray}
n_{j} &=& \frac{N_{j}\sigma_{j} \sqrt{\displaystyle \frac{N_{j}}{N_{j}-1}} }{ \displaystyle \sum_{j=1}^{k} N_{j}\sigma_{j} \sqrt{\displaystyle \frac{N_{j}}{N_{j}-1}} } \cdot n
\end{eqnarray}
なので、\(n_{1} + n_{2} + n_{3} + \cdot \cdot \cdot + n_{k} = n\)となります。
この\(n_{j}\)の導出は以下で扱います。
実際に標本平均の分散が最小となるサンプルサイズを求める
\(\displaystyle n=\sum_{j=1}^{k}n_{j}\)という条件のもと、標本平均の分散が最小となるような\(n_{j}\)を求めます。
これを求めるには、ラグランジュの未定乗数法を用います。
このラグランジュの未定乗数法は、ある条件のもとである値の最小値を求める手法で、
簡単に関数を作ってみると、
\begin{eqnarray}
L &=& 標本平均 - \lambda(条件式) \\
\end{eqnarray}
と表せて、\(\lambda\)はラグランジュ定数です。
これを実際に偏微分して計算をしていきます。
\begin{eqnarray}
L
&=& V(\bar{X}) - \lambda\Bigr(n-\sum_{j=1}^{k}n_{j}\Bigr) \\
&=& \sum_{j=1}^{k}\pi_{j}^{2}\cdot\frac{\sigma_{j}^{2}}{n_{j}}\cdot\frac{N_{j}-n_{j}}{N_{j}-1} - \lambda\Bigr(n-\sum_{j=1}^{k}n_{j}\Bigr) \\
&=& \sum_{j=1}^{k} \frac{\pi_{j}^{2}\sigma_{j}^{2}}{N_{j}-1}\Bigr(\frac{N_{j}}{n_{j}}-1\Bigr) -\lambda\Bigr(n-\sum_{j=1}^{k}n_{j}\Bigr) \\
\end{eqnarray}
となり、未定乗数法で分散が最小になる時を考える。
\begin{eqnarray}
\frac{\partial L}{\partial\lambda}
&=& n - \sum_{j=1}^{k}n_{j} \\
&=& 0
\end{eqnarray}
\(n_{j}\)について偏微分します。
積の微分法を用いて、
\begin{eqnarray}
\frac{\partial L}{\partial n_{j}}
&=& \frac{\pi_{j}^{2}\sigma_{j}^{2}}{N_{j}-1}\Bigr(-\frac{N_{j}}{n_{j}^{2}}\Bigr) -\lambda(0-1) \\
&=& 0
\end{eqnarray}
これを計算して、
\begin{eqnarray}
\frac{\pi_{j}^{2}\sigma_{j}^{2}}{N_{j}-1}\Bigr(-\frac{N_{j}}{n_{j}^{2}}\Bigr) -\lambda(0-1) &=& 0 \\
-\frac{N_{j}}{N_{j}-1} \cdot \frac{\pi_{j}^{2}\sigma_{j}^{2}}{n_{j}^{2}} -\lambda &=& 0 \\
\lambda &=& \frac{N_{j}}{N_{j}-1} \cdot \frac{\pi_{j}^{2}\sigma_{j}^{2}}{n_{j}^{2}} \\
\end{eqnarray}
ここから\(n_{j}\)について整理すると、
\begin{eqnarray}
n_{j}^{2}\lambda &=& \frac{N_{j}}{N_{j}-1} \pi_{j}^{2}\sigma_{j}^{2} \\
n_{j}^{2} &=& \frac{N_{j}}{N_{j}-1} \frac{1}{\lambda} \pi_{j}^{2}\sigma_{j}^{2} \\
n_{j} &=& \sqrt{ \frac{N_{j}}{N_{j}-1}} \sqrt{\frac{1}{\lambda}} \pi_{j}\sigma_{j} ・・・① \\
\end{eqnarray}
ここで、\(\displaystyle n=\sum_{j=1}^{k}n_{j}\)であることから、
\begin{eqnarray}
n &=& \sum_{j=1}^{k} \sqrt{ \frac{N_{j}}{N_{j}-1}} \sqrt{\frac{1}{\lambda}} \pi_{j}\sigma_{j} \\
\sqrt{\lambda}n &=& \sqrt{ \frac{N_{j}}{N_{j}-1}} \pi_{j}\sigma_{j} \\
\sqrt{\lambda} &=& \frac{1}{n} \sqrt{ \frac{N_{j}}{N_{j}-1}} \pi_{j}\sigma_{j} ・・・② \\
\end{eqnarray}
②を①に代入して、
\begin{eqnarray}
n_{j} &=& \sqrt{ \displaystyle \frac{N_{j}}{N_{j}-1}} \pi_{j}\sigma_{j} \cdot \frac{1} {\displaystyle \frac{1}{n} \sum_{j=1}^{k} \sqrt{ \frac{N_{j}}{ N_{j}-1}}\pi_{j}\sigma_{j} } \\
n_{j} &=& \frac{\displaystyle n\pi_{j}\sigma_{j} \sqrt{\frac{N_{j}}{N_{j}-1}}} {\displaystyle \sum_{j=1}^{k} \pi_{j}\sigma_{j} \sqrt{ \frac{N_{j}}{ N_{j}-1}}} \\
\end{eqnarray}
そしてここで、\(\pi_{j} = \displaystyle \frac{N_{j}}{N} \)であることから、
\begin{eqnarray}
n_{j} &=& \frac{\displaystyle nN_{j}\sigma_{j} \sqrt{\frac{N_{j}}{N_{j}-1}}} {\displaystyle \sum_{j=1}^{k} N_{j}\sigma_{j} \sqrt{ \frac{N_{j}}{ N_{j}-1}}} \\
\end{eqnarray}
となります。
考え方
今回各層から何個ずつサンプリングをすれば良いのかを求める必要があります。
その時の各層\(j\)のサンプリング数をそれぞれ\(n_{j}\)とします。
この時の全体の標本平均の分散を求める。
そして\(n_{j}\)の数値であったり、その\(n_{j}\)個のデータによっては標本平均の数値は変わる。つまり標本平均にばらつきがある。
なのでこの標本平均の分散をいかに小さくできるかが大事で、
一番小さくするときの\(n_{j}\)を求めることで、たとえ各層からどんな値を取っても決められた\(n_{j}\)個のみをサンプリングすれば、最小の分散で標本平均を求めることができるよー。となる。
ココがポイント
層別抽出法には主に3つのサンプリング数を決める方法が存在する。
- ① 比例サンプリング法:各層の母集団のデータ数に応じてサンプリング数を割り振る
- ② 等分配法:各層にて同じ数をサンプリングする
- ③ ネイマン配分法:標本分散が最小になる場合を考えて、各層からサンプリングをする